scipy.interpolate.

make_interp_spline

scipy.interpolate.make_interp_spline(x, y, k=3, t=None, bc_type=None, ось=0, check_finite=True)

Создать интерполирующий B-сплайн с указанной степенью и граничными условиями.

Параметры:

xarray_like, форма (n,)

Абсциссы.

yarray_like, форма (n, …)

Ординаты.

kint, необязательный

Степень B-сплайна. По умолчанию кубическая, k = 3.

tarray_like, форма (nt + k + 1,), опционально.

Узлы. Количество узлов должно соответствовать количеству точек данных и количеству производных на краях. В частности, nt - n должен равняться len(deriv_l) + len(deriv_r).

bc_type2-кортеж или None

Граничные условия. По умолчанию None, что означает автоматический выбор граничных условий. В противном случае это должен быть кортеж длины два, где первый элемент (deriv_l) устанавливает граничные условия в x[0] и второй элемент (deriv_r) устанавливает граничные условия в x[-1]. Каждый из них должен быть итерируемым объектом пар (order, value) который дает значения производных указанных порядков на заданном краю интервала интерполяции. Альтернативно, распознаются следующие строковые псевдонимы:

• "clamped": Первые производные на концах равны нулю. Это

  эквивалентно bc_type=([(1, 0.0)], [(1, 0.0)]).

• "natural": Вторые производные на концах равны нулю. Это эквивалентно bc_type=([(2, 0.0)], [(2, 0.0)]).

• "not-a-knot" (по умолчанию): Первый и второй сегменты - это один и тот же полином. Это эквивалентно наличию bc_type=None.

• "periodic": Значения и первая k-1 производные на концах эквивалентны.

осьint, необязательный

Ось интерполяции. По умолчанию 0.

check_finitebool, необязательно

Проверять ли, что входные массивы содержат только конечные числа. Отключение может повысить производительность, но может привести к проблемам (сбоям, незавершению), если входные данные содержат бесконечности или NaN. По умолчанию True.

Возвращает:

bBSpline object

A BSpline объект степени k и с узлами t.

Смотрите также

BSpline

базовый класс, представляющий объекты B-сплайнов

CubicSpline

кубический сплайн в полиномиальном базисе

make_lsq_spline

#7602

UnivariateSpline

обертка над процедурами подгонки сплайнов FITPACK

splrep

обертка над процедурами подгонки сплайнов FITPACK

Примеры

Попробуйте в вашем браузере!

Использовать кубическую интерполяцию на узлах Чебышёва:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> def cheb_nodes(N):
...     jj = 2.*np.arange(N) + 1
...     x = np.cos(np.pi * jj / 2 / N)[::-1]
...     return x

>>> x = cheb_nodes(20)
>>> y = np.sqrt(1 - x**2)

>>> from scipy.interpolate import BSpline, make_interp_spline
>>> b = make_interp_spline(x, y)
>>> np.allclose(b(x), y)
True

Обратите внимание, что по умолчанию используется кубический сплайн с граничным условием not-a-knot

>>> b.k
3

Здесь мы используем 'естественный' сплайн с нулевыми вторыми производными на краях:

>>> l, r = [(2, 0.0)], [(2, 0.0)]
>>> b_n = make_interp_spline(x, y, bc_type=(l, r))  # or, bc_type="natural"
>>> np.allclose(b_n(x), y)
True
>>> x0, x1 = x[0], x[-1]
>>> np.allclose([b_n(x0, 2), b_n(x1, 2)], [0, 0])
True

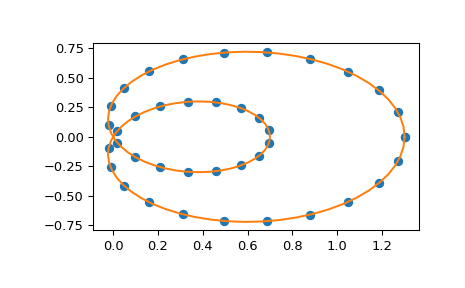
Также поддерживается интерполяция параметрических кривых. В качестве примера мы вычисляем дискретизацию спиральной кривой в полярных координатах

>>> phi = np.linspace(0, 2.*np.pi, 40)
>>> r = 0.3 + np.cos(phi)
>>> x, y = r*np.cos(phi), r*np.sin(phi)  # convert to Cartesian coordinates

Построить интерполяционную кривую, параметризуя её по углу

>>> spl = make_interp_spline(phi, np.c_[x, y])

Оценить интерполянт на более мелкой сетке (обратите внимание, что мы транспонируем результат, чтобы распаковать его в пару массивов x и y)

>>> phi_new = np.linspace(0, 2.*np.pi, 100)
>>> x_new, y_new = spl(phi_new).T

Построить результат

>>> plt.plot(x, y, 'o')
>>> plt.plot(x_new, y_new, '-')
>>> plt.show()

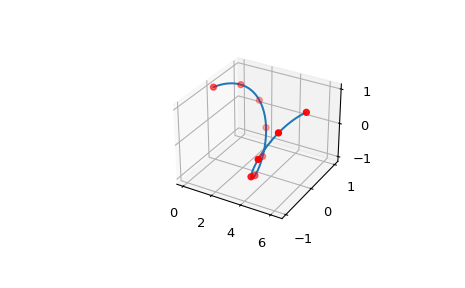
Построить B-сплайн кривую с двумерным y

>>> x = np.linspace(0, 2*np.pi, 10)
>>> y = np.array([np.sin(x), np.cos(x)])

Периодическое условие выполняется, потому что y-координаты точек на концах эквивалентны

>>> ax = plt.axes(projection='3d')
>>> xx = np.linspace(0, 2*np.pi, 100)
>>> bspl = make_interp_spline(x, y, k=5, bc_type='periodic', axis=1)
>>> ax.plot3D(xx, *bspl(xx))
>>> ax.scatter3D(x, *y, color='red')
>>> plt.show()

НазадОткрыть во вкладке