scipy.interpolate.

splrep#

scipy.interpolate.splrep(x, y, w=None, xb=None, xe=None, k=3, задача=0, s=None, t=None, full_output=0, на=0, quiet=1)[источник]#

Найти B-сплайн представление одномерной кривой.

Наследие

Эта функция считается устаревшей и больше не будет получать обновления. Хотя у нас в настоящее время нет планов по её удалению, мы рекомендуем, чтобы новый код использовал более современные альтернативы. В частности, мы рекомендуем использовать make_splrep в новом коде.

Для заданного набора точек данных (x[i], y[i]) определить гладкую сплайн-аппроксимацию степени k на интервале xb <= x <= xe.

Параметры:

x, yarray_like

Точки данных, определяющие кривую y = f(x).

warray_like, необязательный

Строго положительный массив весов ранга 1 той же длины, что и x и y. Веса используются при вычислении взвешенного сплайна методом наименьших квадратов. Если ошибки в y значения имеют стандартное отклонение, заданное вектором d, затем w должен быть 1/d. По умолчанию ones(len(x)).

xb, xefloat, опционально

Интервал для подгонки. Если None, по умолчанию используются x[0] и x[-1] соответственно.

kint, необязательный

Степень сплайн-аппроксимации. Рекомендуется использовать кубические сплайны. Чётные значения k следует избегать, особенно с малыми s значения. 1 <= k <= 5.

задача{1, 0, -1}, опционально

Если task==0, найти t и c для заданного коэффициента сглаживания, s.

Если task==1 найти t и c для другого значения коэффициента сглаживания, s. Должен был быть предыдущий вызов с task=0 или task=1 для того же набора данных (t будет сохранено и использовано внутри)

Если task=-1 найти взвешенный сплайн наименьших квадратов для заданного набора узлов, t. Это должны быть внутренние узлы, так как узлы на концах будут добавлены автоматически.

sfloat, опционально

Условие сглаживания. Степень гладкости определяется удовлетворением условий: sum((w * (y - g))**2,axis=0) <= s где g(x) является сглаженной интерполяцией (x,y). Пользователь может использовать s для управления компромиссом между близостью и гладкостью аппроксимации. Большие значения s означает большее сглаживание при меньших значениях s указывают на меньшее сглаживание. Рекомендуемые значения s зависят от весов, w. Если веса представляют обратное стандартное отклонение y, тогда хороший s значение должно находиться в диапазоне (m-sqrt(2*m),m+sqrt(2*m)) где m является количеством точек данных в x, y, и w. по умолчанию : s=m-sqrt(2*m) если веса предоставлены. s = 0.0 (интерполирующий), если веса не предоставлены.

tarray_like, необязательный

Узлы, необходимые для task=-1. Если задано, то задача автоматически устанавливается в -1.

full_outputbool, необязательно

Если не равно нулю, то возвращаются дополнительные выходные данные.

наbool, необязательно

Если ненулевое, точки данных считаются периодическими с периодом x[m-1] - x[0] и возвращается гладкое периодическое сплайн-приближение. Значения y[m-1] и w[m-1] не используются. По умолчанию ноль, что соответствует граничному условию 'not-a-knot'.

quietbool, необязательно

Ненулевое значение для подавления сообщений.

Возвращает:

tckкортеж: Кортеж (t,c,k) содержащий вектор узлов, коэффициенты B-сплайна и степень сплайна.
fpмассив, опционально: Взвешенная сумма квадратов невязок сплайн-аппроксимации.
ierint, необязательный: Целочисленный флаг об успехе splrep. Успех указывается, если ier<=0. Если ier in [1,2,3], произошла ошибка, но она не была вызвана. В противном случае ошибка вызывается.
msgstr, optional: Сообщение, соответствующее целочисленному флагу, ier.

Смотрите также

UnivariateSpline, BivariateSpline
splprep, splev, sproot, spalde, splint
bisplrep, bisplev
BSpline
make_interp_spline

Примечания

См. splev для оценки сплайна и его производных. Использует подпрограмму FORTRAN curfit из FITPACK.

Пользователь отвечает за обеспечение того, чтобы значения x уникальны. В противном случае, splrep не вернет осмысленных результатов.

Если предоставлены, узлы t должны удовлетворять условиям Шёнберга-Уитни, т.е. должно существовать подмножество точек данных x[j] такой, что t[j] < x[j] < t[j+k+1], для j=0, 1,...,n-k-2.

Эта подпрограмма дополняет нулями массив коэффициентов c иметь ту же длину, что и массив узлов t (замыкающий k + 1 коэффициенты игнорируются подпрограммами оценки, splev и BSpline.) Это контрастирует с splprep, который не дополняет коэффициенты нулями.

Условие границы по умолчанию - 'not-a-knot', т.е. первый и второй сегменты на конце кривой являются одним полиномом. Дополнительные граничные условия доступны в CubicSpline.

Ссылки

На основе алгоритмов, описанных в [1], [2], [3], и [4]:

[1]

P. Dierckx, «Алгоритм сглаживания, дифференцирования и интегрирования экспериментальных данных с использованием сплайн-функций», J.Comp.Appl.Maths 1 (1975) 165-184.

[2]

P. Dierckx, "A fast algorithm for smoothing data on a rectangular grid while using spline functions", SIAM J.Numer.Anal. 19 (1982) 1286-1304.

[3]

П. Диеркс, «Улучшенный алгоритм аппроксимации кривых сплайн-функциями», отчет tw54, кафедра компьютерных наук, К.У. Лёвен, 1981.

[4]

P. Dierckx, «Curve and surface fitting with splines», Monographs on Numerical Analysis, Oxford University Press, 1993.

Примеры

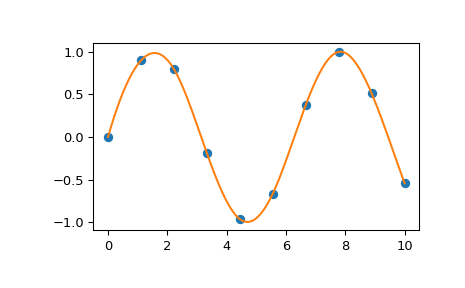
Вы можете интерполировать одномерные точки с помощью B-сплайновой кривой. Дополнительные примеры приведены в в учебнике.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import splev, splrep
>>> x = np.linspace(0, 10, 10)
>>> y = np.sin(x)
>>> spl = splrep(x, y)
>>> x2 = np.linspace(0, 10, 200)
>>> y2 = splev(x2, spl)
>>> plt.plot(x, y, 'o', x2, y2)
>>> plt.show()

../../_images/scipy-interpolate-splrep-1.png