scipy.interpolate.

InterpolatedUnivariateSpline

класс scipy.interpolate.InterpolatedUnivariateSpline(x, y, w=None, ограничивающая рамка=[None, None, k=3, расширение=0, check_finite=False)

1-D интерполирующий сплайн для заданного набора точек данных.

Наследие

Этот класс считается устаревшим и больше не будет получать обновления. Хотя в настоящее время у нас нет планов по его удалению, мы рекомендуем, чтобы новый код использовал более современные альтернативы. В частности, мы рекомендуем использовать make_interp_spline вместо этого.

Аппроксимирует сплайн y = spl(x) степени k к предоставленному x, y данные. Сплайн-функция проходит через все предоставленные точки. Эквивалентно UnivariateSpline с s = 0.

Параметры:

x(N,) array_like

Входная размерность точек данных — должна быть строго возрастающей

y(N,) array_like

входная размерность точек данных

w(N,) array_like, optional

Веса для аппроксимации сплайнами. Должны быть положительными. Если None (по умолчанию), все веса равны 1.

ограничивающая рамка(2,) array_like, необязательный

2-последовательность, задающая границы интервала аппроксимации. Если None (по умолчанию), bbox=[x[0], x[-1]].

kint, необязательный

Степень сглаживающего сплайна. Должна быть 1 <= k <= 5. По умолчанию k = 3, кубический сплайн.

расширениеint или str, необязательно

Управляет режимом экстраполяции для элементов, не находящихся в интервале, определенном последовательностью узлов.

• если ext=0 или 'extrapolate', вернуть экстраполированное значение.

• если ext=1 или ‘zeros’, вернуть 0

• если ext=2 или ‘raise’, вызвать ValueError

• если ext=3 для ‘const’, вернуть граничное значение.

Значение по умолчанию 0.

check_finitebool, необязательно

Проверять ли, что входные массивы содержат только конечные числа. Отключение может повысить производительность, но может привести к проблемам (сбоям, бесконечному выполнению или бессмысленным результатам), если входные данные содержат бесконечности или NaN. По умолчанию: False.

Методы

__call__(x[, nu, ext])	Вычислить сплайн (или его nu-ю производную) в позициях x.
antiderivative([n])	Создайте новый сплайн, представляющий первообразную этого сплайна.
derivative([n])	Создать новый сплайн, представляющий производную этого сплайна.
derivatives(x)	Вернуть все производные сплайна в точке x.
get_coeffs()	Вернуть коэффициенты сплайна.
get_knots()	Возвращает позиции внутренних узлов сплайна.
get_residual()	Вернуть взвешенную сумму квадратов остатков аппроксимации сплайном.
integral(a, b)	Возвращает определенный интеграл сплайна между двумя заданными точками.
roots()	Возвращает нули сплайна.
set_smoothing_factor(s)	Продолжить вычисление сплайна с заданным коэффициентом сглаживания s и узлами, найденными при последнем вызове.

validate_input

Смотрите также

UnivariateSpline

гладкий одномерный сплайн для аппроксимации заданного набора точек данных.

LSQUnivariateSpline

сплайн, для которого узлы выбираются пользователем

SmoothBivariateSpline

сглаживающий двумерный сплайн через заданные точки

LSQBivariateSpline

двумерный сплайн с использованием взвешенного метода наименьших квадратов

splrep

функция для нахождения B-сплайнового представления 1-D кривой

splev

функция для оценки B-сплайна или его производных

sproot

функция для нахождения корней кубического B-сплайна

splint

функция для вычисления определённого интеграла B-сплайна между двумя заданными точками

spalde

функция для вычисления всех производных B-сплайна

Примечания

Количество точек данных должно быть больше степени сплайна k.

Примеры

Попробуйте в вашем браузере!

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import InterpolatedUnivariateSpline
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)
>>> spl = InterpolatedUnivariateSpline(x, y)
>>> plt.plot(x, y, 'ro', ms=5)
>>> xs = np.linspace(-3, 3, 1000)
>>> plt.plot(xs, spl(xs), 'g', lw=3, alpha=0.7)
>>> plt.show()

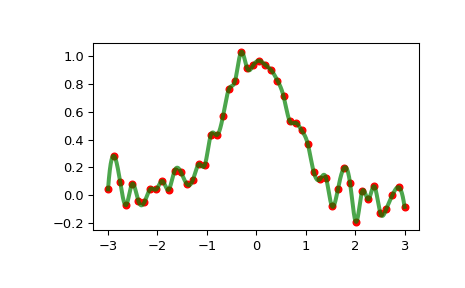
Обратите внимание, что spl(x) интерполирует y:

>>> spl.get_residual()
0.0

НазадОткрыть во вкладке