scipy.interpolate.

splprep#

scipy.interpolate.splprep(x, w=None, u=None, ub=None, ue=None, k=3, задача=0, s=None, t=None, full_output=0, nest=None, на=0, quiet=1)[источник]#

Найти B-сплайновое представление N-мерной кривой.

Наследие

Эта функция считается устаревшей и больше не будет получать обновления. Хотя у нас в настоящее время нет планов по её удалению, мы рекомендуем, чтобы новый код использовал более современные альтернативы. В частности, мы рекомендуем использовать make_splprep в новом коде.

Для списка из N массивов ранга 1, x, которые представляют кривую в N-мерном пространстве, параметризованную u, найти гладкую аппроксимирующую сплайн-кривую g(u). Использует подпрограмму FORTRAN parcur из FITPACK.

Параметры:

xarray_like: Список массивов векторов-выборок, представляющих кривую.
warray_like, необязательный: Строго положительный массив весов ранга 1 той же длины, что и x[0]. Веса используются при вычислении взвешенного сплайна методом наименьших квадратов. Если ошибки в x значения имеют стандартное отклонение, заданное вектором d, тогда w должно быть 1/d. По умолчанию ones(len(x[0])).
uarray_like, необязательный: Массив значений параметров. Если не задан, эти значения рассчитываются автоматически как M = len(x[0]), где

v[0] = 0

v[i] = v[i-1] + distance(x[i], x[i-1])

u[i] = v[i] / v[M-1]
ub, ueint, необязательный: Конечные точки интервала параметров. По умолчанию u[0] и u[-1].
kint, необязательный: Степень сплайна. Рекомендуются кубические сплайны. Чётные значения k следует избегать, особенно с малым значением s. 1 <= k <= 5, по умолчанию 3.
задачаint, необязательный: Если task==0 (по умолчанию), найти t и c для заданного коэффициента сглаживания s. Если task==1, найти t и c для другого значения коэффициента сглаживания s. Должен быть предыдущий вызов с task=0 или task=1 для того же набора данных. Если task=-1, найти взвешенный сплайн наименьших квадратов для заданного набора узлов t.
sfloat, опционально: Условие сглаживания. Степень гладкости определяется удовлетворением условий: sum((w * (y - g))**2,axis=0) <= s, где g(x) — сглаженная интерполяция (x,y). Пользователь может использовать s для управления компромиссом между точностью и гладкостью аппроксимации. Большие s означает большее сглаживание, в то время как меньшие значения s указывают на меньшее сглаживание. Рекомендуемые значения s зависят от весов, w. Если веса представляют обратную величину стандартного отклонения y, то хороший s значение должно находиться в диапазоне (m-sqrt(2*m),m+sqrt(2*m)), где m — количество точек данных в x, y и w.
tмассив, опционально: Узлы, необходимые для task=-1. Должно быть как минимум 2*k+2 узлы.
full_outputint, необязательный: Если не равно нулю, то возвращаются дополнительные выходные данные.
nestint, необязательный: Завышенная оценка общего числа узлов сплайна для помощи в определении требуемого объёма памяти. По умолчанию nest=m/2. Всегда достаточно большой является nest=m+k+1.
наint, необязательный: Если ненулевое, точки данных считаются периодическими с периодом x[m-1] - x[0] и возвращается гладкая периодическая сплайн-аппроксимация. Значения y[m-1] и w[m-1] не используются.
quietint, необязательный: Ненулевое значение для подавления сообщений.

Возвращает:

tckкортеж: Кортеж, (t,c,k) содержащий вектор узлов, коэффициенты B-сплайна и степень сплайна.
uмассив: Массив значений параметра.
fpfloat: Взвешенная сумма квадратов невязок сплайн-аппроксимации.
ierint: Целочисленный флаг об успехе splrep. Успех указывается, если ier<=0. Если ier в [1,2,3], произошла ошибка, но она не была вызвана. В противном случае ошибка вызывается.
msgstr: Сообщение, соответствующее целочисленному флагу ier.

Смотрите также

splrep, splev, sproot, spalde, splint
bisplrep, bisplev
UnivariateSpline, BivariateSpline
BSpline
make_interp_spline

Примечания

См. splev для вычисления сплайна и его производных. Количество измерений N должно быть меньше 11.

Количество коэффициентов в c массив является k+1 меньше, чем количество узлов, len(t). Это контрастирует с splrep, который дополняет нулями массив коэффициентов, чтобы он имел ту же длину, что и массив узлов. Эти дополнительные коэффициенты игнорируются процедурами вычисления, splev и BSpline.

Ссылки

[1]

P. Dierckx, "Algorithms for smoothing data with periodic and parametric splines, Computer Graphics and Image Processing", 20 (1982) 171-184.

[2]

P. Dierckx, "Algorithms for smoothing data with periodic and parametric splines", report tw55, Dept. Computer Science, K.U.Leuven, 1981.

[3]

P. Dierckx, «Curve and surface fitting with splines», Monographs on Numerical Analysis, Oxford University Press, 1993.

Примеры

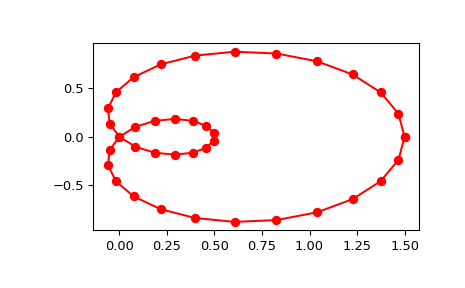
Сгенерировать дискретизацию кривой улитки Паскаля в полярных координатах:

>>> import numpy as np
>>> phi = np.linspace(0, 2.*np.pi, 40)
>>> r = 0.5 + np.cos(phi)         # polar coords
>>> x, y = r * np.cos(phi), r * np.sin(phi)    # convert to cartesian

И интерполировать:

>>> from scipy.interpolate import splprep, splev
>>> tck, u = splprep([x, y], s=0)
>>> new_points = splev(u, tck)

Обратите внимание, что (i) мы принудительно используем интерполяцию, применяя s=0, (ii) параметризация, u, генерируется автоматически. Теперь постройте результат:

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> ax.plot(x, y, 'ro')
>>> ax.plot(new_points[0], new_points[1], 'r-')
>>> plt.show()

../../_images/scipy-interpolate-splprep-1.png