scipy.special.

jnp_zeros

scipy.special.jnp_zeros(n, nt)

Вычислить нули производных функций Бесселя целого порядка Jn'.

Вычислить nt нули функций \(J_n'(x)\) на интервале \((0, \infty)\). Нули возвращаются в возрастающем порядке. Обратите внимание, что этот интервал исключает ноль в \(x = 0\) который существует для \(n > 1\).

Параметры:

nint

Порядок функции Бесселя

ntint

Количество нулей для возврата

Возвращает:

ndarray

First nt нули функции Бесселя.

Смотрите также

jvp

Производные целочисленного порядка функций Бесселя первого рода

jv

Функции Бесселя первого рода дробного порядка

Ссылки

[1]

Zhang, Shanjie and Jin, Jianming. “Computation of Special Functions”, John Wiley and Sons, 1996, chapter 5. https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html

Примеры

Попробуйте в вашем браузере!

Вычислить первые четыре корня \(J_2'\).

>>> from scipy.special import jnp_zeros
>>> jnp_zeros(2, 4)
array([ 3.05423693,  6.70613319,  9.96946782, 13.17037086])

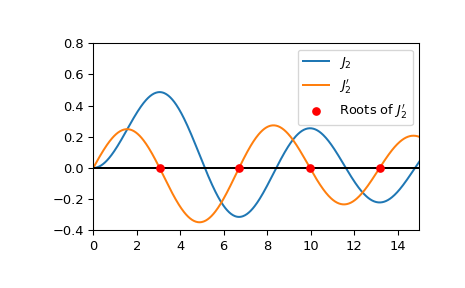
Поскольку jnp_zeros дает корни \(J_n'\), его можно использовать для вычисления местоположений пиков функции \(J_n\). График \(J_2\), \(J_2'\) и местоположения корней \(J_2'\).

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.special import jn, jnp_zeros, jvp
>>> j2_roots = jnp_zeros(2, 4)
>>> xmax = 15
>>> x = np.linspace(0, xmax, 500)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, jn(2, x), label=r'$J_2$')
>>> ax.plot(x, jvp(2, x, 1), label=r"$J_2'$")
>>> ax.hlines(0, 0, xmax, color='k')
>>> ax.scatter(j2_roots, np.zeros((4, )), s=30, c='r',
...            label=r"Roots of $J_2'$", zorder=5)
>>> ax.set_ylim(-0.4, 0.8)
>>> ax.set_xlim(0, xmax)
>>> plt.legend()
>>> plt.show()

НазадОткрыть во вкладке