scipy.stats.

Биномиальное#

класс scipy.stats.Биномиальное(*, n, p, **kwargs)[источник]#

Биномиальное распределение с заданной вероятностью успеха и количеством испытаний

Функция плотности вероятности биномиального распределения:

\[f(x) = {n \choose x} p^x (1 - p)^{n-x}\]

для \(x \in \{0, 1, ..., n - 1, n\}\). Этот класс принимает одну параметризацию: n для \(n \in \{0, 1, 2, ...\}\), p для \(p \in (0, 1)\).

Параметры:
tolположительное число с плавающей точкой, опционально

Желаемая относительная погрешность вычислений. Если не указана, вычисления могут быть быстрее; при указании вычисления могут с большей вероятностью достичь желаемой точности.

validation_policy{None, "skip_all"}

Определяет уровень проверки входных данных для выполнения. Если не указано, проверка входных данных выполняется для обеспечения соответствующего поведения в пограничных случаях (например, параметры вне области определения, аргумент вне поддержки распределения и т.д.) и улучшения согласованности выходного dtype, формы и т.д. Передайте 'skip_all' чтобы избежать вычислительных затрат на эти проверки, когда допустимы грубые края.

cache_policy{None, "no_cache"}

Определяет степень кэширования промежуточных результатов. Если оставить неопределённым, промежуточные результаты некоторых вычислений (например, носитель распределения, моменты и т.д.) кэшируются для повышения производительности будущих вычислений. Передайте 'no_cache' для уменьшения памяти, зарезервированной экземпляром класса.

Атрибуты:
Все параметры доступны как атрибуты.

Методы

support()

Носитель случайной величины

plot([x, y, t, ax])

Построить график функции распределения.

sample([shape, method, rng])

Случайная выборка из распределения.

moment([order, kind, method])

Сырой, центральный или стандартный момент положительного целого порядка.

mean(*[, method])

Среднее (сырой первый момент относительно начала координат)

median(*[, method])

Медиана (50-й процентиль)

mode(*[, method])

Мода (наиболее вероятное значение)

variance(*[, method])

Дисперсия (центральный момент второго порядка)

standard_deviation(*[, method])

Стандартное отклонение (квадратный корень из второго центрального момента)

skewness(*[, method])

Асимметрия (стандартизированный третий момент)

kurtosis(*[, method, convention])

Эксцесс (стандартизированный четвертый момент)

pdf(x, /, *[, method])

Функция плотности вероятности

logpdf(x, /, *[, method])

Логарифм функции плотности вероятности

cdf(x[, y, method])

Функция кумулятивного распределения

icdf(p, /, *[, method])

Обратная функция распределения.

ccdf(x[, y, method])

Дополнительная функция распределения

iccdf(p, /, *[, method])

Обратная дополнительная кумулятивная функция распределения.

logcdf(x[, y, method])

Логарифм функции кумулятивного распределения

ilogcdf(logp, /, *[, method])

Обратная функция логарифма кумулятивной функции распределения.

logccdf(x[, y, method])

Логарифм дополнительной кумулятивной функции распределения

ilogccdf(logp, /, *[, method])

Обратная функция логарифма дополнительной функции распределения.

entropy(*[, method])

Дифференциальная энтропия

logentropy(*[, method])

Логарифм дифференциальной энтропии

Смотрите также

Руководство по переходу для случайных величин

Учебник

Примечания

В документации используются следующие сокращения.

  • PDF: функция плотности вероятности

  • CDF: функция распределения

  • CCDF: дополнительная функция распределения

  • энтропия: дифференциальная энтропия

  • log-F: логарифм F (например, log-CDF)

  • обратный F: обратная функция к F (например, обратная функция распределения)

Документация API написана для описания API, а не для использования в качестве статистической справки. Усилия направлены на то, чтобы быть корректными на уровне, необходимом для использования функциональности, а не на математическую строгость. Например, непрерывность и дифференцируемость могут подразумеваться неявно. Для точных математических определений обратитесь к предпочитаемому математическому тексту.

Примеры

Чтобы использовать класс распределения, его необходимо создать с использованием ключевых параметров, соответствующих одной из принятых параметризаций.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> from scipy.stats import Binomial
>>> X = Binomial(n=10.0, p=0.34)

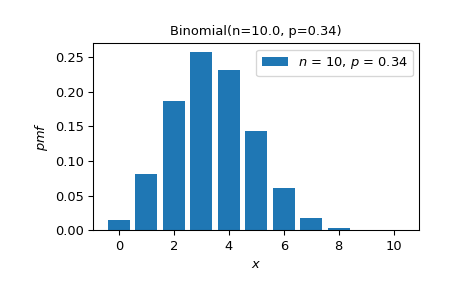
Для удобства, plot метод может использоваться для визуализации плотности и других функций распределения.

>>> X.plot()
>>> plt.show()
../../_images/scipy-stats-Binomial-1_00_00.png

Носитель базового распределения доступен с использованием support метод.

>>> X.support()
(np.float64(0.0), np.float64(10.0))

Числовые значения параметров, связанных со всеми параметризациями, доступны как атрибуты.

>>> X.n, X.p
(np.float64(10.0), np.float64(0.34))

Для вычисления функции плотности вероятности/массы базового распределения в аргументе x=3.0:

>>> x = 3.0
>>> X.pdf(x), X.pmf(x)
(np.float64(inf), np.float64(0.2572915634331659))

Интегральная функция распределения, её дополнение и логарифм этих функций вычисляются аналогично.

>>> np.allclose(np.exp(X.logccdf(x)), 1 - X.cdf(x))
True

Существуют методы для вычисления мер центральной тенденции, дисперсии, моментов высшего порядка и энтропии.

>>> X.mean(), X.median(), X.mode()
(np.float64(3.4000000000000004), np.float64(3.0), np.float64(3.0))

>>> X.variance(), X.standard_deviation()
(np.float64(2.2439999999999998), np.float64(1.4979986648859203))

>>> X.skewness(), X.kurtosis()
(np.float64(0.21361834793382106), np.float64(2.845632798573975))

>>> np.allclose(X.moment(order=6, kind='standardized'),
...             X.moment(order=6, kind='central') / X.variance()**3)
True

>>> X.entropy()
1.816303869320522

Псевдослучайные выборки могут быть извлечены из базового распределения с использованием sample.

>>> X.sample(shape=(4,))
array([2., 4., 1., 4.])  # may vary
На этой странице