Открыть как блокнот

Руководство по переходу для случайных величин

Фон

До SciPy 1.15 все непрерывные распределения вероятностей SciPy (например, scipy.stats.norm) были экземплярами подклассов scipy.stats.rv_continuous.

from scipy import stats
dist = stats.norm
type(dist)

scipy.stats._continuous_distns.norm_gen

isinstance(dist, stats.rv_continuous)

True

Существовало два очевидных способа работы с этими объектами.

Согласно более распространённому подходу, оба "аргумента" (например, x) и «параметры распределения» (например, loc, scale) были предоставлены в качестве входных данных для методов объекта.

x, loc, scale = 1., 0., 1.
dist.pdf(x, loc, scale)

np.float64(0.24197072451914337)

Менее распространённый подход заключался в вызове __call__ метод объекта распределения, который возвращал экземпляр rv_continuous_frozen, независимо от исходного класса.

frozen = stats.norm()
type(frozen)

scipy.stats._distn_infrastructure.rv_continuous_frozen

Методы этого нового объекта принимают только аргументы, а не параметры распределения.

frozen.pdf(x)

np.float64(0.24197072451914337)

В некотором смысле, экземпляры rv_continuous как norm представляли «семейства распределений», которые требуют параметров для идентификации конкретного распределения вероятностей, и экземпляр rv_continuous_frozen был похож на "случайную величину" - математический объект, который следует определенному вероятностному распределению.

Оба подхода допустимы и имеют преимущества в определенных ситуациях. Например, stats.norm.pdf(x) выглядит более естественным, чем stats.norm().pdf(x) для такого простого вызова или когда методы рассматриваются как функции параметров распределения, а не обычных аргументов (например, правдоподобия). Однако первый подход имеет несколько присущих недостатков; например, все 125 непрерывных распределений SciPy должны быть созданы при импорте, параметры распределения должны проверяться каждый раз при вызове метода, а документация методов должна либо а) генерироваться отдельно для каждого метода каждого распределения, либо б) опускать параметры формы, уникальные для каждого распределения. Чтобы устранить эти и другие недостатки, gh-15928 предложил новую, отдельную инфраструктуру на основе последнего (случайная величина) подхода. Это руководство по переходу документирует, как пользователи rv_continuous и rv_continuous_frozen может перейти на новую инфраструктуру.

Примечание: Новая инфраструктура может пока не быть столь удобной для некоторых случаев использования, особенно для подбора параметров распределения к данным. Пользователи могут продолжать использовать старую инфраструктуру, если она соответствует их потребностям; на данный момент она не устарела.

Основы

В новой инфраструктуре семейства распределений являются классами, названными в соответствии с CamelCase соглашения. Они должны быть созданы перед использованием, с параметрами, передаваемыми как аргументы только по ключевым словам. Экземпляры классы семейств распределений можно рассматривать как случайные величины, которые в математике обычно обозначаются заглавными буквами.

from scipy import stats
mu, sigma = 0, 1
X = stats.Normal(mu=mu, sigma=sigma)
X

Normal(mu=np.float64(0.0), sigma=np.float64(1.0))

После создания параметры формы можно читать (но не записывать) как атрибуты.

X.mu, X.sigma

(np.float64(0.0), np.float64(1.0))

Документация scipy.stats.Normal содержит ссылки на подробную документацию каждого из своих методов. (Сравните, например, с документацией scipy.stats.norm.)

Примечание: Хотя только Normal и Uniform имеют отрендеренную документацию и могут быть импортированы напрямую из stats начиная с SciPy 1.15, почти все другие старые распределения могут использоваться с новым интерфейсом через make_distribution (обсуждается далее).

Методы затем вызываются путем передачи только аргумента(ов), если они есть, без параметров распределения.

X.mean()

np.float64(0.0)

X.pdf(x)

np.float64(0.24197072451914337)

Для простых вызовов, подобных этому (например, аргумент является допустимым float), вызовы методов новых случайных переменных обычно будут быстрее, чем сравнимые вызовы старых методов распределений.

%timeit X.pdf(x)

2.36 μs ± 17.5 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

%timeit frozen.pdf(x)

17 μs ± 285 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

%timeit dist.pdf(x, loc=mu, scale=sigma)

17 μs ± 83 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

Обратите внимание, что способ X.pdf и frozen.pdf n_observations dist.pdf очень похож — единственное отличие заключается в вызове dist.pdf включает параметры формы, тогда как в новой инфраструктуре параметры формы предоставляются только при создании случайной величины.

Кроме того pdf и mean, несколько других методов новой инфраструктуры по сути такие же, как старые методы.

• logpdf (логарифм функции плотности вероятности)

• cdf (функция распределения)

• logcdf (логарифм функции распределения)

• entropy (дифференциальная энтропия)

• median

• support

Другие методы имеют новые названия, но в остальном являются прямыми заменами.

• sf (функция выживания) \(\rightarrow\) ccdf (дополнительная функция распределения)

• logsf \(\rightarrow\) logccdf

• ppf (функция процентной точки) \(\rightarrow\) icdf (обратная функция распределения)

• isf (обратная функция выживания) \(\rightarrow\) iccdf (обратная дополнительная кумулятивная функция распределения)

• std \(\rightarrow\) standard_deviation

• var \(\rightarrow\) variance

Новая инфраструктура имеет несколько новый методы в том же духе, что и выше.

• ilogcdf (обратная функция логарифма функции распределения)

• ilogccdf (обратная функция логарифма дополнительной функции распределения)

• logentropy (логарифм энтропии)

• mode (мода распределения)

• skewness

• kurtosis (не избыточный эксцесс; см. “Стандартизированные моменты” ниже)

И у него есть новый plot метод для удобства

import matplotlib.pyplot as plt
X.plot()
plt.show()

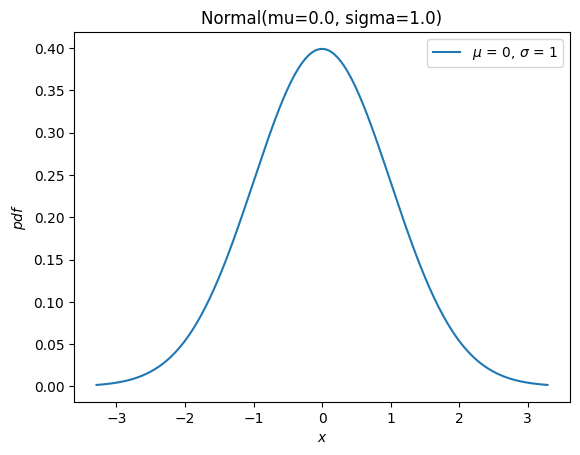
Большинство оставшихся методов старой инфраструктуры (rvs, moment, stats, interval, fit, nnlf, fit_loc_scale, и expect) имеют аналогичную функциональность, но требуется некоторая осторожность. Прежде чем описывать замены, кратко упомянем, как работать со случайными величинами, не распределенными нормально: почти все старые объекты распределений могут быть преобразованы в новый класс распределения с помощью scipy.stats.make_distribution, и новый класс распределения может быть создан путем передачи параметров формы как ключевых аргументов. Например, рассмотрим Распределение Вейбулла. Мы можем создать новый класс, который является абстракцией семейства распределений, например:

Weibull = stats.make_distribution(stats.weibull_min)
print(Weibull.__doc__[:288])  # help(Weibull) prints this and (too much) more

This class represents `scipy.stats.weibull_min` as a subclass of ``.
The `repr`/`str` of class instances is `Weibull`.
The PDF of the distribution is defined for :math:`x \in [0.0, \infty]`.
This class accepts one p

Согласно документации weibull_min, параметр формы обозначается c, поэтому мы можем создать случайную величину, передав c в качестве аргумента ключевого слова для нового Weibull класс.

c = 2.
X = Weibull(c=c)
X.plot()
plt.show()

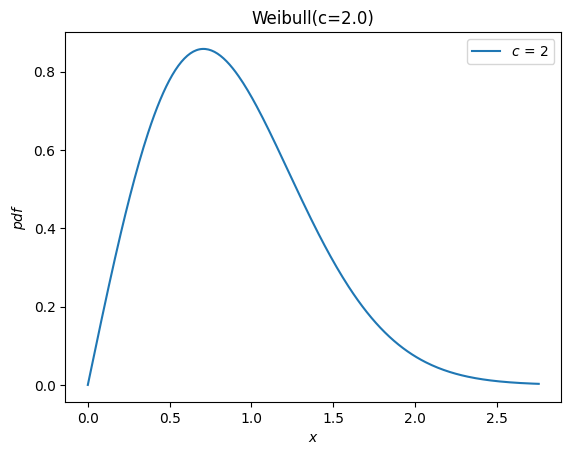
Ранее все распределения наследовали loc и scale параметры распределения. Эти параметры больше не принимаются. Вместо этого случайные величины можно сдвигать и масштабировать с помощью арифметических операторов.

Y = 2*X + 1
Y.plot()  # note the change in the abscissae
plt.show()

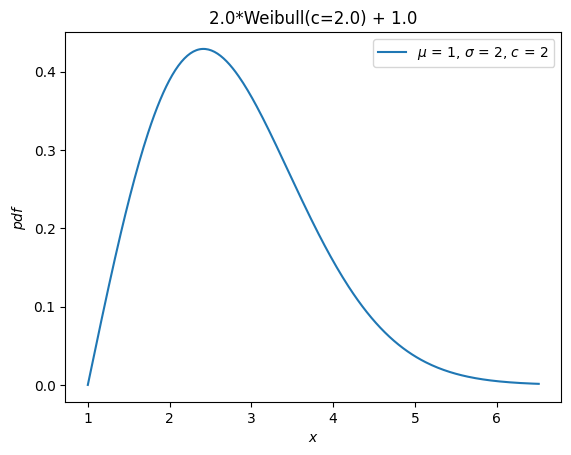
Отдельное распределение, weibull_max, был предоставлен как отражение weibull_min относительно начала координат. Теперь это просто -X.

Y = -X
Y.plot()
plt.show()

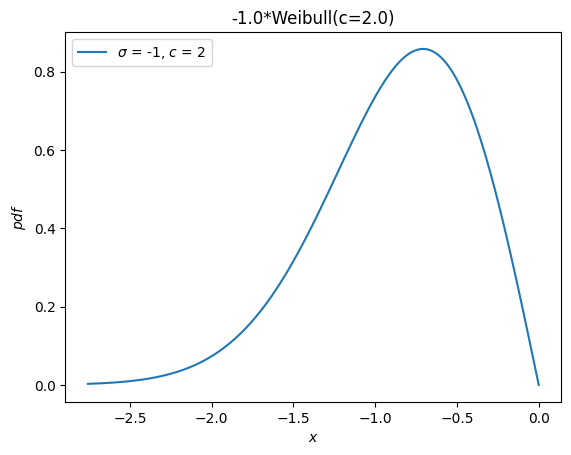
Моменты

Старая инфраструктура предлагает moments метод для сырых моментов. Когда указан только порядок, новый moment метод является прямой заменой.

stats.weibull_min.moment(1, c), X.moment(1)  # first raw moment of the Weibull distribution with shape c

(np.float64(0.8862269254527579), np.float64(0.8862269254527579))

Однако старая инфраструктура также имеет stats метод, который предоставлял различные статистики распределения. Следующие статистики были связаны с указанными символами.

• Среднее (первый начальный момент относительно начала координат, 'm')

• Дисперсия (второй центральный момент, 'v')

• Асимметрия (третий стандартизированный момент, 's')

• Эксцесс (четвертый стандартизированный момент минус 3, 'k')

Например:

stats.weibull_min.stats(c, moments='mvsk')

(np.float64(0.8862269254527579),
 np.float64(0.21460183660255183),
 np.float64(0.6311106578189344),
 np.float64(0.24508930068764556))

Теперь, моменты любого order и kind (сырые, центральные и стандартизированные) могут быть вычислены путем передачи соответствующих аргументов в новый moment метод.

(X.moment(order=1, kind='raw'), 
 X.moment(order=2, kind='central'), 
 X.moment(order=3, kind='standardized'), 
 X.moment(order=4, kind='standardized'))

(np.float64(0.8862269254527579),
 np.float64(0.21460183660255183),
 np.float64(0.6311106578189344),
 np.float64(3.2450893006876314))

Обратите внимание на разницу в определении куртозис. Ранее предоставлялся 'избыточный' (также известный как 'коэффициент эксцесса Фишера') эксцесс. В соответствии с соглашением (а не естественным математическим определением), это стандартизированный четвёртый момент, сдвинутый на постоянное значение (3) чтобы дать значение 0.0 для нормального распределения.

stats.norm.stats(moments='k')

np.float64(0.0)

Новый moment и kurtosis методы по умолчанию не следуют этому соглашению; они сообщают стандартизированный четвёртый момент согласно математическому определению. Это также известно как «неизбыточный» (или «пирсоновский») эксцесс, и для стандартного нормального распределения он имеет значение 3.0.

stats.Normal().moment(4, kind='standardized') 

np.float64(3.0)

Для удобства, kurtosis метод предлагает convention аргумент для выбора между двумя.

stats.Normal().kurtosis(convention='excess'), stats.Normal().kurtosis(convention='non-excess')

(np.float64(0.0), np.float64(3.0))

Случайные величины

Устаревшая инфраструктура rvs метод был заменён на sample, но есть два различия, которые следует отметить, когда требуется либо 1) контроль случайного состояния, либо 2) массивы используются для параметров формы, местоположения или масштаба.

Во-первых, аргумент random_state заменяется на rng на SPEC 7. Ранее для управления случайным состоянием использовался шаблон numpy.random.seed или передавать целочисленные сиды в random_state аргумент. Целочисленные сиды были преобразованы в экземпляры numpy.random.RandomState, поэтому поведение для заданного целочисленного сида будет идентичным в этих двух случаях:

import numpy as np
np.random.seed(1)
dist = stats.norm
dist.rvs(), dist.rvs(random_state=1)

(np.float64(1.6243453636632417), np.float64(1.6243453636632417))

В новой инфраструктуре передавайте экземпляры numpy.Generator в rng аргумент sample для управления случайным состоянием. Обратите внимание, что целочисленные сиды теперь преобразуются в экземпляры numpy.random.Generator, не экземпляры numpy.random.RandomState.

X = stats.Normal()
rng = np.random.default_rng(1)  # instantiate a numpy.random.Generator
X.sample(rng=rng), X.sample(rng=1)

(np.float64(0.345584192064786), np.float64(0.345584192064786))

Во-вторых, аргумент shape заменяет аргумент size.

dist.rvs(size=(3, 4))

array([[-0.61175641, -0.52817175, -1.07296862,  0.86540763],
       [-2.3015387 ,  1.74481176, -0.7612069 ,  0.3190391 ],
       [-0.24937038,  1.46210794, -2.06014071, -0.3224172 ]])

X.sample(shape=(3, 4))

array([[ 0.95340298,  1.47706056,  0.63413378,  0.86724603],
       [ 1.43211058,  1.16722574,  0.13904458,  1.93404904],
       [-2.37317063, -0.10882349,  1.25663928,  1.77189543]])

Помимо различия в названии, существует различие в поведении при работе с параметрами формы массива. Ранее форма массивов параметров распределения должна была включаться в size.

dist.rvs(size=(3, 4, 2), loc=[0, 1]).shape  # `loc` has shape (2,)

(3, 4, 2)

Теперь форма массивов параметров считается свойством самого объекта случайной величины. Указание формы параметров формы массива было бы избыточным, поэтому оно не включается при указании shape выборки.

Y = stats.Normal(mu = [0, 1])
Y.sample(shape=(3, 4)).shape  # the sample has shape (3, 4); each element is of shape (2,)

(3, 4, 2)

Интервалы вероятностной массы (также известные как "доверительные")

Старая инфраструктура предлагала interval метод, который по умолчанию возвращает симметричный (относительно медианы) интервал, содержащий заданный процент вероятностной массы распределения.

a = 0.95
dist.interval(confidence=a)

(np.float64(-1.959963984540054), np.float64(1.959963984540054))

Теперь вызовите методы обратной функции распределения и дополнительной функции распределения с желаемой вероятностной массой в каждом хвосте.

p = 1 - a
X.icdf(p/2), X.iccdf(p/2)

(np.float64(-1.959963984540054), np.float64(1.959963984540054))

Функция правдоподобия

Старая инфраструктура предлагает функцию для вычисления negative log-lправдоподобие function, ошибочно названный nnlf (вместо nllf). Он принимает параметры распределения как кортеж и наблюдения как массив.

mu = 0
sigma = 1
data = stats.norm.rvs(size=100, loc=mu, scale=sigma)
stats.norm.nnlf((mu, sigma), data)

np.float64(131.07116392314364)

Теперь просто вычислите отрицательное логарифмическое правдоподобие согласно его математическому определению.

X = stats.Normal(mu=mu, sigma=sigma)
-X.logpdf(data).sum()

np.float64(131.07116392314364)

Ожидаемые значения

The expect метод старой инфраструктуры оценивает определенный интеграл произвольной функции, взвешенной PDF распределения. Например, четвертый момент распределения задается как:

def f(x): return x**4
stats.norm.expect(f, lb=-np.inf, ub=np.inf)

np.float64(3.000000000000001)

Это обеспечивает небольшую дополнительную удобность по сравнению с тем, что делает исходный код: используйте scipy.integrate.quad для выполнения численного интегрирования.

from scipy import integrate
def f(x): return x**4 * stats.norm.pdf(x)
integrate.quad(f, a=-np.inf, b=np.inf)  # integral estimate, estimate of the error

(3.0000000000000053, 1.2043244026618655e-08)

Конечно, это можно так же легко сделать с помощью новой инфраструктуры.

def f(x): return x**4 * X.pdf(x)
integrate.quad(f, a=-np.inf, b=np.inf)  # integral estimate, estimate of the error

(3.0000000000000053, 1.2043244043338238e-08)

The conditional аргумент просто масштабирует результат на обратную величину вероятностной массы, содержащейся в интервале.

a, b = -1, 3
def f(x): return x**4
stats.norm.expect(f, lb=a, ub=b, conditional=True)

np.float64(1.657813862143119)

Используя quad непосредственно, то есть:

def f(x): return x**4 * stats.norm.pdf(x)
prob = stats.norm.cdf(b) - stats.norm.cdf(a)
integrate.quad(f, a=a, b=b)[0] / prob

np.float64(1.6578138621431193)

И с новыми случайными величинами:

integrate.quad(f, a=a, b=b)[0] / X.cdf(a, b)

np.float64(1.6578138621431193)

Обратите внимание, что cdf метод новых случайных величин принимает два аргумента для вычисления вероятностной массы в указанном интервале. Во многих случаях это позволяет избежать вычитательной ошибки («катастрофической потери точности»), когда вероятностная масса очень мала.

Обучение

Оценка местоположения / масштаба

Старая инфраструктура предлагала функцию для оценки параметров положения и масштаба распределения из данных.

rng = np.random.default_rng(91392794601852341588152500276639671056)
dist = stats.weibull_min
c, loc, scale = 0.5, 0, 4.
data = dist.rvs(size=100, c=c, loc=loc, scale=scale, random_state=rng)
dist.fit_loc_scale(data, c)
# compare against 0 (default location) and 4 (specified scale)

(np.float64(1.8268432669973347), np.float64(1.9640905288934327))

На основе исходного кода легко воспроизвести метод.

X = Weibull(c=c)
def fit_loc_scale(X, data):
    m, v = X.mean(), X.variance()
    m_, v_ = data.mean(), data.var()
    scale = np.sqrt(v_ / v)
    loc = m_ - scale*m
    return loc, scale

fit_loc_scale(X, data)

(np.float64(1.8268432669973347), np.float64(1.9640905288934327))

Обратите внимание, что оценки в этом примере довольно плохие, и низкая производительность эвристики повлияла на решение не предоставлять замену.

Метод максимального правдоподобия

Последний метод старой инфраструктуры — это fit, который оценивает параметры местоположения, масштаба и формы базового распределения по выборке из распределения.

c_, loc_, scale_ = stats.weibull_min.fit(data)
c_, loc_, scale_

(np.float64(0.5960699537061247),
 np.float64(1.8950104942593064e-05),
 np.float64(4.015875612107546))

Удобство этого метода — это и благословение, и проклятие.

Когда это работает, простота очень ценится. Для некоторых распределений аналитические выражения для оценки максимального правдоподобия (MLE) параметров были запрограммированы вручную, и для этих распределений fit метод довольно надежен.

Однако для большинства распределений подгонка выполняется путем численной минимизации функции отрицательного логарифма правдоподобия. Это не гарантирует успеха — как из-за внутренних ограничений MLE, так и из-за состояния искусства численной оптимизации — и в этих случаях пользователь fit застрял. Однако небольшое понимание значительно помогает обеспечить успех, поэтому здесь мы представляем мини-руководство по подгонке с использованием новой инфраструктуры.

Во-первых, обратите внимание, что ММП (метод максимального правдоподобия) — это одна из нескольких возможных стратегий подгонки распределений к данным. Он лишь находит значения параметров распределения, при которых минимизируется отрицательная логарифмическая функция правдоподобия (NLLF). Заметьте, что для распределения, из которого были сгенерированы данные, NLLF равна:

stats.weibull_min.nnlf((c, loc, scale), data)

np.float64(246.9503871545133)

NLLF параметров, оценённых с использованием fit ниже:

stats.weibull_min.nnlf((c_, loc_, scale_), data)

np.float64(230.35385152369787)

Следовательно, fit считает свою работу выполненной, независимо от того, удовлетворяет ли это представлениям пользователя о «хорошем соответствии» или находятся ли параметры в разумных пределах. Помимо возможности указать предположение для параметров распределения, он предоставляет мало контроля над процессом. (Примечание: технически, optimizer аргумент может использоваться для большего контроля, но это плохо документировано, и его использование сводит на нет любое удобство, предлагаемое fit метод.)

Другая проблема заключается в том, что метод максимального правдоподобия (MLE) по своей природе плохо себя ведет для некоторых распределений. В этом примере, например, мы можем сделать NLLF сколь угодно низким, просто установив параметр location в минимум данных - даже для фиктивных значений параметров shape и scale.

stats.weibull_min.nnlf((0.1, np.min(data), 10), data)

np.float64(-inf)

Усугубляя эти проблемы, то, что fit оценивает все параметры распределения по умолчанию, включая местоположение. В приведенном выше примере нас, вероятно, интересует только более распространенное двухпараметрическое распределение Вейбулла, поскольку фактическое местоположение равно нулю. fit может учесть это, указав, что местоположение является фиксированным параметром.

# c_, loc_, scale_ = stats.weibull_min.fit(data, loc=0)  # careful! this provides loc=0 as a *guess*
c_, loc_, scale_ = stats.weibull_min.fit(data, floc=0)
c_, loc_, scale_

(np.float64(0.5834128280886433), 0, np.float64(3.829972848420729))

stats.weibull_min.nnlf((c_, loc_, scale_), data)

np.float64(244.9617429249505)

Но, предоставив fit метод, который якобы «просто работает», побуждает пользователей пренебрегать некоторыми важными деталями.

Вместо этого мы предлагаем, что подгонка распределений к данным с использованием общих инструментов оптимизации, предоставляемых SciPy, почти так же проста. Однако это позволяет пользователю выполнять подгонку в соответствии с предпочтительной целевой функцией, предоставляет варианты, когда что-то идет не так, как ожидалось, и помогает пользователю избежать наиболее распространенных ошибок.

Например, предположим, что наша целевая функция действительно является отрицательным логарифмом правдоподобия. Её легко определить как функцию параметра формы c и масштаб только, оставляя местоположение по умолчанию равным нулю.

def nllf(x):
    c, scale = x  # pass (only) `c` and `scale` as elements of `x`
    X = Weibull(c=c) * scale
    return -X.logpdf(data).sum()

nllf((c_, scale_))

np.float64(244.96174292495053)

Для выполнения минимизации мы можем использовать scipy.optimize.minimize.

from scipy import optimize
eps = 1e-10  # numerical tolerance to avoid invalid parameters
lb = [eps, eps]  # lower bound on `c` and `scale`
ub = [10, 10]  # upper bound on `c` and `scale`
x0 = [1, 1]  # guess to get optimization started
bounds = optimize.Bounds(lb, ub)
res_mle = optimize.minimize(nllf, x0, bounds=bounds)
res_mle

  message: CONVERGENCE: NORM OF PROJECTED GRADIENT <= PGTOL
  success: True
   status: 0
      fun: 244.96174292277675
        x: [ 5.834e-01  3.830e+00]
      nit: 13
      jac: [ 5.684e-06  0.000e+00]
     nfev: 45
     njev: 15
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>

Значение целевой функции практически идентично, и PDF-файлы неразличимы.

import matplotlib.pyplot as plt
x = np.linspace(eps, 15, 300)

c_, scale_ = res_mle.x
X = Weibull(c=c_)*scale_
plt.plot(x, X.pdf(x), '-', label='numerical optimization')

c_, _, scale_ = stats.weibull_min.fit(data, floc=0)
Y = Weibull(c=c_)*scale_
plt.plot(x, Y.pdf(x), '--', label='`weibull_min.fit`')

plt.hist(data, bins=np.linspace(0, 20, 30), density=True, alpha=0.1)
plt.xlabel('x')
plt.ylabel('pdf(x)')
plt.legend()
plt.ylim(0, 0.5)
plt.show()

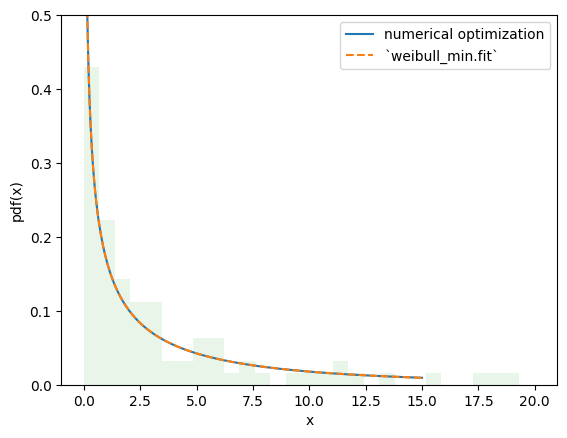
Однако с этим подходом легко вносить изменения в процедуру подгонки в соответствии с нашими потребностями, позволяя использовать процедуры оценки, отличные от предоставленных rv_continuous.fit. Например, мы можем выполнить оценки максимального интервала (MSE) путём изменения целевой функции на negative log product sтемп следующим образом.

def nlps(x):
    c, scale = x
    X = Weibull(c=c) * scale
    x = np.sort(np.concatenate((data, X.support())))  # Append the endpoints of the support to the data
    return -X.logcdf(x[:-1], x[1:]).sum().real  # Minimize the sum of the logs the probability mass between points

res_mps = optimize.minimize(nlps, x0, bounds=bounds)
res_mps.x

array([0.5591792 , 3.85552363])

Для метода L-моменты (который пытается сопоставить распределение и выборочные L-моменты):

def lmoment_residual(x):
    c, scale = x
    X = Weibull(c=c) * scale
    E11 = stats.order_statistic(X, r=1, n=1).mean()
    E12, E22 = stats.order_statistic(X, r=[1, 2], n=2).mean()
    lmoments_X = [E11, 0.5*(E22 - E12)]  # the first two l-moments of the distribution
    lmoments_x = stats.lmoment(data, order=[1, 2])  # first two l-moments of the data
    return np.linalg.norm(lmoments_x - lmoments_X)  # Minimize the norm of the difference

x0 = [0.4, 3]  # This method is a bit sensitive to the initial guess
res_lmom = optimize.minimize(lmoment_residual, x0, bounds=bounds)
res_lmom.x, res_lmom.fun  # residual should be ~0

(array([0.60943275, 3.90234501]), np.float64(5.041000173121575e-07))

Графики для всех трех методов выглядят схоже и, кажется, описывают данные, что дает нам некоторую уверенность в хорошем соответствии.

import matplotlib.pyplot as plt
x = np.linspace(eps, 10, 300)

for res, label in [(res_mle, "MLE"), (res_mps, "MPS"), (res_lmom, "L-moments")]:
    c_, scale_ = res.x
    X = Weibull(c=c_)*scale_
    plt.plot(x, X.pdf(x), '-', label=label)

plt.hist(data, bins=np.linspace(0, 10, 30), density=True, alpha=0.1)
plt.xlabel('x')
plt.ylabel('pdf(x)')
plt.legend()
plt.ylim(0, 0.3)
plt.show()

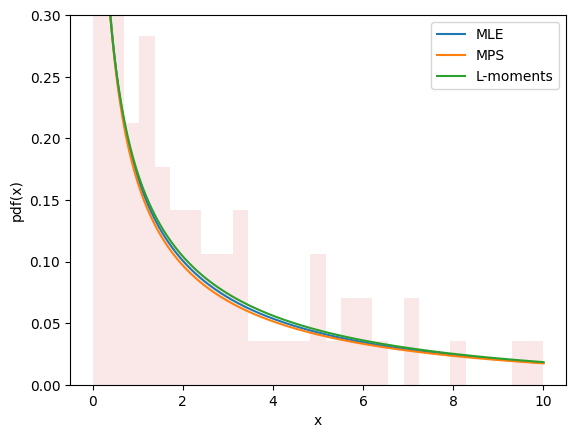
Оценка не всегда включает подгонку распределений к данным. Например, в gh-12134, пользователю нужно было вычислить параметры формы и масштаба распределения Вейбулла для достижения заданного среднего значения и стандартного отклонения. Это легко вписывается в ту же структуру.

moments_0 = np.asarray([8, 20])  # desired mean and standard deviation
def f(x):
    c, scale = x
    X = Weibull(c=c) * scale
    moments_X = X.mean(), X.standard_deviation()
    return np.linalg.norm(moments_X - moments_0)

bounds.lb = np.asarray([0.1, 0.1])  # the Weibull distribution is problematic for very small c
res = optimize.minimize(f, x0, bounds=bounds, method='slsqp')  # easily change the minimization method
res

     message: Optimization terminated successfully
     success: True
      status: 0
         fun: 4.594829312984325e-07
           x: [ 4.627e-01  3.430e+00]
         nit: 21
         jac: [ 1.322e+02 -2.330e-01]
        nfev: 100
        njev: 21
 multipliers: []

Новые и продвинутые возможности

Преобразования

К случайным величинам можно применять математические преобразования. Например, многие элементарные арифметические операции (+, -, *, /, **) между случайными величинами и скалярами работают.

Например, мы видим, что обратная величина к распределенной по Вейбуллу случайной величине распределена согласно scipy.stats.invweibull. («Обратное» распределение обычно является распределением, лежащим в основе обратной величины случайной величины.)

c = 10.6

X = Weibull(c=10.6)  
Y = 1 / X  # compare to `invweibull`
Y.plot()

x = np.linspace(0.8, 2.05, 300)
plt.plot(x, stats.invweibull(c=c).pdf(x), '--')
plt.legend(['`1 / X`', '`invweibull`'])
plt.title("Inverse Weibull PDF")
plt.show()

/home/treddy/github_projects/scipy/doc/build/env/lib/python3.11/site-packages/scipy/stats/_distribution_infrastructure.py:1966: RuntimeWarning: divide by zero encountered in divide
  h=lambda u: 1 / u, dh=lambda u: 1 / u ** 2)
/home/treddy/github_projects/scipy/doc/build/env/lib/python3.11/site-packages/scipy/stats/_continuous_distns.py:2750: RuntimeWarning: invalid value encountered in multiply
  return c*pow(x, c-1)*np.exp(-pow(x, c))

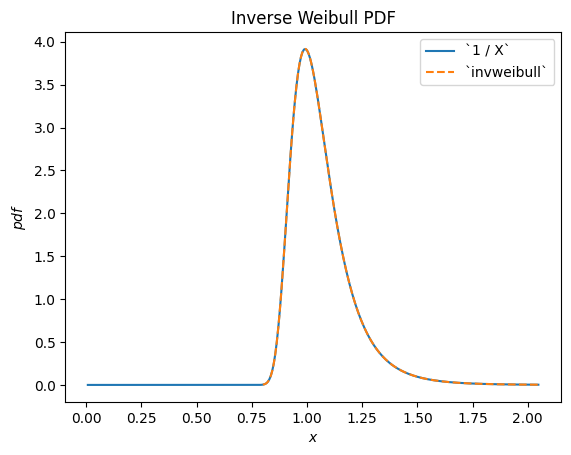
scipy.stats.chi2 описывает сумму квадратов нормально распределенных случайных величин.

X = stats.Normal()
Y = X**2  # compare to chi2
Y.plot(t=('x', eps, 5));

x = np.linspace(eps, 5, 300)
plt.plot(x, stats.chi2(df=1).pdf(x), '--')
plt.ylim(0, 3)
plt.legend(['`X**2`', '`chi2`'])
plt.title("Chi-squared PDF")
plt.show()

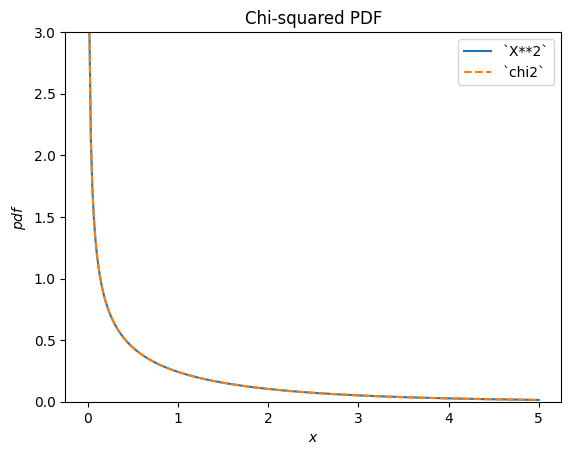
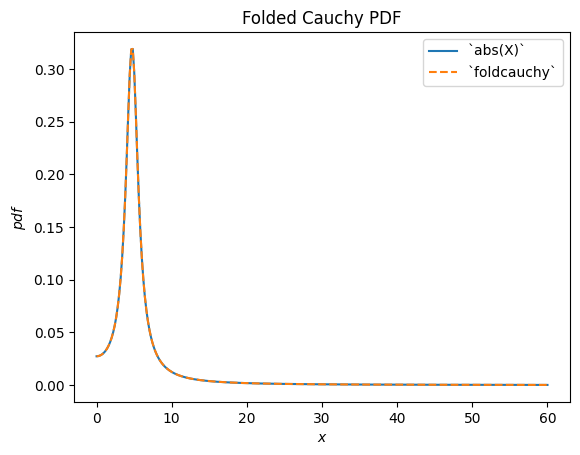
scipy.stats.foldcauchy описывает абсолютное значение случайной величины, распределенной по Коши. («Свернутое» распределение — это распределение, лежащее в основе абсолютного значения случайной величины.)

Cauchy = stats.make_distribution(stats.cauchy)
c = 4.72

X = Cauchy() + c  
Y = abs(X)  # compare to `foldcauchy`
Y.plot(t=('x', 0, 60))

x = np.linspace(0, 60, 300)
plt.plot(x, stats.foldcauchy(c=c).pdf(x), '--')
plt.legend(['`abs(X)`', '`foldcauchy`'])
plt.title("Folded Cauchy PDF")
plt.show()

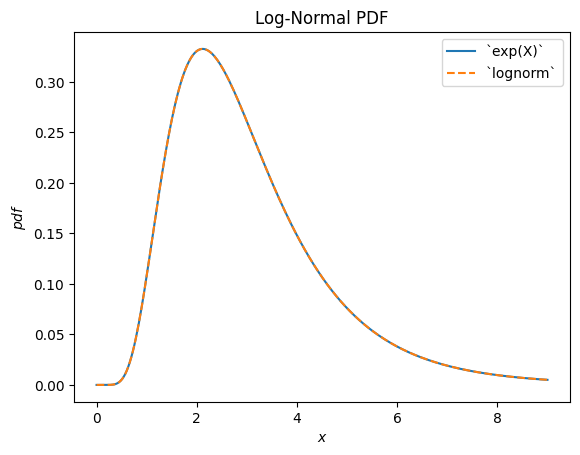
scipy.stats.lognormal описывает экспоненту нормально распределённой случайной величины. Название происходит от того, что логарифм результирующей случайной величины распределён нормально. (В общем случае «лог»-распределение обычно является распределением, лежащим в основе экспоненциальный случайной величины.)

u, s = 1, 0.5

X = stats.Normal()*s + u
Y = stats.exp(X)  # compare to `lognorm`
Y.plot(t=('x', eps, 9))

x = np.linspace(eps, 9, 300)
plt.plot(x, stats.lognorm(s=s, scale=np.exp(u)).pdf(x), '--')
plt.legend(['`exp(X)`', '`lognorm`'])
plt.title("Log-Normal PDF")
plt.show()

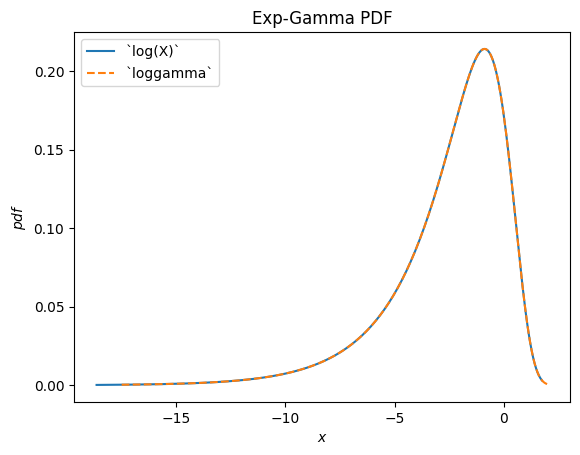
scipy.stats.loggamma описывает логарифм гамма-распределенной случайной величины. Обратите внимание, что согласно типичным соглашениям, подходящим названием этого распределения было бы exp-gamma потому что экспонента случайной величины распределена по гамма-распределению.

Gamma = stats.make_distribution(stats.gamma)
a = 0.414

X = Gamma(a=a)  
Y = stats.log(X)  # compare to `loggamma`
Y.plot()

x = np.linspace(-17.5, 2, 300)
plt.plot(x, stats.loggamma(c=a).pdf(x), '--')
plt.legend(['`log(X)`', '`loggamma`'])
plt.title("Exp-Gamma PDF")
plt.show()

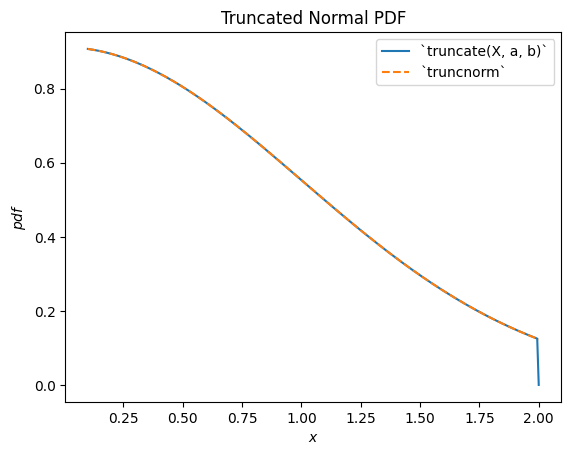
scipy.stats.truncnorm является распределением, лежащим в основе усеченной нормальной случайной величины. Обратите внимание, что преобразование усечения может быть применено либо до, либо после сдвига и масштабирования нормально распределенной случайной величины, что может значительно упростить достижение желаемого результата по сравнению с scipy.stats.truncnorm (что по своей сути сдвигает и масштабирует после усечение).

a, b = 0.1, 2

X = stats.Normal()  
Y = stats.truncate(X, a, b)  # compare to `truncnorm`
Y.plot()

x = np.linspace(a, b, 300)
plt.plot(x, stats.truncnorm(a, b).pdf(x), '--')
plt.legend(['`truncate(X, a, b)`', '`truncnorm`'])
plt.title("Truncated Normal PDF")
plt.show()

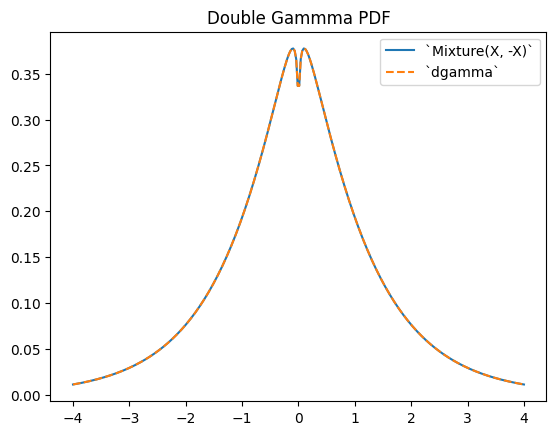
scipy.stats.dgamma является смесью двух гамма-распределённых случайных величин, одна из которых отражена относительно начала координат. (Обычно «двойное» распределение — это распределение, лежащее в основе смеси случайных величин, одна из которых отражена.)

a = 1.1
X = Gamma(a=a)
Y = stats.Mixture((X, -X), weights=[0.5, 0.5])
# plot method not available for mixtures

x = np.linspace(-4, 4, 300)
plt.plot(x, Y.pdf(x))
plt.plot(x, stats.dgamma(a=a).pdf(x), '--')
plt.legend(['`Mixture(X, -X)`', '`dgamma`'])
plt.title("Double Gammma PDF")
plt.show()

Ограничения

Хотя большинство арифметических преобразований между случайными величинами и скалярами Python или массивами NumPy поддерживаются, есть несколько ограничений.

• Возведение случайной величины в степень аргумента реализовано только когда аргумент является положительным целым числом.

• Возведение аргумента в степень случайной величины реализовано только тогда, когда аргумент является положительным скаляром, отличным от 1.

• Деление на случайную величину реализовано только тогда, когда носитель распределения либо полностью неотрицательный, либо неположительный.

• Логарифм случайной величины реализован только при неотрицательной области значений. (Логарифм отрицательных значений является мнимым.)

Арифметические операции между двумя случайными величинами не еще не поддерживается. Обратите внимание, что такие операции математически гораздо сложнее; например, PDF суммы двух случайных величин включает свертку двух PDF.

Также, хотя преобразования композируемы, а) усечение и б) сдвиг/масштабирование могут быть выполнены только один раз. Например, Y = 2 * stats.exp(X + 1) вызовет ошибку, так как это потребует сдвига перед возведением в степень и масштабирования после возведения в степень; это рассматривается как «сдвиг/масштабирование» дважды. Однако здесь (и во многих случаях) возможна математическая упрощение, чтобы избежать проблемы: Y = (2*math.exp(2)) * stats.exp(X) эквивалентно и требует только одной операции масштабирования.

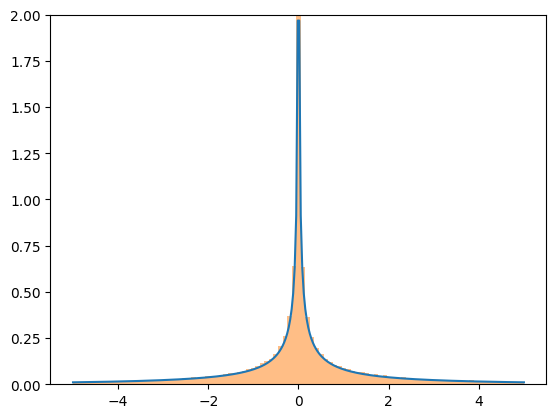
Хотя преобразования довольно устойчивы, все они полагаются на общие реализации, которые могут вызывать численные трудности. Если вас беспокоит точность результатов преобразования, рассмотрите сравнение полученной PDF с гистограммой случайной выборки.

X = stats.Normal()
Y = X**3
x = np.linspace(-5, 5, 300)
plt.plot(x, Y.pdf(x), label='pdf')
plt.hist(X.sample(100000)**3, density=True, bins=np.linspace(-5, 5, 100), alpha=0.5);
plt.ylim(0, 2)
plt.show()

Квази-Монте-Карло выборка

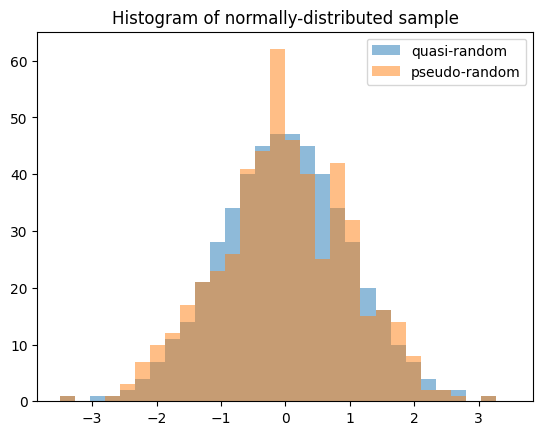
Случайные величины позволяют генерировать квазислучайные, низкодисперсные выборки из статистических распределений.

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
X = stats.Normal()

rng = np.random.default_rng(7824387278234)
qrng = stats.qmc.Sobol(1, rng=rng)  # instantiate a QMCEngine

bins = np.linspace(-3.5, 3.5, 31)
plt.hist(X.sample(512, rng=qrng), bins, alpha=0.5, label='quasi-random')
plt.hist(X.sample(512, rng=rng), bins, alpha=0.5, label='pseudo-random')
plt.title('Histogram of normally-distributed sample')
plt.legend()
plt.show()

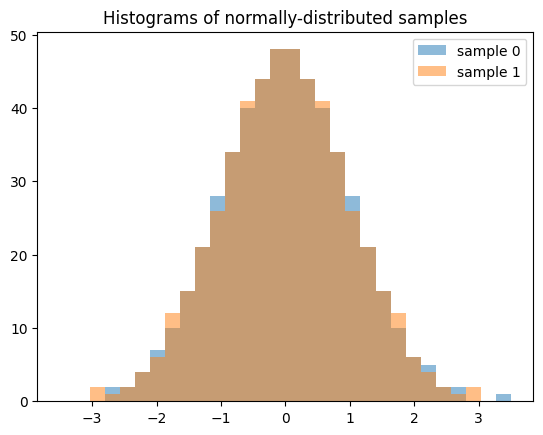
Обратите внимание, что при генерации нескольких выборок (например, len(shape) > 1), каждый срез вдоль нулевой оси является независимой последовательностью с низким расхождением. Следующее генерирует два независимых QMC-образца, каждый длиной 512.

samples = X.sample((512, 2), rng=qrng)
plt.hist(samples[:, 0], bins, alpha=0.5, label='sample 0')
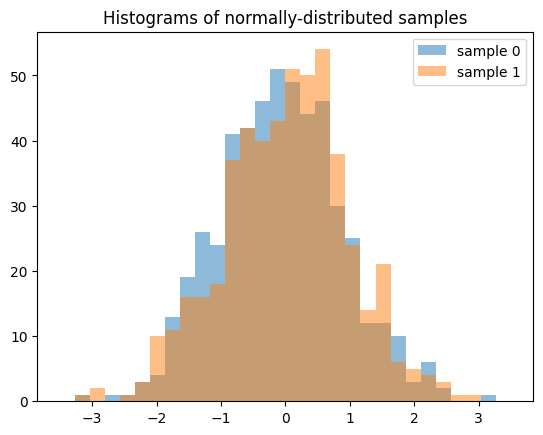
plt.hist(samples[:, 1], bins, alpha=0.5, label='sample 1')
plt.title('Histograms of normally-distributed samples')
plt.legend()
plt.show()

Результат сильно отличается, если мы генерируем 512 независимых последовательностей QMC, каждая длиной 2.

samples = X.sample((2, 512), rng=qrng)
plt.hist(samples[0], bins, alpha=0.5, label='sample 0')
plt.hist(samples[1], bins, alpha=0.5, label='sample 1')
plt.title('Histograms of normally-distributed samples')
plt.legend()
plt.show()

Точность

Для некоторых распределений, таких как scipy.stats.norm, почти все методы распределения адаптированы для обеспечения точных вычислений. Для других, таких как scipy.stats.gausshyper, определён лишь PDF, а остальные методы должны вычисляться численно на основе PDF. Например, функция выживания (дополнительная CDF) для гипергеометрического распределения Гаусса вычисляется численным интегрированием PDF от 0 find_repeats x для получения CDF, затем берётся дополнение.

a, b, c, z = 1.5, 2.5, 2, 0
x = 0.5
frozen = stats.gausshyper(a=a, b=b, c=c, z=z)
frozen.sf(x)

np.float64(0.28779340921080643)

frozen.sf(x) == 1 - integrate.quad(frozen.pdf, 0, x)[0]

np.True_

Однако другой подход — численно интегрировать PDF от x to 1 (правый конец носителя).

integrate.quad(frozen.pdf, x, 1)[0]

0.28779340919669805

Это различные, но одинаково валидные подходы, поэтому, предполагая точность PDF, маловероятно, что два результата неточны одинаковым образом. Следовательно, мы можем оценить точность результатов, сравнив их.

res1 = frozen.sf(x)
res2 = integrate.quad(frozen.pdf, x, 1)[0]
abs((res1 - res2) / res1)

np.float64(4.902259981810363e-11)

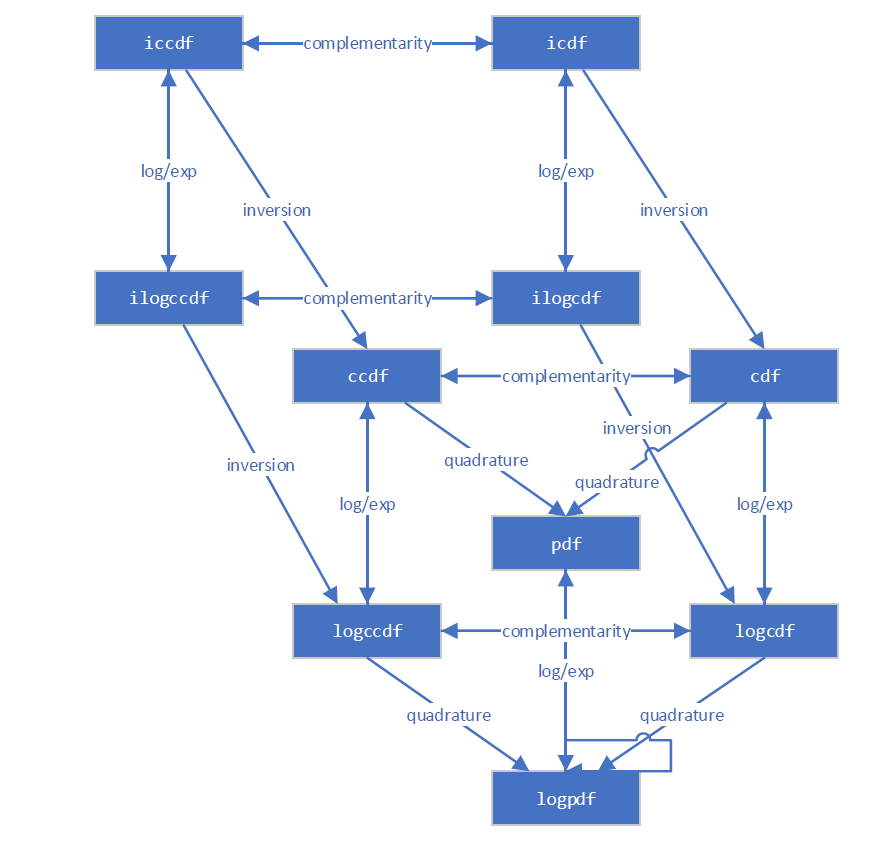
Новая инфраструктура учитывает несколько различных способов вычисления большинства величин. Например, эта диаграмма иллюстрирует взаимосвязи между различными функциями распределения.

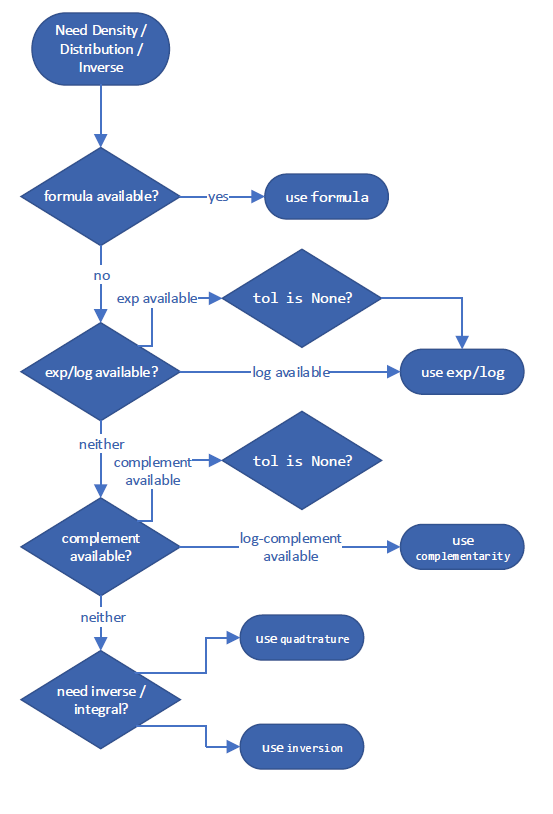
Он следует дереву решений, чтобы выбрать то, что, как ожидается, будет наиболее точным способом оценки величины. Эти конкретные деревья решений для «лучшего» метода могут меняться между версиями SciPy, но пример вычисления дополнительной CDF может выглядеть примерно так:

и для вычисления момента:

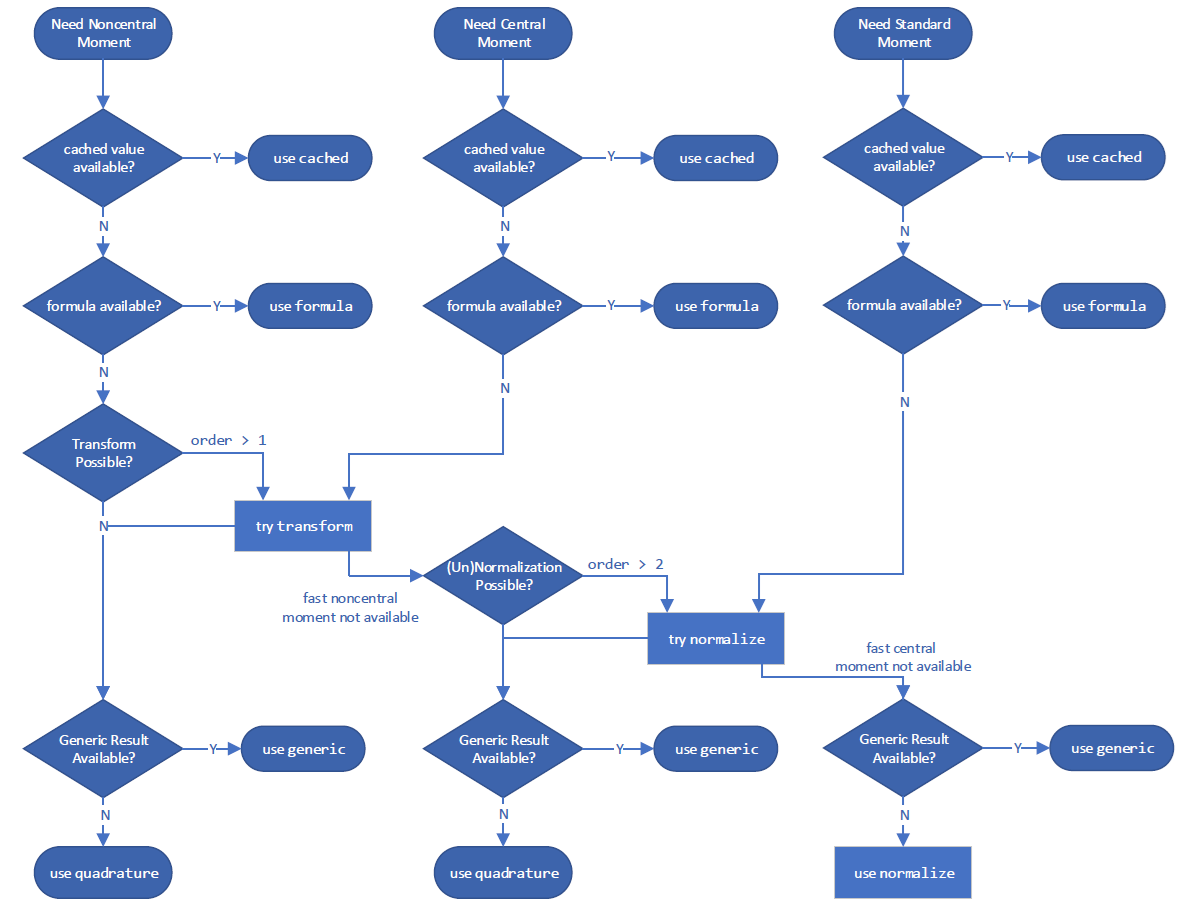
Однако вы можете переопределить используемый метод с помощью method аргумент.

GaussHyper = stats.make_distribution(stats.gausshyper)
X = GaussHyper(a=a, b=b, c=c, z=z)

Для ccdf, method='quadrature' интегрирует PDF в правом хвосте.

X.ccdf(x, method='quadrature') == integrate.tanhsinh(X.pdf, x, 1).integral

np.True_

method='complement' берёт дополнение CDF.

X.ccdf(x, method='complement') == (1 - integrate.tanhsinh(X.pdf, 0, x).integral)

np.True_

method='logexp' берёт экспоненту от логарифма CCDF.

X.ccdf(x, method='logexp') == np.exp(integrate.tanhsinh(lambda x: X.logpdf(x), x, 1, log=True).integral)

np.True_

Если сомневаетесь, попробуйте разные methods для вычисления заданной величины.

Производительность

Рассмотрим производительность вычислений, связанных с распределением Гаусса гипергеометрической функции. Для скалярных форм и аргументов производительность новой и старой инфраструктур сопоставима. Новая инфраструктура не ожидается значительно быстрее; хотя она уменьшает «накладные расходы» на проверку параметров, она не значительно быстрее при численном интегрировании скалярных величин, и последнее доминирует во времени выполнения здесь.

%timeit X.cdf(x)  # new infrastructure

393 μs ± 8.84 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

%timeit stats.gausshyper.cdf(x, a, b, c, z)  # old infrastructure

342 μs ± 682 ns per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

np.isclose(X.cdf(x), stats.gausshyper.cdf(x, a, b, c, z))

np.True_

Но новая инфраструктура намного быстрее при работе с массивами. Это связано с тем, что базовый интегратор (scipy.integrate.tanhsinh) и поиск корня (scipy.optimize.elementwise.find_root), разработанные для новой инфраструктуры, изначально векторизованы, тогда как устаревшие процедуры, используемые старой инфраструктурой (scipy.integrate.quad и scipy.optimize.brentq) не являются.

x = np.linspace(0, 1, 1000)

%timeit X.cdf(x)  # new infrastructure

2.38 ms ± 940 ns per loop (mean ± std. dev. of 7 runs, 100 loops each)

%timeit stats.gausshyper.cdf(x, a, b, c, z)  # old infrastructure

298 ms ± 188 μs per loop (mean ± std. dev. of 7 runs, 1 loop each)

Сопоставимое улучшение производительности можно ожидать для вычислений с массивами, когда базовые функции вычисляются либо численным интегрированием, либо инверсией (нахождением корней).

Визуализация

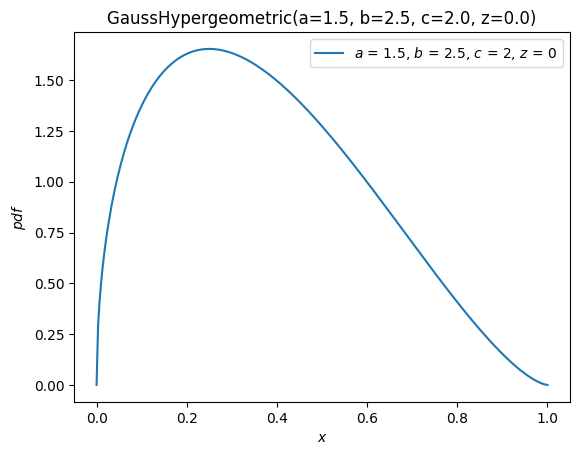
Мы можем легко визуализировать функции распределения, лежащие в основе случайных величин, используя удобный метод, plot.

import matplotlib.pyplot as plt
ax = X.plot()
plt.show()

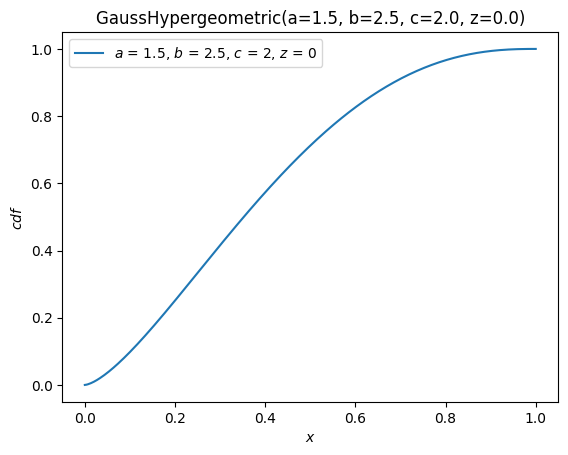
X.plot(y='cdf')
plt.show()

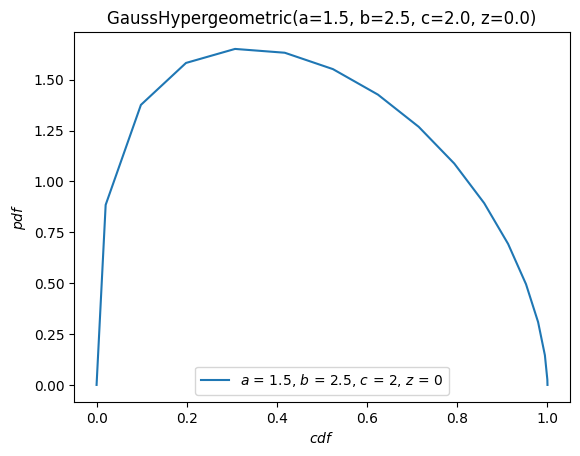
The plot метод достаточно гибкий, с сигнатурой, вдохновлённой Грамматика графики. Например, с аргументом \(x\) на \([-10, 10]\), построить PDF против CDF.

X.plot('cdf', 'pdf', t=('x', -10, 10))
plt.show()

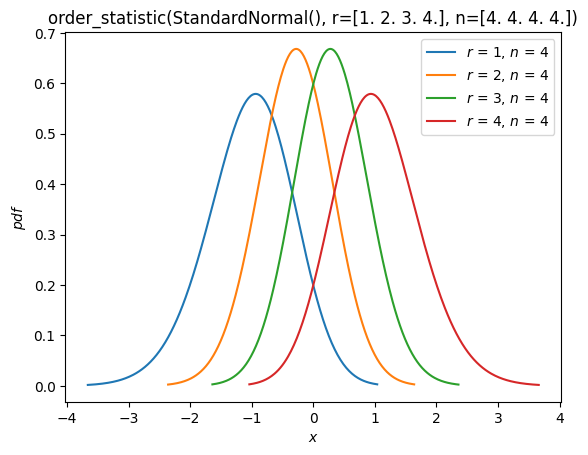
Порядковые статистики

Как видно в разделе "Fit" выше, теперь поддерживаются распределения порядковые статистики случайных выборок из распределения. Например, мы можем построить функции плотности вероятности порядковых статистик нормального распределения с размером выборки 4.

n = 4
r = np.arange(1, n+1)
X = stats.Normal()
Y = stats.order_statistic(X, r=r, n=n)
Y.plot()
plt.show()

Вычислить ожидаемые значения этих порядковых статистик:

Y.mean()

array([-1.02937537, -0.29701138,  0.29701138,  1.02937537])

Заключение

Хотя изменения могут быть неудобными, новая инфраструктура прокладывает путь к улучшенному опыту для пользователей вероятностных распределений SciPy. Это, конечно, не завершено! На момент написания этого руководства следующие функции запланированы для будущих выпусков:

• В частности, процедура строит сплайн-функцию Normal и Uniform)

• Дискретные распределения

• Круговые распределения, включая возможность оборачивания произвольных непрерывных распределений вокруг окружности

• Поддержка других бэкендов, совместимых с Python Array API, помимо NumPy (например, CuPy, PyTorch, JAX)

Как всегда, разработка SciPy ведётся для сообщества SciPy by сообщество SciPy. Предложения по другим функциям и помощь в их реализации всегда приветствуются.

Мы надеемся, что это руководство мотивирует преимущества использования новой инфраструктуры и упрощает процесс.