Пространственные структуры данных и алгоритмы (scipy.spatial)#
scipy.spatial может вычислять триангуляции, диаграммы Вороного и
выпуклые оболочки множества точек, используя Qhull библиотека.
Более того, он содержит KDTree реализации для запросов ближайших соседей и утилиты для вычисления расстояний в различных метриках.
Триангуляции Делоне#
Триангуляция Делоне - это разбиение множества точек на непересекающееся множество треугольников, такое, что ни одна точка не находится внутри описанной окружности любого треугольника. На практике такие триангуляции стремятся избегать треугольников с малыми углами.
Триангуляция Делоне может быть вычислена с использованием scipy.spatial следующим образом:
>>> from scipy.spatial import Delaunay
>>> import numpy as np
>>> points = np.array([[0, 0], [0, 1.1], [1, 0], [1, 1]])
>>> tri = Delaunay(points)
Мы можем визуализировать это:
>>> import matplotlib.pyplot as plt
>>> plt.triplot(points[:,0], points[:,1], tri.simplices)
>>> plt.plot(points[:,0], points[:,1], 'o')
И добавить некоторые дополнительные украшения:
>>> for j, p in enumerate(points):
... plt.text(p[0]-0.03, p[1]+0.03, j, ha='right') # label the points
>>> for j, s in enumerate(tri.simplices):
... p = points[s].mean(axis=0)
... plt.text(p[0], p[1], '#%d' % j, ha='center') # label triangles
>>> plt.xlim(-0.5, 1.5); plt.ylim(-0.5, 1.5)
>>> plt.show()
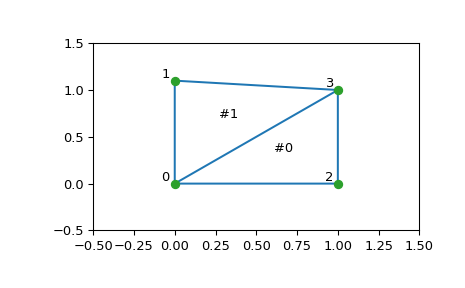
Структура триангуляции кодируется следующим образом:
simplices атрибут содержит индексы точек в
points массив, составляющий треугольник. Например:
>>> i = 1
>>> tri.simplices[i,:]
array([3, 1, 0], dtype=int32)
>>> points[tri.simplices[i,:]]
array([[ 1. , 1. ],
[ 0. , 1.1],
[ 0. , 0. ]])
Более того, соседние треугольники также могут быть найдены:
>>> tri.neighbors[i]
array([-1, 0, -1], dtype=int32)
Это говорит нам о том, что этот треугольник имеет треугольник #0 в качестве соседа, но не имеет других соседей. Более того, это говорит нам, что сосед 0 противоположен вершине 1 треугольника:
>>> points[tri.simplices[i, 1]]
array([ 0. , 1.1])
Действительно, из рисунка мы видим, что это так.
Qhull также может выполнять тесселяции до симплексов для многомерных наборов точек (например, разбиение на тетраэдры в 3-D).
Компланарные точки#
Важно отметить, что не все точки обязательно появляются как вершины триангуляции из-за проблем с численной точностью при формировании триангуляции. Рассмотрим вышеуказанное с дублированной точкой:
>>> points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
>>> tri = Delaunay(points)
>>> np.unique(tri.simplices.ravel())
array([0, 1, 2, 3], dtype=int32)
Обратите внимание, что точка #4, которая является дубликатом, не появляется как вершина триангуляции. То, что это произошло, записано:
>>> tri.coplanar
array([[4, 0, 3]], dtype=int32)
Это означает, что точка 4 находится рядом с треугольником 0 и вершиной 3, но не включена в триангуляцию.
Обратите внимание, что такие вырожденности могут возникать не только из-за дублированных точек, но и по более сложным геометрическим причинам, даже в наборах точек, которые на первый взгляд кажутся хорошо себя ведущими.
Однако Qhull имеет опцию «QJ», которая предписывает ему случайным образом возмущать входные данные до разрешения вырожденностей:
>>> tri = Delaunay(points, qhull_options="QJ Pp")
>>> points[tri.simplices]
array([[[1, 0],
[1, 1],
[0, 0]],
[[1, 1],
[1, 1],
[1, 0]],
[[1, 1],
[0, 1],
[0, 0]],
[[0, 1],
[1, 1],
[1, 1]]])
Появились два новых треугольника. Однако видно, что они вырождены и имеют нулевую площадь.
Выпуклые оболочки#
Выпуклая оболочка - это наименьший выпуклый объект, содержащий все точки в заданном наборе точек.
Они могут быть вычислены с помощью обёрток Qhull в scipy.spatial как
следует:
>>> from scipy.spatial import ConvexHull
>>> rng = np.random.default_rng()
>>> points = rng.random((30, 2)) # 30 random points in 2-D
>>> hull = ConvexHull(points)
Выпуклая оболочка представлена как набор N 1-D симплексов, что в 2-D означает отрезки. Схема хранения точно такая же, как для симплексов в триангуляции Делоне, обсуждавшейся выше.
Мы можем проиллюстрировать приведенный выше результат:
>>> import matplotlib.pyplot as plt
>>> plt.plot(points[:,0], points[:,1], 'o')
>>> for simplex in hull.simplices:
... plt.plot(points[simplex,0], points[simplex,1], 'k-')
>>> plt.show()
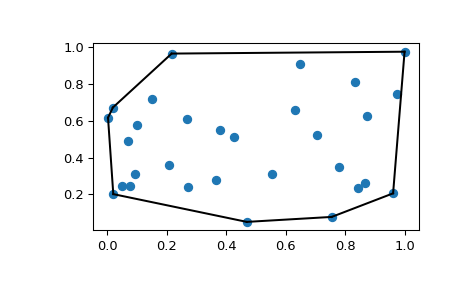
Того же можно достичь с помощью scipy.spatial.convex_hull_plot_2d.
Диаграммы Вороного#
Диаграмма Вороного — это разбиение пространства на ближайшие окрестности заданного набора точек.
Существует два способа обращения к этому объекту с помощью scipy.spatial.
Во-первых, можно использовать KDTree чтобы ответить на вопрос «какая из
точек ближе всего к этой», и определить области таким образом:
>>> from scipy.spatial import KDTree
>>> points = np.array([[0, 0], [0, 1], [0, 2], [1, 0], [1, 1], [1, 2],
... [2, 0], [2, 1], [2, 2]])
>>> tree = KDTree(points)
>>> tree.query([0.1, 0.1])
(0.14142135623730953, 0)
Таким образом, точка (0.1, 0.1) принадлежит региону 0. В цвете:
>>> x = np.linspace(-0.5, 2.5, 31)
>>> y = np.linspace(-0.5, 2.5, 33)
>>> xx, yy = np.meshgrid(x, y)
>>> xy = np.c_[xx.ravel(), yy.ravel()]
>>> import matplotlib.pyplot as plt
>>> dx_half, dy_half = np.diff(x[:2])[0] / 2., np.diff(y[:2])[0] / 2.
>>> x_edges = np.concatenate((x - dx_half, [x[-1] + dx_half]))
>>> y_edges = np.concatenate((y - dy_half, [y[-1] + dy_half]))
>>> plt.pcolormesh(x_edges, y_edges, tree.query(xy)[1].reshape(33, 31), shading='flat')
>>> plt.plot(points[:,0], points[:,1], 'ko')
>>> plt.show()
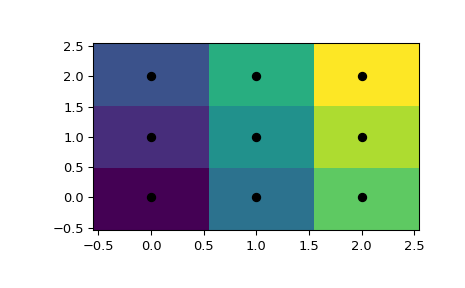
Это, однако, не даёт диаграмму Вороного как геометрический объект.
Представление в терминах линий и точек можно снова
получить через обёртки Qhull в scipy.spatial:
>>> from scipy.spatial import Voronoi
>>> vor = Voronoi(points)
>>> vor.vertices
array([[0.5, 0.5],
[0.5, 1.5],
[1.5, 0.5],
[1.5, 1.5]])
Вершины Вороного обозначают набор точек, формирующих полигональные границы регионов Вороного. В данном случае существует 9 различных регионов:
>>> vor.regions
[[], [-1, 0], [-1, 1], [1, -1, 0], [3, -1, 2], [-1, 3], [-1, 2], [0, 1, 3, 2], [2, -1, 0], [3, -1, 1]]
Отрицательное значение -1 снова указывает на точку в бесконечности. Действительно, только одна из областей, [0, 1, 3, 2], ограничен. Обратите внимание, что из-за проблем с численной точностью, аналогичных триангуляции Делоне выше, может быть меньше областей Вороного, чем входных точек.
Гребни (линии в 2-D), разделяющие регионы, описываются как аналогичная коллекция симплексов, как части выпуклой оболочки:
>>> vor.ridge_vertices
[[-1, 0], [-1, 0], [-1, 1], [-1, 1], [0, 1], [-1, 3], [-1, 2], [2, 3], [-1, 3], [-1, 2], [1, 3], [0, 2]]
Эти числа представляют индексы вершин Вороного, составляющих
отрезки линий. -1 снова является точкой в бесконечности — только 4 из
12 линий представляют собой ограниченный отрезок, в то время как остальные простираются до
бесконечности.
Гребни Вороного перпендикулярны линиям, проведённым между входными точками. Также записано, каким двум точкам соответствует каждый гребень:
>>> vor.ridge_points
array([[0, 3],
[0, 1],
[2, 5],
[2, 1],
[1, 4],
[7, 8],
[7, 6],
[7, 4],
[8, 5],
[6, 3],
[4, 5],
[4, 3]], dtype=int32)
Эта информация, взятая вместе, достаточна для построения полной диаграммы.
Мы можем построить это следующим образом. Сначала точки и вершины Вороного:
>>> plt.plot(points[:, 0], points[:, 1], 'o')
>>> plt.plot(vor.vertices[:, 0], vor.vertices[:, 1], '*')
>>> plt.xlim(-1, 3); plt.ylim(-1, 3)
Построение конечных отрезков линии происходит как для выпуклой оболочки, но теперь мы должны учитывать бесконечные ребра:
>>> for simplex in vor.ridge_vertices:
... simplex = np.asarray(simplex)
... if np.all(simplex >= 0):
... plt.plot(vor.vertices[simplex, 0], vor.vertices[simplex, 1], 'k-')
Гребни, простирающиеся до бесконечности, требуют немного больше внимания:
>>> center = points.mean(axis=0)
>>> for pointidx, simplex in zip(vor.ridge_points, vor.ridge_vertices):
... simplex = np.asarray(simplex)
... if np.any(simplex < 0):
... i = simplex[simplex >= 0][0] # finite end Voronoi vertex
... t = points[pointidx[1]] - points[pointidx[0]] # tangent
... t = t / np.linalg.norm(t)
... n = np.array([-t[1], t[0]]) # normal
... midpoint = points[pointidx].mean(axis=0)
... far_point = vor.vertices[i] + np.sign(np.dot(midpoint - center, n)) * n * 100
... plt.plot([vor.vertices[i,0], far_point[0]],
... [vor.vertices[i,1], far_point[1]], 'k--')
>>> plt.show()
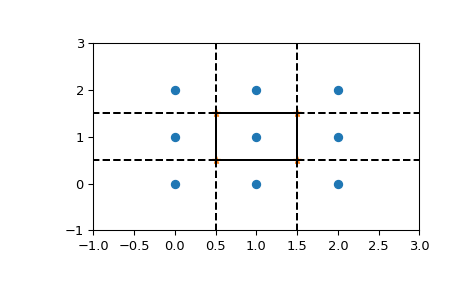
Этот график также можно создать с помощью scipy.spatial.voronoi_plot_2d.
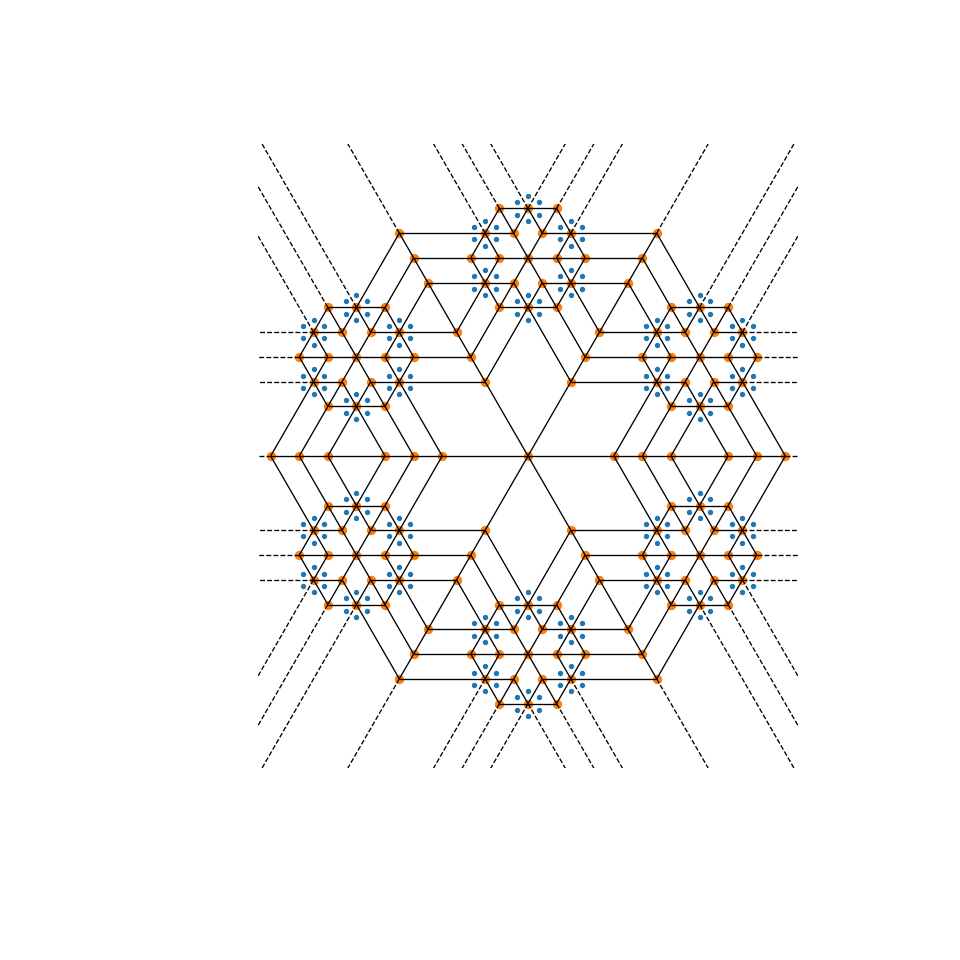
Диаграммы Вороного можно использовать для создания интересного генеративного искусства. Попробуйте поиграть с настройками этого mandala функцию для создания своей собственной!
>>> import numpy as np
>>> from scipy import spatial
>>> import matplotlib.pyplot as plt
>>> def mandala(n_iter, n_points, radius):
... """Creates a mandala figure using Voronoi tessellations.
...
... Parameters
... ----------
... n_iter : int
... Number of iterations, i.e. how many times the equidistant points will
... be generated.
... n_points : int
... Number of points to draw per iteration.
... radius : scalar
... The radial expansion factor.
...
... Returns
... -------
... fig : matplotlib.Figure instance
...
... Notes
... -----
... This code is adapted from the work of Audrey Roy Greenfeld [1]_ and Carlos
... Focil-Espinosa [2]_, who created beautiful mandalas with Python code. That
... code in turn was based on Antonio Sánchez Chinchón's R code [3]_.
...
... References
... ----------
... .. [1] https://www.codemakesmehappy.com/2019/09/voronoi-mandalas.html
...
... .. [2] https://github.com/CarlosFocil/mandalapy
...
... .. [3] https://github.com/aschinchon/mandalas
...
... """
... fig = plt.figure(figsize=(10, 10))
... ax = fig.add_subplot(111)
... ax.set_axis_off()
... ax.set_aspect('equal', adjustable='box')
...
... angles = np.linspace(0, 2*np.pi * (1 - 1/n_points), num=n_points) + np.pi/2
... # Starting from a single center point, add points iteratively
... xy = np.array([[0, 0]])
... for k in range(n_iter):
... t1 = np.array([])
... t2 = np.array([])
... # Add `n_points` new points around each existing point in this iteration
... for i in range(xy.shape[0]):
... t1 = np.append(t1, xy[i, 0] + radius**k * np.cos(angles))
... t2 = np.append(t2, xy[i, 1] + radius**k * np.sin(angles))
...
... xy = np.column_stack((t1, t2))
...
... # Create the Mandala figure via a Voronoi plot
... spatial.voronoi_plot_2d(spatial.Voronoi(xy), ax=ax)
...
... return fig
>>> # Modify the following parameters in order to get different figures
>>> n_iter = 3
>>> n_points = 6
>>> radius = 4
>>> fig = mandala(n_iter, n_points, radius)
>>> plt.show()