Специальные функции (scipy.special)

Основная особенность scipy.special пакет содержит определения многочисленных специальных функций математической физики. Доступные функции включают эйри, эллиптические, бесселевы, гамма, бета, гипергеометрические, параболического цилиндра, Матье, сфероидальных волн, Струве и Кельвина. Также имеются некоторые низкоуровневые статистические функции, которые не предназначены для общего использования, поскольку более удобный интерфейс к этим функциям предоставляется stats модуля. Большинство этих функций могут принимать аргументы массива и возвращать результаты массива, следуя тем же правилам широковещания, что и другие математические функции в Numerical Python. Многие из этих функций также принимают комплексные числа в качестве входных данных. Для полного списка доступных функций с однострочным описанием введите >>> help(special). Каждая функция также имеет свою собственную документацию, доступную с помощью help. Если вы не видите нужную функцию, рассмотрите возможность её написания и внесения в библиотеку. Вы можете написать функцию на C, Fortran или Python. Посмотрите в исходном коде библиотеки примеры каждого из этих типов функций.

Функции Бесселя вещественного порядка(jv, jn_zeros)

Функции Бесселя — это семейство решений дифференциального уравнения Бесселя с действительным или комплексным порядком alpha:

\[x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0\]

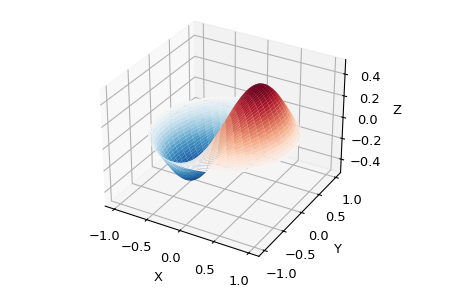
Среди прочих применений, эти функции возникают в задачах распространения волн, таких как вибрационные моды тонкой мембраны барабана. Вот пример круглой мембраны барабана, закреплённой по краю:

>>> from scipy import special
>>> import numpy as np
>>> def drumhead_height(n, k, distance, angle, t):
...    kth_zero = special.jn_zeros(n, k)[-1]
...    return np.cos(t) * np.cos(n*angle) * special.jn(n, distance*kth_zero)
>>> theta = np.r_[0:2*np.pi:50j]
>>> radius = np.r_[0:1:50j]
>>> x = np.array([r * np.cos(theta) for r in radius])
>>> y = np.array([r * np.sin(theta) for r in radius])
>>> z = np.array([drumhead_height(1, 1, r, theta, 0.5) for r in radius])

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_axes(rect=(0, 0.05, 0.95, 0.95), projection='3d')
>>> ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='RdBu_r', vmin=-0.5, vmax=0.5)
>>> ax.set_xlabel('X')
>>> ax.set_ylabel('Y')
>>> ax.set_xticks(np.arange(-1, 1.1, 0.5))
>>> ax.set_yticks(np.arange(-1, 1.1, 0.5))
>>> ax.set_zlabel('Z')
>>> plt.show()

Привязки Cython для специальных функций (scipy.special.cython_special)

SciPy также предлагает привязки Cython для скалярных типизированных версий многих функций в special. Следующий код Cython дает простой пример использования этих функций:

cimport scipy.special.cython_special as csc

cdef:
    double x = 1
    double complex z = 1 + 1j
    double si, ci, rgam
    double complex cgam

rgam = csc.gamma(x)
print(rgam)
cgam = csc.gamma(z)
print(cgam)
csc.sici(x, &si, &ci)
print(si, ci)

(См. Документация Cython для помощи в компиляции Cython.) В примере функция csc.gamma работает по сути как его аналог ufunc gamma, хотя она принимает аргументы типов C вместо массивов NumPy. Обратите внимание, в частности, что функция перегружена для поддержки вещественных и комплексных аргументов; правильный вариант выбирается во время компиляции. Функция csc.sici работает немного иначе, чем sici; для ufunc мы могли бы написать ai, bi = sici(x), тогда как в версии на Cython несколько возвращаемых значений передаются как указатели. Может помочь думать об этом как о вызове ufunc с выходным массивом: sici(x, out=(si, ci)).

Есть два потенциальных преимущества использования привязок Cython:

• они избегают накладных расходов на вызовы функций Python

• они не требуют глобальной блокировки интерпретатора Python (GIL)

В следующих разделах обсуждается, как использовать эти преимущества для потенциального ускорения вашего кода, хотя, конечно, всегда следует сначала профилировать код, чтобы убедиться, что дополнительные усилия будут стоить того.

Избегание накладных расходов Python-функций

Для ufuncs в special, накладные расходы на вызов Python-функции избегаются путем векторизации, то есть передачи массива в функцию. Обычно этот подход работает довольно хорошо, но иногда удобнее вызывать специальную функцию на скалярных входах внутри цикла, например, при реализации собственного ufunc. В этом случае накладные расходы на вызов Python-функции могут стать значительными. Рассмотрим следующий пример:

import scipy.special as sc
cimport scipy.special.cython_special as csc

def python_tight_loop():
    cdef:
        int n
        double x = 1

    for n in range(100):
        sc.jv(n, x)

def cython_tight_loop():
    cdef:
        int n
        double x = 1

    for n in range(100):
        csc.jv(n, x)

На одном компьютере python_tight_loop заняло около 131 микросекунды для выполнения и cython_tight_loop заняло около 18.2 микросекунд для выполнения. Очевидно, этот пример искусственный: можно было бы просто вызвать special.jv(np.arange(100), 1) и получать результаты так же быстро, как в cython_tight_loopСуть в том, что если накладные расходы на вызов функций Python становятся значительными в вашем коде, то привязки Cython могут быть полезны.

Освобождение GIL

Часто требуется вычислять специальную функцию во многих точках, и обычно вычисления тривиально распараллеливаются. Поскольку привязки Cython не требуют GIL, легко запускать их параллельно, используя prange функция. Например, предположим, что мы хотим вычислить фундаментальное решение уравнения Гельмгольца:

\[\Delta_x G(x, y) + k^2G(x, y) = \delta(x - y),\]

где \(k\) является волновым числом и \(\delta\) это дельта-функция Дирака. Известно, что в двух измерениях единственное (излучающее) решение

\[G(x, y) = \frac{i}{4}H_0^{(1)}(k|x - y|),\]

где \(H_0^{(1)}\) является функцией Ханкеля первого рода, т.е. функцией hankel1. Следующий пример показывает, как мы могли бы вычислять эту функцию параллельно:

from libc.math cimport fabs
cimport cython
from cython.parallel cimport prange

import numpy as np
import scipy.special as sc
cimport scipy.special.cython_special as csc

def serial_G(k, x, y):
    return 0.25j*sc.hankel1(0, k*np.abs(x - y))

@cython.boundscheck(False)
@cython.wraparound(False)
cdef void _parallel_G(double k, double[:,:] x, double[:,:] y,
                      double complex[:,:] out) nogil:
    cdef int i, j

    for i in prange(x.shape[0]):
        for j in range(y.shape[0]):
            out[i,j] = 0.25j*csc.hankel1(0, k*fabs(x[i,j] - y[i,j]))

def parallel_G(k, x, y):
    out = np.empty_like(x, dtype='complex128')
    _parallel_G(k, x, y, out)
    return out

(Для помощи с компиляцией параллельного кода в Cython см. здесь.) Если приведенный выше код Cython находится в файле test.pyx, тогда мы можем написать неформальный бенчмарк, который сравнивает параллельную и последовательную версии функции:

import timeit

import numpy as np

from test import serial_G, parallel_G

def main():
    k = 1
    x, y = np.linspace(-100, 100, 1000), np.linspace(-100, 100, 1000)
    x, y = np.meshgrid(x, y)

    def serial():
        serial_G(k, x, y)

    def parallel():
        parallel_G(k, x, y)

    time_serial = timeit.timeit(serial, number=3)
    time_parallel = timeit.timeit(parallel, number=3)
    print("Serial method took {:.3} seconds".format(time_serial))
    print("Parallel method took {:.3} seconds".format(time_parallel))

if __name__ == "__main__":
    main()

На одноядерном компьютере последовательный метод занял 1.29 секунд, а параллельный метод занял 0.29 секунд.

Функции не в scipy.special

Некоторые функции не включены в special, потому что их легко реализовать с помощью существующих функций в NumPy и SciPy. Чтобы избежать изобретения велосипеда, этот раздел предоставляет реализации нескольких таких функций, которые, надеюсь, иллюстрируют, как обрабатывать похожие функции. Во всех примерах NumPy импортируется как np и special импортируется как sc.

The бинарная энтропийная функция:

def binary_entropy(x):
    return -(sc.xlogy(x, x) + sc.xlog1py(1 - x, -x))/np.log(2)

Прямоугольная ступенчатая функция на [0, 1]:

def step(x):
    return 0.5*(np.sign(x) + np.sign(1 - x))

Перемещение и масштабирование могут использоваться для получения произвольной ступенчатой функции.

The функция скачка:

def ramp(x):
    return np.maximum(0, x)