Многомерная обработка изображений (scipy.ndimage)#

Введение#

Обработка и анализ изображений обычно рассматриваются как операции над двумерными массивами значений. Однако существует ряд областей, где необходимо анализировать изображения более высокой размерности. Хорошими примерами являются медицинская визуализация и биологическая визуализация. numpy очень хорошо подходит для этого типа приложений благодаря своей врождённой многомерной природе. Этот scipy.ndimage пакеты предоставляют ряд общих функций обработки и анализа изображений, которые предназначены для работы с массивами произвольной размерности. Пакеты в настоящее время включают: функции для линейной и нелинейной фильтрации, бинарной морфологии, B-сплайновой интерполяции и измерений объектов.

Свойства, общие для всех функций#

Все функции имеют некоторые общие свойства. В частности, все функции позволяют указать выходной массив с помощью вывод аргумент. С этим аргументом можно указать массив, который будет изменен на месте результатом операции. В этом случае результат не возвращается. Обычно использование вывод аргумент является более эффективным, поскольку существующий массив используется для хранения результата.

Тип возвращаемых массивов зависит от типа операции, но в большинстве случаев он равен типу входных данных. Однако, если вывод аргумент используется, тип результата равен типу указанного выходного аргумента. Если выходной аргумент не задан, всё равно можно указать, каким должен быть результат вывода. Это делается простым присвоением желаемого numpy тип объекта к выходному аргументу. Например:

>>> from scipy.ndimage import correlate
>>> import numpy as np
>>> correlate(np.arange(10), [1, 2.5])
array([ 0,  2,  6,  9, 13, 16, 20, 23, 27, 30])
>>> correlate(np.arange(10), [1, 2.5], output=np.float64)
array([  0. ,   2.5,   6. ,   9.5,  13. ,  16.5,  20. ,  23.5,  27. ,  30.5])

Функции фильтрации#

Функции, описанные в этом разделе, выполняют некоторый тип пространственной фильтрации входного массива: элементы в выходных данных являются некоторой функцией значений в окрестности соответствующего входного элемента. Мы называем эту окрестность элементов ядром фильтра, которое часто имеет прямоугольную форму, но также может иметь произвольный след. Многие из описанных ниже функций позволяют определить след ядра, передавая маску через footprint параметр. Например, крестообразное ядро может быть определено следующим образом:

>>> footprint = np.array([[0, 1, 0], [1, 1, 1], [0, 1, 0]])
>>> footprint
array([[0, 1, 0],
       [1, 1, 1],
       [0, 1, 0]])

Обычно начало ядра находится в центре, вычисленном делением размеров формы ядра на два. Например, начало 1-D ядра длиной три находится на втором элементе. Возьмем, к примеру, корреляцию 1-D массива с фильтром длиной 3, состоящим из единиц:

>>> from scipy.ndimage import correlate1d
>>> a = [0, 0, 0, 1, 0, 0, 0]
>>> correlate1d(a, [1, 1, 1])
array([0, 0, 1, 1, 1, 0, 0])

Иногда удобно выбрать другое начало для ядра. По этой причине большинство функций поддерживают origin параметр, который задает начало фильтра относительно его центра. Например:

>>> a = [0, 0, 0, 1, 0, 0, 0]
>>> correlate1d(a, [1, 1, 1], origin = -1)
array([0, 1, 1, 1, 0, 0, 0])

Эффект представляет собой сдвиг результата влево. Эта функция не будет часто нужна, но может быть полезна, особенно для фильтров с чётным размером. Хороший пример — вычисление обратных и прямых разностей:

>>> a = [0, 0, 1, 1, 1, 0, 0]
>>> correlate1d(a, [-1, 1])               # backward difference
array([ 0,  0,  1,  0,  0, -1,  0])
>>> correlate1d(a, [-1, 1], origin = -1)  # forward difference
array([ 0,  1,  0,  0, -1,  0,  0])

Мы также могли бы вычислить прямую разность следующим образом:

>>> correlate1d(a, [0, -1, 1])
array([ 0,  1,  0,  0, -1,  0,  0])

Однако использование параметра origin вместо большего ядра более эффективно. Для многомерных ядер, origin может быть числом, в этом случае начало координат предполагается одинаковым по всем осям, или последовательностью, задающей начало по каждой оси.

Поскольку выходные элементы являются функцией элементов в окрестности входных элементов, границы массива должны быть обработаны соответствующим образом путем предоставления значений за пределами границ. Это делается путем предположения, что массивы расширены за свои границы в соответствии с определенными граничными условиями. В функциях, описанных ниже, граничные условия могут быть выбраны с использованием mode параметр, который должен быть строкой с именем граничного условия. В настоящее время поддерживаются следующие граничные условия:

mode

описание

пример

“ближайший”

использовать значение на границе

[1 2 3]->[1 1 2 3 3]

“wrap”

периодически реплицировать массив

[1 2 3]->[3 1 2 3 1]

“отражать”

отразить массив на границе

[1 2 3]->[1 1 2 3 3]

“зеркальный”

отразить массив на границе

[1 2 3]->[2 1 2 3 2]

"constant"

использовать постоянное значение, по умолчанию 0.0

[1 2 3]->[0 1 2 3 0]

Для совместимости с процедурами интерполяции также поддерживаются следующие синонимы:

mode

описание

“grid-constant”

эквивалентно «constant»*

“grid-mirror”

эквивалентно "reflect"

“grid-wrap”

эквивалентно "wrap"

* “grid-constant” и “constant” эквивалентны для операций фильтрации, но имеют разное поведение в функциях интерполяции. Для согласованности API функции фильтрации принимают любое из этих имен.

Режим 'constant' особенный, так как требует дополнительный параметр для указания постоянного значения, которое должно использоваться.

Обратите внимание, что режимы mirror и reflect отличаются только тем, повторяется ли образец на границе при отражении. Для режима mirror точка симметрии находится точно на последнем образце, поэтому это значение не повторяется. Этот режим также известен как whole-sample symmetric, поскольку точка симметрии попадает на последний образец. Аналогично, reflect часто называют half-sample symmetric, так как точка симметрии находится на полобразца за границей массива.

Примечание

Самый простой способ реализации таких граничных условий — это копирование данных в больший массив и расширение данных на границах в соответствии с граничными условиями. Для больших массивов и больших фильтрующих ядер это потребовало бы много памяти, поэтому функции, описанные ниже, используют другой подход, не требующий выделения больших временных буферов.

Корреляция и свёртка#

  • The correlate1d функция вычисляет 1-D корреляцию вдоль заданной оси. Строки массива вдоль заданной оси коррелируют с заданным веса. веса параметр должен быть одномерной последовательностью чисел.

  • Функция correlate реализует многомерную корреляцию входного массива с заданным ядром.

  • The convolve1d функция вычисляет одномерную свёртку вдоль заданной оси. Строки массива вдоль заданной оси свёртываются с заданным веса. веса параметр должен быть одномерной последовательностью чисел.

  • Функция convolve реализует многомерную свёртку входного массива с заданным ядром.

    Примечание

    Свёртка по сути является корреляцией после отражения ядра. В результате, origin параметр ведет себя иначе, чем в случае корреляции: результат смещается в противоположном направлении.

Сглаживающие фильтры#

  • The gaussian_filter1d функция реализует одномерный фильтр Гаусса. Стандартное отклонение фильтра Гаусса передается через параметр sigma. Установка порядок = 0 соответствует свёртке с ядром Гаусса. Порядок 1, 2, или 3 соответствует свёртке с первой, второй или третьей производной Гаусса. Производные более высокого порядка не реализованы.

  • The gaussian_filter функция реализует многомерный фильтр Гаусса. Стандартные отклонения фильтра Гаусса по каждой оси передаются через параметр sigma как последовательность или числа. Если sigma не является последовательностью, а представляет собой одно число, стандартное отклонение фильтра одинаково по всем направлениям. Порядок фильтра может быть указан отдельно для каждой оси. Порядок 0 соответствует свертке с гауссовым ядром. Порядок 1, 2 или 3 соответствует свертке с первой, второй или третьей производной гауссовой функции. Производные более высокого порядка не реализованы. порядок параметр должен быть числом, чтобы указать тот же порядок для всех осей, или последовательностью чисел, чтобы указать разный порядок для каждой оси. Пример ниже показывает фильтр, примененный к тестовым данным с разными значениями sigma. порядок параметр остается равным 0.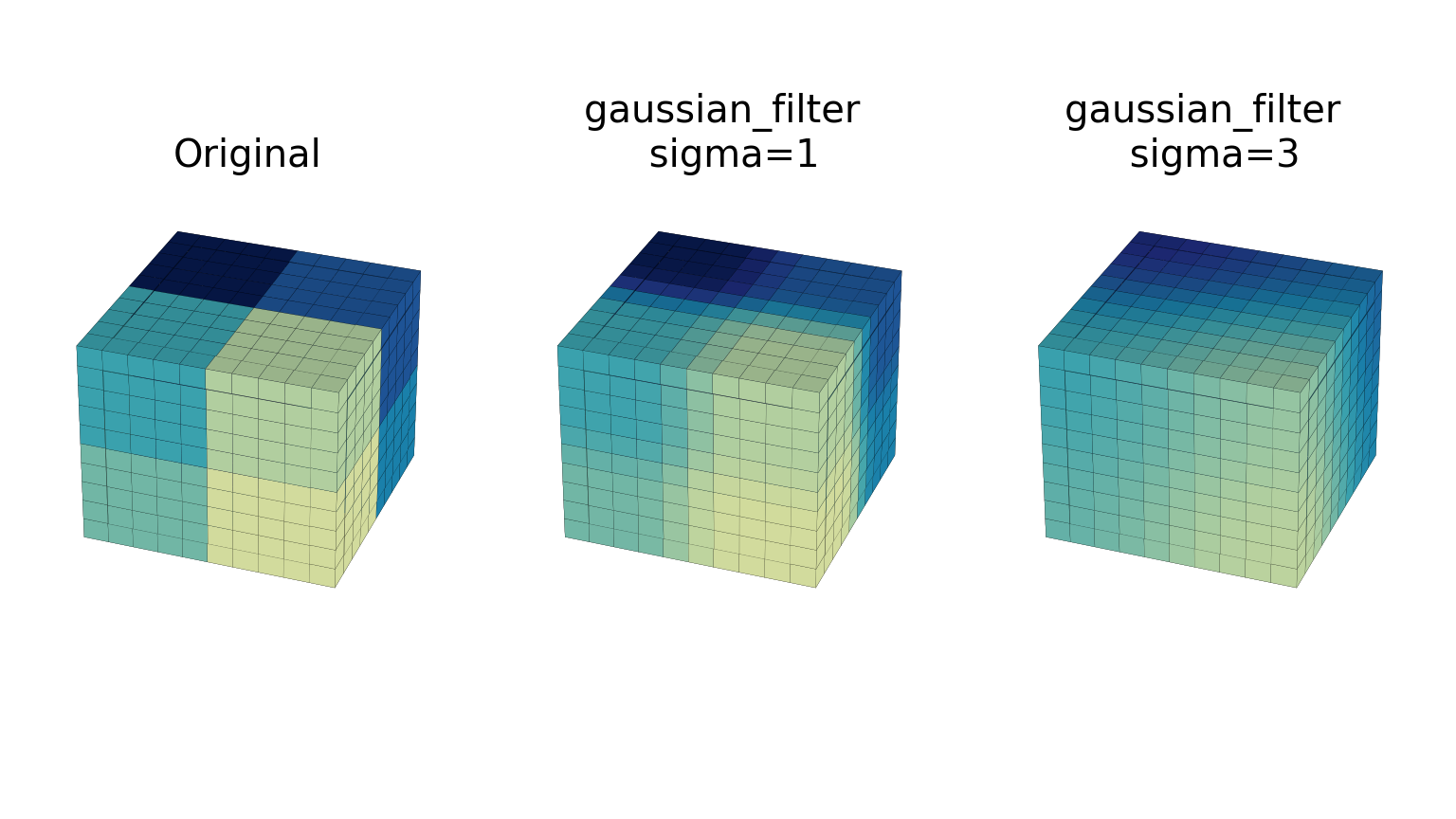

    " "

    Примечание

    Многомерный фильтр реализован как последовательность одномерных гауссовских фильтров. Промежуточные массивы хранятся в том же типе данных, что и выходные. Поэтому для выходных типов с меньшей точностью результаты могут быть неточными, поскольку промежуточные результаты могут храниться с недостаточной точностью. Этого можно избежать, указав более точный выходной тип.

  • The uniform_filter1d функция вычисляет одномерный равномерный фильтр для заданного размер вдоль заданной оси.

  • The uniform_filter реализует многомерный равномерный фильтр. Размеры равномерного фильтра задаются для каждой оси как последовательность целых чисел параметром размер параметр. Если размер не является последовательностью, а одиночным числом, размеры вдоль всех осей предполагаются равными.

    Примечание

    Многомерный фильтр реализован как последовательность одномерных равномерных фильтров. Промежуточные массивы хранятся в том же типе данных, что и выходные. Поэтому для выходных типов с меньшей точностью результаты могут быть неточными, поскольку промежуточные результаты могут храниться с недостаточной точностью. Этого можно избежать, указав более точный выходной тип.

Фильтры на основе порядковых статистик#

  • The minimum_filter1d функция вычисляет 1-D минимальный фильтр заданного размер вдоль заданной оси.

  • The maximum_filter1d функция вычисляет 1-D максимальный фильтр заданного размер вдоль заданной оси.

  • The minimum_filter функция вычисляет многомерный минимальный фильтр. Должны быть указаны либо размеры прямоугольного ядра, либо отпечаток ядра. размер параметр, если предоставлен, должен быть последовательностью размеров или одним числом, в этом случае размер фильтра предполагается равным вдоль каждой оси. Параметр footprint, если предоставлен, должен быть массивом, который определяет форму ядра своими ненулевыми элементами.

  • The maximum_filter функция вычисляет многомерный максимальный фильтр. Должны быть указаны либо размеры прямоугольного ядра, либо след ядра. размер параметр, если предоставлен, должен быть последовательностью размеров или одним числом, в этом случае размер фильтра предполагается равным вдоль каждой оси. Параметр footprint, если предоставлен, должен быть массивом, который определяет форму ядра своими ненулевыми элементами.

  • The rank_filter функция вычисляет многомерный ранговый фильтр. Эта rank может быть меньше нуля, т.е., rank = -1 указывает на наибольший элемент. Должны быть указаны либо размеры прямоугольного ядра, либо след ядра. размер параметр, если предоставлен, должен быть последовательностью размеров или одним числом, в этом случае размер фильтра предполагается равным по каждой оси. Параметр footprint, если предоставлено, должно быть массивом, который определяет форму ядра своими ненулевыми элементами.

  • The percentile_filter функция вычисляет многомерный процентильный фильтр. процентиль может быть меньше нуля, т.е., процентиль = -20 равно процентиль = 80. Либо размеры прямоугольного ядра, либо след ядра должны быть указаны. размер параметр, если указан, должен быть последовательностью размеров или одним числом, в этом случае размер фильтра считается одинаковым по каждой оси. footprint, если предоставлен, должен быть массивом, который определяет форму ядра своими ненулевыми элементами.

  • The median_filter функция вычисляет многомерный медианный фильтр. Должны быть указаны либо размеры прямоугольного ядра, либо след ядра. размер параметр, если предоставлен, должен быть последовательностью размеров или одним числом, в этом случае размер фильтра предполагается равным вдоль каждой оси. The footprint если предоставлен, должен быть массивом, который определяет форму ядра своими ненулевыми элементами.

Производные#

Производные фильтры могут быть построены несколькими способами. Функция gaussian_filter1d, описанные в Сглаживающие фильтры, можно использовать для вычисления производных вдоль заданной оси с помощью порядок параметр. Другие фильтры производных — это фильтры Превитта и Собеля:

  • The prewitt функция вычисляет производную вдоль заданной оси.

  • The sobel функция вычисляет производную вдоль заданной оси.

Фильтр Лапласа вычисляется суммой вторых производных по всем осям. Таким образом, различные фильтры Лапласа могут быть построены с использованием различных функций второй производной. Поэтому мы предоставляем общую функцию, которая принимает аргумент-функцию для вычисления второй производной вдоль заданного направления.

  • Функция generic_laplace вычисляет фильтр Лапласа с использованием функции, переданной через derivative2 для вычисления вторых производных. Функция derivative2 должен иметь следующую сигнатуру

    derivative2(input, axis, output, mode, cval, *extra_arguments, **extra_keywords)

    Он должен вычислять вторую производную по измерению ось. Если вывод не является None, он должен использовать это для вывода и возвращать None, в противном случае он должен возвращать результат. mode, cval имеют обычное значение.

    The extra_arguments и extra_keywords аргументы могут использоваться для передачи кортежа дополнительных аргументов и словаря именованных аргументов, которые передаются в derivative2 при каждом вызове.

    Например

    >>> def d2(input, axis, output, mode, cval):
...     return correlate1d(input, [1, -2, 1], axis, output, mode, cval, 0)
...
>>> a = np.zeros((5, 5))
>>> a[2, 2] = 1
>>> from scipy.ndimage import generic_laplace
>>> generic_laplace(a, d2)
array([[ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  1., -4.,  1.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.]])

    Для демонстрации использования extra_arguments аргумент, мы могли бы сделать

    >>> def d2(input, axis, output, mode, cval, weights):
...     return correlate1d(input, weights, axis, output, mode, cval, 0,)
...
>>> a = np.zeros((5, 5))
>>> a[2, 2] = 1
>>> generic_laplace(a, d2, extra_arguments = ([1, -2, 1],))
array([[ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  1., -4.,  1.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.]])

    или

    >>> generic_laplace(a, d2, extra_keywords = {'weights': [1, -2, 1]})
array([[ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  1., -4.,  1.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.]])

Следующие две функции реализованы с использованием generic_laplace предоставляя соответствующие функции для функции второй производной:

  • Функция laplace вычисляет Лапласа с использованием дискретного дифференцирования для второй производной (т.е., свертки с [1, -2, 1]).

  • Функция gaussian_laplace вычисляет фильтр Лапласа с использованием gaussian_filter для вычисления вторых производных. Стандартные отклонения гауссовского фильтра вдоль каждой оси передаются через параметр sigma как последовательность или числа. Если sigma не является последовательностью, а одиночным числом, стандартное отклонение фильтра одинаково по всем направлениям.

Величина градиента определяется как квадратный корень из суммы квадратов градиентов по всем направлениям. Подобно общей функции Лапласа, существует generic_gradient_magnitude функция, вычисляющая величину градиента массива.

  • Функция generic_gradient_magnitude вычисляет величину градиента с использованием функции, переданной через derivative для вычисления первых производных. Функция derivative должен иметь следующую сигнатуру

    derivative(input, axis, output, mode, cval, *extra_arguments, **extra_keywords)

    Он должен вычислять производную по размерности ось. Если вывод не является None, он должен использовать это для вывода и возвращать None, в противном случае должен возвращать результат. mode, cval имеют обычное значение.

    The extra_arguments и extra_keywords аргументы могут использоваться для передачи кортежа дополнительных аргументов и словаря именованных аргументов, которые передаются в производная при каждом вызове.

    Например, sobel функция соответствует требуемой сигнатуре

    >>> a = np.zeros((5, 5))
>>> a[2, 2] = 1
>>> from scipy.ndimage import sobel, generic_gradient_magnitude
>>> generic_gradient_magnitude(a, sobel)
array([[ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  1.41421356,  2.        ,  1.41421356,  0.        ],
       [ 0.        ,  2.        ,  0.        ,  2.        ,  0.        ],
       [ 0.        ,  1.41421356,  2.        ,  1.41421356,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ]])

    См. документацию generic_laplace для примеров использования extra_arguments и extra_keywords аргументы.

The sobel и prewitt функции соответствуют требуемой сигнатуре и, следовательно, могут использоваться напрямую с generic_gradient_magnitude.

  • Функция gaussian_gradient_magnitude вычисляет величину градиента с использованием gaussian_filter для вычисления первых производных. Стандартные отклонения гауссовского фильтра по каждой оси передаются через параметр sigma как последовательность или числа. Если sigma не является последовательностью, а одним числом, стандартное отклонение фильтра одинаково по всем направлениям.

Универсальные функции фильтрации#

Для реализации функций фильтрации можно использовать общие функции, которые принимают вызываемый объект, реализующий операцию фильтрации. Итерация по входным и выходным массивам обрабатывается этими общими функциями, включая такие детали, как реализация граничных условий. Необходимо предоставить только вызываемый объект, реализующий callback-функцию, которая выполняет фактическую работу фильтрации. Callback-функция также может быть написана на C и передана с использованием PyCapsule (см. Расширение scipy.ndimage на C для получения дополнительной информации).

  • The generic_filter1d функция реализует общую одномерную функцию фильтрации, где фактическая операция фильтрации должна быть предоставлена как функция Python (или другой вызываемый объект). generic_filter1d функция итерирует по строкам массива и вызывает function в каждой строке. Аргументы, передаваемые в function являются одномерными массивами numpy.float64 тип. Первый содержит значения текущей строки. Он расширяется в начале и конце, в соответствии с filter_size и origin аргументы. Второй массив должен быть изменён на месте, чтобы предоставить выходные значения линии. Например, рассмотрим корреляцию вдоль одного измерения:

    >>> a = np.arange(12).reshape(3,4)
>>> correlate1d(a, [1, 2, 3])
array([[ 3,  8, 14, 17],
       [27, 32, 38, 41],
       [51, 56, 62, 65]])

    Та же операция может быть реализована с использованием generic_filter1d, следующим образом:

    >>> def fnc(iline, oline):
...     oline[...] = iline[:-2] + 2 * iline[1:-1] + 3 * iline[2:]
...
>>> from scipy.ndimage import generic_filter1d
>>> generic_filter1d(a, fnc, 3)
array([[ 3,  8, 14, 17],
       [27, 32, 38, 41],
       [51, 56, 62, 65]])

    Здесь начало ядра (по умолчанию) предполагалось в середине фильтра длиной 3. Поэтому каждая входная строка была расширена на одно значение в начале и в конце перед вызовом функции.

    Дополнительно можно определить и передать дополнительные аргументы в функцию фильтра. Эти extra_arguments и extra_keywords аргументы могут использоваться для передачи кортежа дополнительных аргументов и/или словаря именованных аргументов, которые передаются в derivative при каждом вызове. Например, мы можем передать параметры нашего фильтра в качестве аргумента

    >>> def fnc(iline, oline, a, b):
...     oline[...] = iline[:-2] + a * iline[1:-1] + b * iline[2:]
...
>>> generic_filter1d(a, fnc, 3, extra_arguments = (2, 3))
array([[ 3,  8, 14, 17],
       [27, 32, 38, 41],
       [51, 56, 62, 65]])

    или

    >>> generic_filter1d(a, fnc, 3, extra_keywords = {'a':2, 'b':3})
array([[ 3,  8, 14, 17],
       [27, 32, 38, 41],
       [51, 56, 62, 65]])

  • The generic_filter функция реализует общую функцию фильтрации, где фактическая операция фильтрации должна быть предоставлена как функция Python (или другой вызываемый объект). generic_filter функция итерирует по массиву и вызывает function на каждом элементе. Аргумент function является одномерным массивом numpy.float64 тип, который содержит значения вокруг текущего элемента, находящиеся в пределах следа фильтра. Функция должна возвращать единственное значение, которое может быть преобразовано в число двойной точности. Например, рассмотрим корреляцию:

    >>> a = np.arange(12).reshape(3,4)
>>> correlate(a, [[1, 0], [0, 3]])
array([[ 0,  3,  7, 11],
       [12, 15, 19, 23],
       [28, 31, 35, 39]])

    Та же операция может быть реализована с использованием generic_filter, как следует:

    >>> def fnc(buffer):
...     return (buffer * np.array([1, 3])).sum()
...
>>> from scipy.ndimage import generic_filter
>>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]])
array([[ 0,  3,  7, 11],
       [12, 15, 19, 23],
       [28, 31, 35, 39]])

    Здесь было указано ядро, содержащее только два элемента. Поэтому функция фильтра получает буфер длиной равной двум, который был умножен на соответствующие веса и результат суммирован.

    При вызове generic_filter, либо размеры прямоугольного ядра, либо след ядра должны быть предоставлены. размер параметр, если предоставлен, должен быть последовательностью размеров или одним числом, в этом случае размер фильтра считается одинаковым вдоль каждой оси. footprint, если предоставлен, должен быть массивом, который определяет форму ядра своими ненулевыми элементами.

    Дополнительно можно определить и передать дополнительные аргументы в функцию фильтра. Эти extra_arguments и extra_keywords аргументы могут использоваться для передачи кортежа дополнительных аргументов и/или словаря именованных аргументов, которые передаются в derivative при каждом вызове. Например, мы можем передать параметры нашего фильтра в качестве аргумента

    >>> def fnc(buffer, weights):
...     weights = np.asarray(weights)
...     return (buffer * weights).sum()
...
>>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]], extra_arguments = ([1, 3],))
array([[ 0,  3,  7, 11],
       [12, 15, 19, 23],
       [28, 31, 35, 39]])

    или

    >>> generic_filter(a, fnc, footprint = [[1, 0], [0, 1]], extra_keywords= {'weights': [1, 3]})
array([[ 0,  3,  7, 11],
       [12, 15, 19, 23],
       [28, 31, 35, 39]])

Эти функции итерируют по строкам или элементам, начиная с последней оси, т.е. последний индекс изменяется быстрее всего. Такой порядок итерации гарантирован для случаев, когда важно адаптировать фильтр в зависимости от пространственного расположения. Вот пример использования класса, который реализует фильтр и отслеживает текущие координаты во время итерации. Он выполняет ту же операцию фильтрации, что описана выше для generic_filter, но дополнительно выводит текущие координаты:

>>> a = np.arange(12).reshape(3,4)
>>>
>>> class fnc_class:
...     def __init__(self, shape):
...         # store the shape:
...         self.shape = shape
...         # initialize the coordinates:
...         self.coordinates = [0] * len(shape)
...
...     def filter(self, buffer):
...         result = (buffer * np.array([1, 3])).sum()
...         print(self.coordinates)
...         # calculate the next coordinates:
...         axes = list(range(len(self.shape)))
...         axes.reverse()
...         for jj in axes:
...             if self.coordinates[jj] < self.shape[jj] - 1:
...                 self.coordinates[jj] += 1
...                 break
...             else:
...                 self.coordinates[jj] = 0
...         return result
...
>>> fnc = fnc_class(shape = (3,4))
>>> generic_filter(a, fnc.filter, footprint = [[1, 0], [0, 1]])
[0, 0]
[0, 1]
[0, 2]
[0, 3]
[1, 0]
[1, 1]
[1, 2]
[1, 3]
[2, 0]
[2, 1]
[2, 2]
[2, 3]
array([[ 0,  3,  7, 11],
       [12, 15, 19, 23],
       [28, 31, 35, 39]])

Для generic_filter1d функция, тот же подход работает, за исключением того, что эта функция не итерирует по оси, которая фильтруется. Пример для generic_filter1d затем становится этим:

>>> a = np.arange(12).reshape(3,4)
>>>
>>> class fnc1d_class:
...     def __init__(self, shape, axis = -1):
...         # store the filter axis:
...         self.axis = axis
...         # store the shape:
...         self.shape = shape
...         # initialize the coordinates:
...         self.coordinates = [0] * len(shape)
...
...     def filter(self, iline, oline):
...         oline[...] = iline[:-2] + 2 * iline[1:-1] + 3 * iline[2:]
...         print(self.coordinates)
...         # calculate the next coordinates:
...         axes = list(range(len(self.shape)))
...         # skip the filter axis:
...         del axes[self.axis]
...         axes.reverse()
...         for jj in axes:
...             if self.coordinates[jj] < self.shape[jj] - 1:
...                 self.coordinates[jj] += 1
...                 break
...             else:
...                 self.coordinates[jj] = 0
...
>>> fnc = fnc1d_class(shape = (3,4))
>>> generic_filter1d(a, fnc.filter, 3)
[0, 0]
[1, 0]
[2, 0]
array([[ 3,  8, 14, 17],
       [27, 32, 38, 41],
       [51, 56, 62, 65]])

Фильтры в частотной области Фурье#

Функции, описанные в этом разделе, выполняют операции фильтрации в частотной области. Таким образом, входной массив такой функции должен быть совместим с функцией обратного преобразования Фурье, такой как функции из numpy.fft модуля. Поэтому мы должны работать с массивами, которые могут быть результатом вещественного или комплексного преобразования Фурье. В случае вещественного преобразования Фурье сохраняется только половина симметричного комплексного преобразования. Кроме того, необходимо знать длину оси, которая была преобразована вещественным БПФ. Функции, описанные здесь, предоставляют параметр n который, в случае вещественного преобразования, должен быть равен длине оси вещественного преобразования до преобразования. Если этот параметр меньше нуля, предполагается, что входной массив был результатом комплексного преобразования Фурье. Параметр ось может использоваться для указания, вдоль какой оси было выполнено реальное преобразование.

  • The fourier_shift функция умножает входной массив на многомерное преобразование Фурье операции сдвига для заданного сдвига. shift параметр представляет собой последовательность сдвигов для каждого измерения или одно значение для всех измерений.

  • The fourier_gaussian функция умножает входной массив на многомерное преобразование Фурье гауссова фильтра с заданными стандартными отклонениями sigma. sigma параметр представляет собой последовательность значений для каждого измерения или одно значение для всех измерений.

  • The fourier_uniform функция умножает входной массив на многомерное преобразование Фурье равномерного фильтра с заданными размерами размер. размер параметр представляет собой последовательность значений для каждого измерения или одно значение для всех измерений.

  • The fourier_ellipsoid функция умножает входной массив на многомерное преобразование Фурье эллиптического фильтра с заданными размерами размер. размер параметр — это последовательность значений для каждого измерения или одно значение для всех измерений. Эта функция реализована только для измерений 1, 2 и 3.

Функции интерполяции#

В этом разделе описаны различные функции интерполяции, основанные на теории B-сплайнов. Хорошее введение в B-сплайны можно найти в [1] с подробными алгоритмами интерполяции изображений, приведёнными в [5].

Сплайн пре-фильтры#

Интерполяция с использованием сплайнов порядка больше 1 требует шага предварительной фильтрации. Функции интерполяции, описанные в разделе Функции интерполяции применить предварительную фильтрацию, вызвав spline_filter, но их можно настроить так, чтобы они этого не делали, установив параметр prefilter ключевое слово равное False. Это полезно, если более чем одна операция интерполяции выполняется на одном массиве. В этом случае более эффективно выполнить предварительную фильтрацию только один раз и использовать предварительно отфильтрованный массив как вход для функций интерполяции. Следующие две функции реализуют предварительную фильтрацию:

  • The spline_filter1d функция вычисляет одномерный сплайн-фильтр вдоль заданной оси. Выходной массив может быть опционально предоставлен. Порядок сплайна должен быть больше 1 и меньше 6.

  • The spline_filter функция вычисляет многомерный сплайновый фильтр.

    Примечание

    Многомерный фильтр реализован как последовательность одномерных сплайн-фильтров. Промежуточные массивы хранятся в том же типе данных, что и выходные. Поэтому, если запрошен вывод с ограниченной точностью, результаты могут быть неточными, поскольку промежуточные результаты могут храниться с недостаточной точностью. Этого можно избежать, указав выходной тип данных с высокой точностью.

Обработка границ интерполяции#

Все функции интерполяции используют сплайн-интерполяцию для выполнения некоторого типа геометрического преобразования входного массива. Это требует отображения выходных координат на входные координаты, и, следовательно, может возникнуть необходимость в значениях за пределами границ. Эта проблема решается так же, как описано в Функции фильтрации для многомерных функций фильтрации. Поэтому все эти функции поддерживают mode параметр, определяющий, как обрабатываются границы, и cval параметр, который задает постоянное значение в случае использования режима ‘constant’. Поведение всех режимов, включая нецелочисленные позиции, проиллюстрировано ниже. Обратите внимание, что границы обрабатываются не одинаково для всех режимов; reflect (также известный как grid-mirror) и grid-wrap включают симметрию или повторение относительно точки, которая находится на полпути между выборками изображения (пунктирные вертикальные линии), в то время как режимы зеркало и обернуть обрабатывать изображение так, как если бы его границы заканчиваются точно в первой и последней точке выборки, а не на 0.5 выборки дальше.

" "

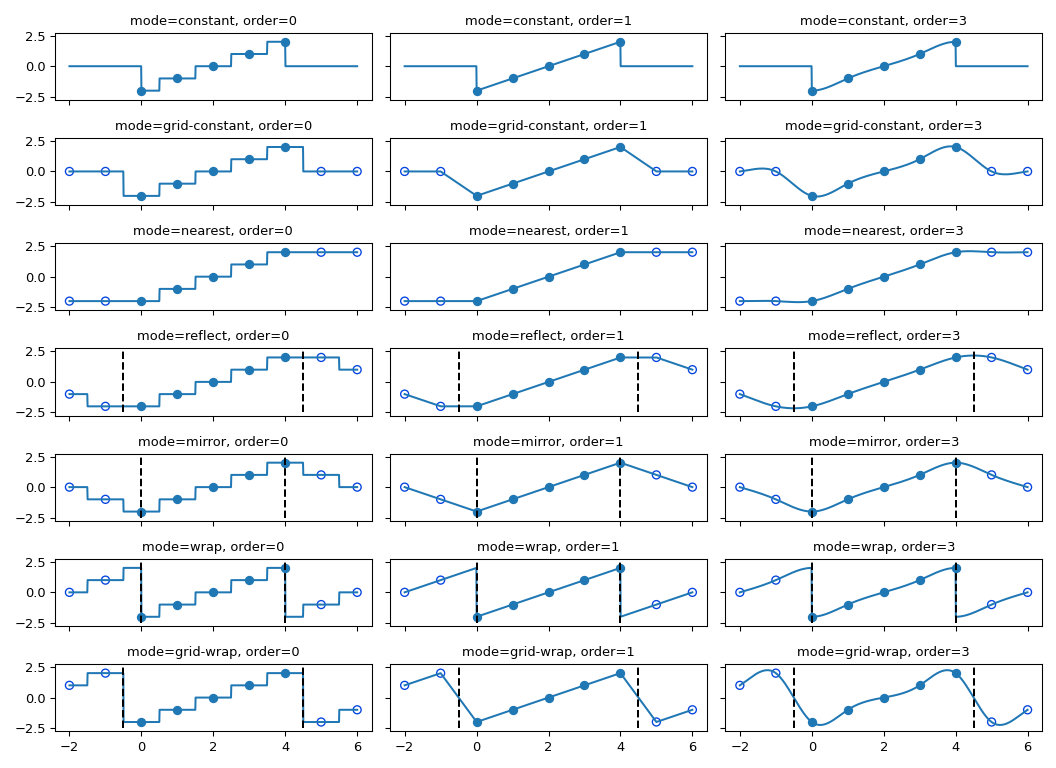
Координаты сэмплов изображения попадают на целочисленные позиции дискретизации в диапазоне от 0 до shape[i] - 1 вдоль каждой оси, iНа рисунке ниже показана интерполяция точки в позиции (3.7, 3.3) внутри изображения формы (7, 7). Для интерполяции порядка n, n + 1 выборки задействованы вдоль каждой оси. Заполненные кружки иллюстрируют местоположения выборок, задействованных в интерполяции значения в местоположении красного x.

" "

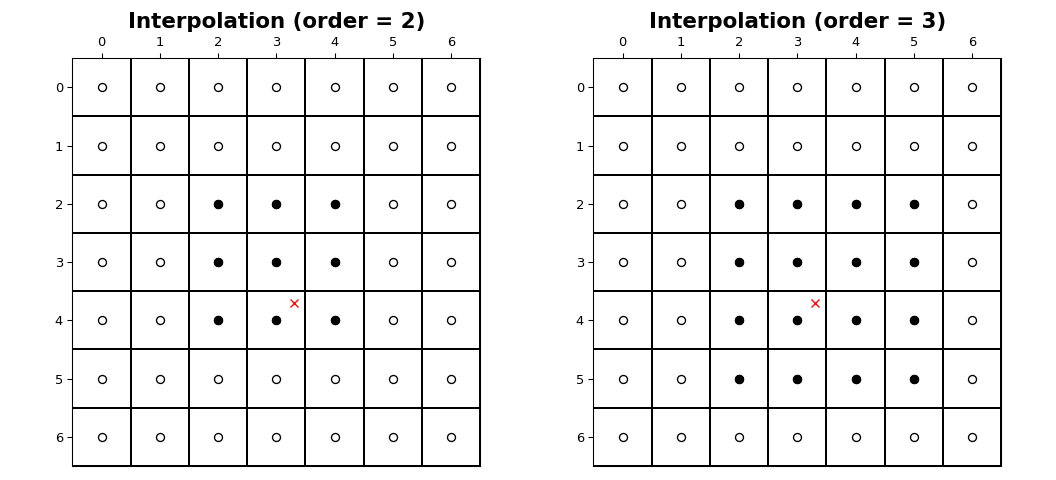
Функции интерполяции#

  • The geometric_transform функция применяет произвольное геометрическое преобразование к входным данным. Заданный mapping функция вызывается в каждой точке вывода для нахождения соответствующих координат во входных данных. mapping должен быть вызываемым объектом, который принимает кортеж длины, равной рангу выходного массива, и возвращает соответствующие входные координаты как кортеж длины, равной рангу входного массива. Выходная форма и выходной тип могут быть предоставлены опционально. Если не указаны, они равны входной форме и типу.

    Например:

    >>> a = np.arange(12).reshape(4,3).astype(np.float64)
>>> def shift_func(output_coordinates):
...     return (output_coordinates[0] - 0.5, output_coordinates[1] - 0.5)
...
>>> from scipy.ndimage import geometric_transform
>>> geometric_transform(a, shift_func)
array([[ 0.    ,  0.    ,  0.    ],
       [ 0.    ,  1.3625,  2.7375],
       [ 0.    ,  4.8125,  6.1875],
       [ 0.    ,  8.2625,  9.6375]])

    Дополнительно можно определить и передать дополнительные аргументы в функцию фильтра. Эти extra_arguments и extra_keywords аргументы могут использоваться для передачи кортежа дополнительных аргументов и/или словаря именованных аргументов, которые передаются в derivative при каждом вызове. Например, мы можем передать сдвиги в нашем примере как аргументы

    >>> def shift_func(output_coordinates, s0, s1):
...     return (output_coordinates[0] - s0, output_coordinates[1] - s1)
...
>>> geometric_transform(a, shift_func, extra_arguments = (0.5, 0.5))
array([[ 0.    ,  0.    ,  0.    ],
       [ 0.    ,  1.3625,  2.7375],
       [ 0.    ,  4.8125,  6.1875],
       [ 0.    ,  8.2625,  9.6375]])

    или

    >>> geometric_transform(a, shift_func, extra_keywords = {'s0': 0.5, 's1': 0.5})
array([[ 0.    ,  0.    ,  0.    ],
       [ 0.    ,  1.3625,  2.7375],
       [ 0.    ,  4.8125,  6.1875],
       [ 0.    ,  8.2625,  9.6375]])

    Примечание

    Функция отображения также может быть написана на C и передана с использованием scipy.LowLevelCallable. См. Расширение scipy.ndimage на C для получения дополнительной информации.

  • Функция map_coordinates применяет произвольное преобразование координат с использованием заданного массива координат. Форма выходных данных определяется формой массива координат путем отбрасывания первой оси. Параметр координаты используется для поиска для каждой точки на выходе соответствующих координат на входе. Значения координаты вдоль первой оси находятся координаты во входном массиве, в которых найдено выходное значение. (См. также numarray координаты функция.) Поскольку координаты могут быть нецелочисленными, значение входных данных в этих координатах определяется сплайн-интерполяцией запрошенного порядка.

    Вот пример, который интерполирует 2D массив в (0.5, 0.5) и (1, 2):

    >>> a = np.arange(12).reshape(4,3).astype(np.float64)
>>> a
array([[  0.,   1.,   2.],
       [  3.,   4.,   5.],
       [  6.,   7.,   8.],
       [  9.,  10.,  11.]])
>>> from scipy.ndimage import map_coordinates
>>> map_coordinates(a, [[0.5, 2], [0.5, 1]])
array([ 1.3625,  7.])

  • The affine_transform функция применяет аффинное преобразование к входному массиву. Заданное преобразование матрица и смещение используются для нахождения для каждой точки вывода соответствующих координат во входных данных. Значение входа в вычисленных координатах определяется сплайн-интерполяцией заказанного порядка. Преобразование матрица должна быть 2-D или также может быть задана как 1-D последовательность или массив. В последнем случае предполагается, что матрица диагональная. Затем применяется более эффективный алгоритм интерполяции, который использует сепарабельность задачи. Форма вывода и тип вывода могут быть указаны опционально. Если не заданы, они равны входной форме и типу.

  • The shift функция возвращает сдвинутую версию ввода, используя сплайн-интерполяцию запрошенного порядок.

  • The zoom функция возвращает масштабированную версию ввода, используя сплайн-интерполяцию запрошенного порядок.

  • The rotate функция возвращает входной массив, повернутый в плоскости, заданной двумя осями, указанными параметром оси, используя сплайн-интерполяцию запрошенного порядок. Угол должен быть задан в градусах. Если reshape истинно, то размер выходного массива адаптируется для содержания повернутого ввода.

Морфология#

Бинарная морфология#

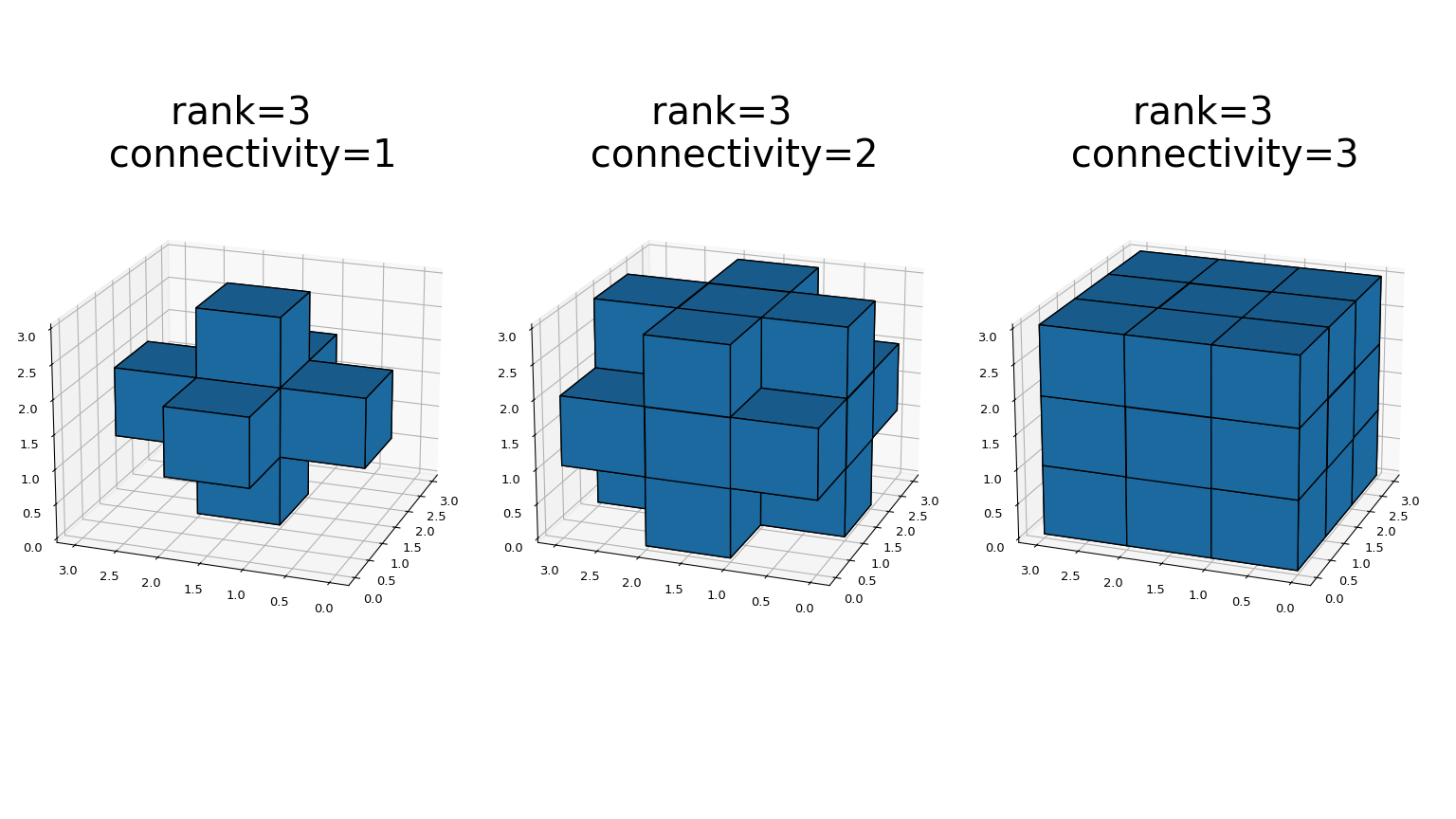
  • The generate_binary_structure функции генерируют бинарный структурирующий элемент для использования в операциях бинарной морфологии. The rank структуры должны быть предоставлены. Размер возвращаемой структуры равен трём в каждом направлении. Значение каждого элемента равно единице, если квадрат евклидова расстояния от элемента до центра меньше или равен связность. Например, 2-D 4-связные и 8-связные структуры генерируются следующим образом:

    >>> from scipy.ndimage import generate_binary_structure
>>> generate_binary_structure(2, 1)
array([[False,  True, False],
       [ True,  True,  True],
       [False,  True, False]], dtype=bool)
>>> generate_binary_structure(2, 2)
array([[ True,  True,  True],
       [ True,  True,  True],
       [ True,  True,  True]], dtype=bool)

Это визуальное представление generate_binary_structure в 3D:

" "

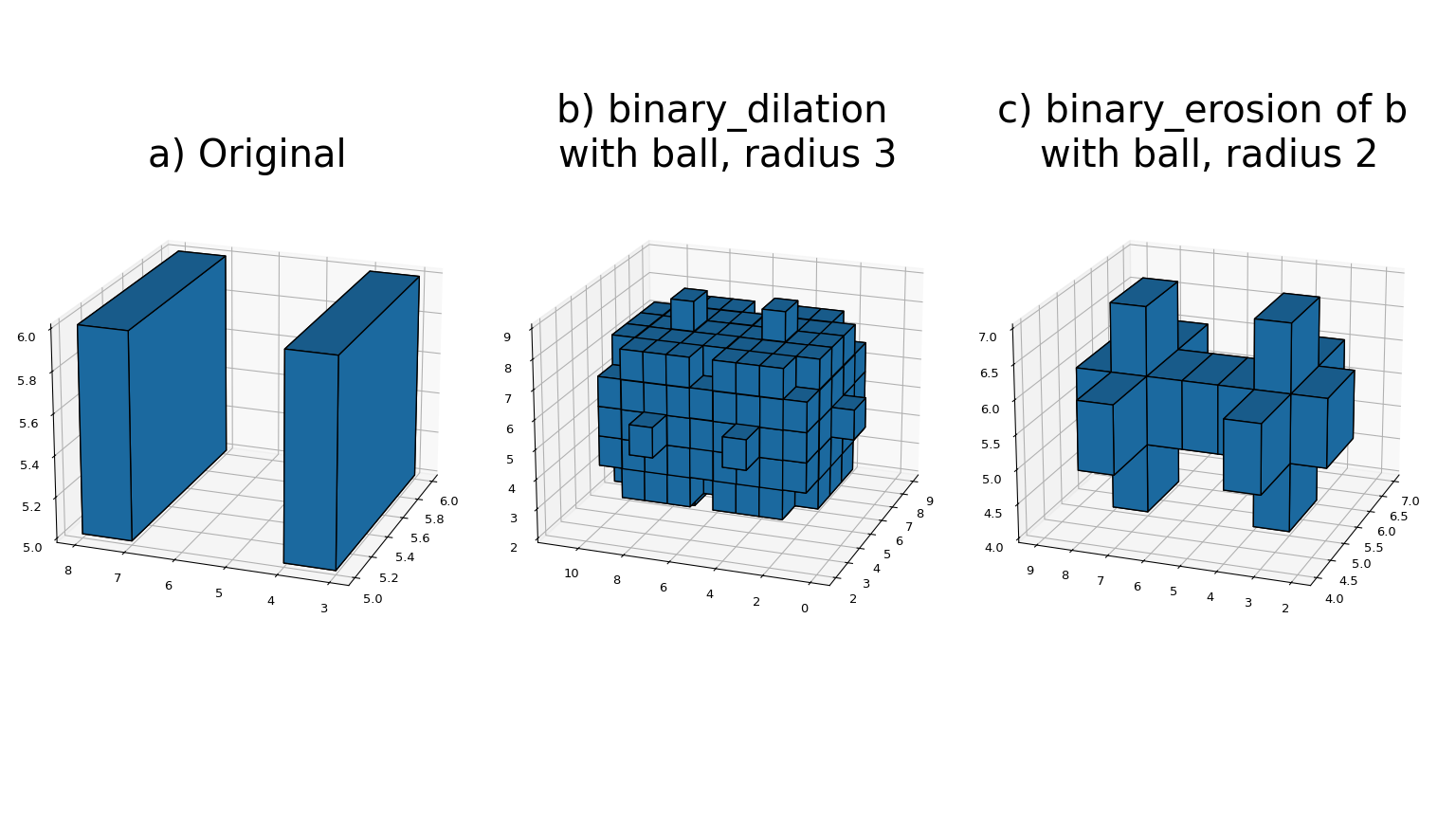
Большинство функций бинарной морфологии могут быть выражены через базовые операции эрозии и дилатации, что можно увидеть здесь:

" "

  • The binary_erosion функция реализует бинарную эрозию массивов произвольного ранга с заданным структурирующим элементом. Параметр origin управляет размещением структурирующего элемента, как описано в Функции фильтрации. Если структурирующий элемент не предоставлен, элемент с связностью, равной единице, генерируется с помощью generate_binary_structure. border_value параметр задаёт значение массива за пределами границ. Эрозия повторяется итерации раз. Если итерации меньше единицы, эрозия повторяется до тех пор, пока результат не перестанет меняться. Если маска если задан массив, только те элементы с истинным значением в соответствующем элементе маски изменяются на каждой итерации.

  • The binary_dilation функция реализует бинарное расширение массивов произвольного ранга с заданным структурирующим элементом. Параметр origin управляет размещением структурирующего элемента, как описано в Функции фильтрации. Если структурирующий элемент не предоставлен, элемент с связностью, равной единице, генерируется с помощью generate_binary_structure. border_value параметр задает значение массива за пределами границ. Дилатация повторяется итерации раз. Если итерации меньше единицы, дилатация повторяется до тех пор, пока результат не перестанет меняться. Если маска если задан массив, только те элементы с истинным значением в соответствующем элементе маски изменяются на каждой итерации.

Вот пример использования binary_dilation найти все элементы, которые касаются границы, путём многократного расширения пустого массива от границы с использованием массива данных в качестве маски:

>>> struct = np.array([[0, 1, 0], [1, 1, 1], [0, 1, 0]])
>>> a = np.array([[1,0,0,0,0], [1,1,0,1,0], [0,0,1,1,0], [0,0,0,0,0]])
>>> a
array([[1, 0, 0, 0, 0],
       [1, 1, 0, 1, 0],
       [0, 0, 1, 1, 0],
       [0, 0, 0, 0, 0]])
>>> from scipy.ndimage import binary_dilation
>>> binary_dilation(np.zeros(a.shape), struct, -1, a, border_value=1)
array([[ True, False, False, False, False],
       [ True,  True, False, False, False],
       [False, False, False, False, False],
       [False, False, False, False, False]], dtype=bool)

The binary_erosion и binary_dilation функции оба имеют итерации параметр, который позволяет повторять эрозию или дилатацию заданное количество раз. Повторение эрозии или дилатации с заданной структурой n раз эквивалентно эрозии или дилатации со структурой, которая n-1 раз расширенную саму с собой. Предоставляется функция, которая позволяет вычислять структуру, расширенную несколько раз самой с собой:

  • The iterate_structure функция возвращает структуру путём дилатации входной структуры итерация - 1 раз с самой собой.

    Например:

    >>> struct = generate_binary_structure(2, 1)
>>> struct
array([[False,  True, False],
       [ True,  True,  True],
       [False,  True, False]], dtype=bool)
>>> from scipy.ndimage import iterate_structure
>>> iterate_structure(struct, 2)
array([[False, False,  True, False, False],
       [False,  True,  True,  True, False],
       [ True,  True,  True,  True,  True],
       [False,  True,  True,  True, False],
       [False, False,  True, False, False]], dtype=bool)

If the origin of the original structure is equal to 0, then it is
also equal to 0 for the iterated structure. If not, the origin
must also be adapted if the equivalent of the *iterations*
erosions or dilations must be achieved with the iterated
structure. The adapted origin is simply obtained by multiplying
with the number of iterations. For convenience, the
:func:`iterate_structure` also returns the adapted origin if the
*origin* parameter is not ``None``:

.. code:: python

   >>> iterate_structure(struct, 2, -1)
   (array([[False, False,  True, False, False],
           [False,  True,  True,  True, False],
           [ True,  True,  True,  True,  True],
           [False,  True,  True,  True, False],
           [False, False,  True, False, False]], dtype=bool), [-2, -2])

Другие морфологические операции могут быть определены через эрозию и дилатацию. Следующие функции предоставляют несколько таких операций для удобства:

  • The binary_opening функция реализует бинарное открытие массивов произвольного ранга с заданным структурирующим элементом. Бинарное открытие эквивалентно бинарной эрозии, за которой следует бинарная дилатация с тем же структурирующим элементом. Параметр origin управляет размещением структурирующего элемента, как описано в Функции фильтрации. Если структурирующий элемент не предоставлен, генерируется элемент со связностью, равной единице, используя generate_binary_structure. итерации параметр задает количество эрозий, выполняемых перед тем же количеством дилатаций.

  • The binary_closing функция реализует бинарное замыкание массивов произвольного ранга с заданным структурирующим элементом. Бинарное замыкание эквивалентно бинарной дилатации, за которой следует бинарная эрозия с тем же структурирующим элементом. Параметр origin управляет размещением структурирующего элемента, как описано в Функции фильтрации. Если структурирующий элемент не предоставлен, генерируется элемент со связностью, равной единице, используя generate_binary_structure. итерации параметр дает количество дилатаций, которые выполняются, за которыми следует то же количество эрозий.

  • The binary_fill_holes функция используется для закрытия отверстий в объектах в бинарном изображении, где структура определяет связность отверстий. Параметр origin управляет размещением структурирующего элемента, как описано в Функции фильтрации. Если структурирующий элемент не предоставлен, генерируется элемент со связностью, равной единице, используя generate_binary_structure.

  • The binary_hit_or_miss функция реализует бинарное преобразование hit-or-miss массивов произвольного ранга с заданными структурирующими элементами. Преобразование hit-or-miss вычисляется эрозией входа с первой структурой, эрозией логического не входных данных со второй структурой, за которым следует логическое и из этих двух эрозий. Параметры origin управляют размещением структурирующих элементов, как описано в Функции фильтрации. Если origin2 равно None, он устанавливается равным origin1 параметр. Если первый структурирующий элемент не предоставлен, структурирующий элемент с связностью, равной единице, генерируется с использованием generate_binary_structure. Если structure2 не предоставлен, он устанавливается равным логическому не of structure1.

Морфология в оттенках серого#

Операции морфологии в оттенках серого являются эквивалентами бинарных морфологических операций, работающих с массивами произвольных значений. Ниже мы описываем эквиваленты в оттенках серого для эрозии, дилатации, открытия и закрытия. Эти операции реализованы аналогично фильтрам, описанным в Функции фильтрации, и мы ссылаемся на этот раздел для описания ядер фильтров и отпечатков, а также обработки границ массивов. Операции морфологии в оттенках серого опционально принимают структура параметр, который дает значения структурного элемента. Если этот параметр не указан, структурный элемент считается плоским со значением, равным нулю. Форма структуры может быть дополнительно определена с помощью footprint параметр. Если этот параметр не задан, структура предполагается прямоугольной с размерами, равными измерениям структура массивом, или с помощью размер параметр если структура не задано. размер параметр используется только если оба структура и footprint не указаны, в этом случае структурирующий элемент предполагается прямоугольным и плоским с размерами, заданными размер. размер параметр, если предоставлен, должен быть последовательностью размеров или единственным числом, в этом случае размер фильтра предполагается одинаковым вдоль каждой оси. Параметр footprint параметр, если предоставлен, должен быть массивом, который определяет форму ядра своими ненулевыми элементами.

Аналогично бинарной эрозии и дилатации, существуют операции для серошкальной эрозии и дилатации:

  • The grey_erosion функция вычисляет многомерную эрозию в оттенках серого.

  • The grey_dilation функция вычисляет многомерное серошкальное расширение.

Операции серого открытия и закрытия могут быть определены аналогично их бинарным аналогам:

  • The grey_opening функция реализует серошкальное открытие массивов произвольного ранга. Серошкальное открытие эквивалентно серошкальной эрозии, за которой следует серошкальное расширение.

  • The grey_closing функция реализует серошкальное замыкание массивов произвольного ранга. Серошкальное открытие эквивалентно серошкальному расширению, за которым следует серошкальное сужение.

  • The morphological_gradient функция реализует градиент серой шкалы морфологии для массивов произвольного ранга. Градиент серой шкалы морфологии равен разности дилатации серой шкалы и эрозии серой шкалы.

  • The morphological_laplace функция реализует серошкальный морфологический лапласиан массивов произвольного ранга. Серошкальный морфологический лапласиан равен сумме серошкальной дилатации и серошкальной эрозии минус удвоенный вход.

  • The white_tophat функция реализует белый top-hat фильтр массивов произвольного ранга. Белый top-hat равен разности входного сигнала и серого открытия.

  • The black_tophat функция реализует черный фильтр "верхняя шляпа" для массивов произвольного ранга. Черная верхняя шляпа равна разности серого замыкания и входных данных.

Дистанционные преобразования#

Преобразования расстояний используются для вычисления минимального расстояния от каждого элемента объекта до фона. Следующие функции реализуют преобразования расстояний для трех различных метрик расстояния: Евклидово расстояние, расстояние городских кварталов и шахматное расстояние.

  • Функция distance_transform_cdt использует алгоритм типа фаски для вычисления преобразования расстояния входных данных, заменяя каждый элемент объекта (определяемый значениями больше нуля) на кратчайшее расстояние до фона (всех необъектных элементов). Структура определяет тип выполняемой фаски. Если структура равна 'cityblock', генерируется структура с использованием generate_binary_structure с квадратом расстояния, равным 1. Если структура равна ‘chessboard’, генерируется структура с использованием generate_binary_structure с квадратом расстояния, равным рангу массива. Эти варианты соответствуют общим интерпретациям метрик расстояния городских кварталов и шахматной доски в двух измерениях.

    В дополнение к преобразованию расстояний можно вычислить преобразование признаков. В этом случае индекс ближайшего фонового элемента возвращается вдоль первой оси результата. The return_distances, и return_indices Флаги могут использоваться для указания, должно ли возвращаться преобразование расстояния, преобразование признаков или оба.

    The расстояния и индексы аргументы могут использоваться для предоставления дополнительных выходных массивов, которые должны быть правильного размера и типа (оба numpy.int32). Основы алгоритма, используемого для реализации этой функции, описаны в [2].

  • Функция distance_transform_edt вычисляет точное евклидово преобразование расстояния входных данных, заменяя каждый элемент объекта (определённый значениями больше нуля) кратчайшим евклидовым расстоянием до фона (всех необъектных элементов).

    В дополнение к преобразованию расстояний можно вычислить преобразование признаков. В этом случае индекс ближайшего фонового элемента возвращается вдоль первой оси результата. The return_distances и return_indices Флаги могут использоваться для указания, должно ли возвращаться преобразование расстояния, преобразование признаков или оба.

    Опционально, выборка вдоль каждой оси может быть задана выборка параметр, который должен быть последовательностью длины, равной рангу входных данных, или одним числом, в этом случае предполагается, что выборка одинакова по всем осям.

    The расстояния и индексы аргументы могут использоваться для предоставления необязательных выходных массивов, которые должны быть правильного размера и типа (numpy.float64 и numpy.int32). Алгоритм, используемый для реализации этой функции, описан в [3].

  • Функция distance_transform_bf использует алгоритм полного перебора для вычисления преобразования расстояния входных данных, путём замены каждого элемента объекта (определяемого значениями больше нуля) на кратчайшее расстояние до фона (всех необъектных элементов). Метрика должна быть одной из "euclidean", "cityblock" или "chessboard".

    В дополнение к преобразованию расстояний можно вычислить преобразование признаков. В этом случае индекс ближайшего фонового элемента возвращается вдоль первой оси результата. The return_distances и return_indices Флаги могут использоваться для указания, должно ли возвращаться преобразование расстояния, преобразование признаков или оба.

    Опционально, выборка вдоль каждой оси может быть задана выборка параметр, который должен быть последовательностью длины, равной рангу ввода, или одиночным числом, при котором выборка предполагается равной по всем осям. Этот параметр используется только в случае евклидова преобразования расстояния.

    The расстояния и индексы аргументы могут использоваться для предоставления необязательных выходных массивов, которые должны быть правильного размера и типа (numpy.float64 и numpy.int32).

    Примечание

    Эта функция использует медленный алгоритм полного перебора, функция distance_transform_cdt может использоваться для более эффективного вычисления преобразований расстояний городских кварталов и шахматной доски. Функция distance_transform_edt может использоваться для более эффективного вычисления точного евклидова преобразования расстояния.

Сегментация и маркировка#

Сегментация — это процесс отделения объектов интереса от фона. Наиболее простой подход — это, вероятно, пороговая обработка по интенсивности, которая легко выполняется с помощью numpy функции:

>>> a = np.array([[1,2,2,1,1,0],
...               [0,2,3,1,2,0],
...               [1,1,1,3,3,2],
...               [1,1,1,1,2,1]])
>>> np.where(a > 1, 1, 0)
array([[0, 1, 1, 0, 0, 0],
       [0, 1, 1, 0, 1, 0],
       [0, 0, 0, 1, 1, 1],
       [0, 0, 0, 0, 1, 0]])

Результат — бинарное изображение, в котором отдельные объекты всё ещё нужно идентифицировать и пометить. Функция label создает массив, где каждому объекту присваивается уникальный номер:

  • The label функция генерирует массив, где объекты во входных данных помечены целочисленным индексом. Она возвращает кортеж, состоящий из массива меток объектов и количества найденных объектов, если только вывод параметр задан, в этом случае возвращается только количество объектов. Связность объектов определяется структурным элементом. Например, в 2D с использованием 4-связного структурного элемента:

    >>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]])
>>> s = [[0, 1, 0], [1,1,1], [0,1,0]]
>>> from scipy.ndimage import label
>>> label(a, s)
(array([[0, 1, 1, 0, 0, 0],
        [0, 1, 1, 0, 2, 0],
        [0, 0, 0, 2, 2, 2],
        [0, 0, 0, 0, 2, 0]], dtype=int32), 2)

    Эти два объекта не связаны, потому что нет способа разместить структурирующий элемент так, чтобы он перекрывался с обоими объектами. Однако 8-связный структурирующий элемент приводит только к одному объекту:

    >>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]])
>>> s = [[1,1,1], [1,1,1], [1,1,1]]
>>> label(a, s)[0]
array([[0, 1, 1, 0, 0, 0],
       [0, 1, 1, 0, 1, 0],
       [0, 0, 0, 1, 1, 1],
       [0, 0, 0, 0, 1, 0]], dtype=int32)

    Если структурирующий элемент не предоставлен, он генерируется вызовом generate_binary_structure (см. Бинарная морфология) с использованием связности один (что в 2D соответствует 4-связной структуре первого примера). Входные данные могут быть любого типа, любое значение, не равное нулю, считается частью объекта. Это полезно, если вам нужно 'перемаркировать' массив индексов объектов, например, после удаления нежелательных объектов. Просто примените функцию маркировки снова к массиву индексов. Например:

    >>> l, n = label([1, 0, 1, 0, 1])
>>> l
array([1, 0, 2, 0, 3], dtype=int32)
>>> l = np.where(l != 2, l, 0)
>>> l
array([1, 0, 0, 0, 3], dtype=int32)
>>> label(l)[0]
array([1, 0, 0, 0, 2], dtype=int32)

    Примечание

    Структурирующий элемент, используемый label предполагается симметричной.

Существует большое количество других подходов к сегментации, например, на основе оценки границ объектов, которые могут быть получены с помощью производных фильтров. Один из таких подходов — сегментация методом водораздела. Функция watershed_ift генерирует массив, где каждому объекту присваивается уникальная метка, из массива, который локализует границы объектов, сгенерированного, например, фильтром градиентной величины. Он использует массив, содержащий начальные маркеры для объектов:

  • The watershed_ift функция применяет алгоритм водораздела от маркеров, используя преобразование Image Foresting Transform, как описано в [4].

  • Входными данными этой функции являются массив, к которому применяется преобразование, и массив маркеров, которые обозначают объекты уникальной меткой, где любое ненулевое значение является маркером. Например:

    >>> input = np.array([[0, 0, 0, 0, 0, 0, 0],
...                   [0, 1, 1, 1, 1, 1, 0],
...                   [0, 1, 0, 0, 0, 1, 0],
...                   [0, 1, 0, 0, 0, 1, 0],
...                   [0, 1, 0, 0, 0, 1, 0],
...                   [0, 1, 1, 1, 1, 1, 0],
...                   [0, 0, 0, 0, 0, 0, 0]], np.uint8)
>>> markers = np.array([[1, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 2, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0]], np.int8)
>>> from scipy.ndimage import watershed_ift
>>> watershed_ift(input, markers)
array([[1, 1, 1, 1, 1, 1, 1],
       [1, 1, 2, 2, 2, 1, 1],
       [1, 2, 2, 2, 2, 2, 1],
       [1, 2, 2, 2, 2, 2, 1],
       [1, 2, 2, 2, 2, 2, 1],
       [1, 1, 2, 2, 2, 1, 1],
       [1, 1, 1, 1, 1, 1, 1]], dtype=int8)

    Здесь два маркера использовались для обозначения объекта (маркер = 2) и фон (маркер = 1). Порядок, в котором они обрабатываются, произволен: перемещение маркера для фона в правый нижний угол массива даёт другой результат:

    >>> markers = np.array([[0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 2, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 1]], np.int8)
>>> watershed_ift(input, markers)
array([[1, 1, 1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1, 1],
       [1, 1, 2, 2, 2, 1, 1],
       [1, 1, 2, 2, 2, 1, 1],
       [1, 1, 2, 2, 2, 1, 1],
       [1, 1, 1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1, 1]], dtype=int8)

    Результат заключается в том, что объект (маркер = 2) меньше, потому что второй маркер был обработан раньше. Это может быть нежелательным эффектом, если первый маркер должен был обозначать фоновый объект. Поэтому, watershed_ift обрабатывает маркеры с отрицательным значением явно как фоновые маркеры и обрабатывает их после обычных маркеров. Например, замена первого маркера на отрицательный маркер даёт результат, аналогичный первому примеру:

    >>> markers = np.array([[0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 2, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, 0],
...                     [0, 0, 0, 0, 0, 0, -1]], np.int8)
>>> watershed_ift(input, markers)
array([[-1, -1, -1, -1, -1, -1, -1],
       [-1, -1,  2,  2,  2, -1, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1, -1,  2,  2,  2, -1, -1],
       [-1, -1, -1, -1, -1, -1, -1]], dtype=int8)

    Связность объектов определяется структурирующим элементом. Если структурирующий элемент не предоставлен, он генерируется вызовом generate_binary_structure (см. Бинарная морфология) используя связность один (что в 2D соответствует 4-связной структуре). Например, использование 8-связной структуры с последним примером даёт другой объект:

    >>> watershed_ift(input, markers,
...               structure = [[1,1,1], [1,1,1], [1,1,1]])
array([[-1, -1, -1, -1, -1, -1, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1,  2,  2,  2,  2,  2, -1],
       [-1, -1, -1, -1, -1, -1, -1]], dtype=int8)

    Примечание

    Реализация watershed_ift ограничивает типы данных входных значений до numpy.uint8 и numpy.uint16.

Измерения объектов#

Для массива размеченных объектов можно измерить свойства отдельных объектов. find_objects функция может использоваться для генерации списка срезов, которые для каждого объекта дают наименьший подмассив, полностью содержащий объект:

  • The find_objects функция находит все объекты в размеченном массиве и возвращает список срезов, соответствующих наименьшим областям в массиве, которые содержат объект.

    Например:

    >>> a = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]])
>>> l, n = label(a)
>>> from scipy.ndimage import find_objects
>>> f = find_objects(l)
>>> a[f[0]]
array([[1, 1],
       [1, 1]])
>>> a[f[1]]
array([[0, 1, 0],
       [1, 1, 1],
       [0, 1, 0]])

    Функция find_objects возвращает срезы для всех объектов, если только не max_label параметр больше нуля, в этом случае только первые max_label объекты возвращаются. Если индекс отсутствует в метка массив, None возвращается вместо среза. Например:

    >>> from scipy.ndimage import find_objects
>>> find_objects([1, 0, 3, 4], max_label = 3)
[(slice(0, 1, None),), None, (slice(2, 3, None),)]

Список срезов, сгенерированный find_objects полезно для нахождения положения и размеров объектов в массиве, но также может использоваться для выполнения измерений на отдельных объектах. Допустим, мы хотим найти сумму интенсивностей объекта на изображении:

>>> image = np.arange(4 * 6).reshape(4, 6)
>>> mask = np.array([[0,1,1,0,0,0],[0,1,1,0,1,0],[0,0,0,1,1,1],[0,0,0,0,1,0]])
>>> labels = label(mask)[0]
>>> slices = find_objects(labels)

Затем мы можем вычислить сумму элементов во втором объекте:

>>> np.where(labels[slices[1]] == 2, image[slices[1]], 0).sum()
80

Однако это не особенно эффективно и также может быть более сложным для других типов измерений. Поэтому определены несколько функций измерений, которые принимают массив меток объектов и индекс объекта, который нужно измерить. Например, вычисление суммы интенсивностей может быть выполнено следующим образом:

>>> from scipy.ndimage import sum as ndi_sum
>>> ndi_sum(image, labels, 2)
80

Для больших массивов и маленьких объектов более эффективно вызывать функции измерений после среза массива:

>>> ndi_sum(image[slices[1]], labels[slices[1]], 2)
80

Альтернативно, мы можем выполнить измерения для нескольких меток с помощью одного вызова функции, возвращая список результатов. Например, чтобы измерить сумму значений фона и второго объекта в нашем примере, мы передаём список меток:

>>> ndi_sum(image, labels, [0, 2])
array([178.0, 80.0])

Все описанные ниже функции измерений поддерживают index параметр для указания, какой объект(ы) должен быть измерен. Значение по умолчанию index является None. Это указывает, что все элементы, где метка больше нуля, должны рассматриваться как единый объект и измеряться. Таким образом, в этом случае метки массив рассматривается как маска, определяемая элементами, которые больше нуля. Если index является числом или последовательностью чисел, он дает метки объектов, которые измеряются. Если index является последовательностью, возвращается список результатов. Функции, возвращающие более одного результата, возвращают свой результат как кортеж, если index является одиночным числом, или как кортеж списков, если index является последовательностью.

  • The sum функция вычисляет сумму элементов объекта с меткой(метками), заданной(заданными) index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки обрабатываются как единый объект. Если метка является None, все элементы входные данные используются в расчете.

  • The mean функция вычисляет среднее элементов объекта с меткой(ами), заданной(ыми) index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки обрабатываются как единый объект. Если метка является None, все элементы входные данные используются в расчете.

  • The variance функция вычисляет дисперсию элементов объекта с меткой(ами), заданной(ыми) index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки рассматриваются как единый объект. Если метка является None, все элементы входные данные используются в вычислениях.

  • The standard_deviation функция вычисляет стандартное отклонение элементов объекта с меткой(ами), заданной(ыми) index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки рассматриваются как единый объект. Если метка является None, все элементы входные данные используются в вычислении.

  • The minimum функция вычисляет минимум элементов объекта с меткой(ами), заданной(ыми) index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки рассматриваются как единый объект. Если метка является None, все элементы входные данные используются в расчете.

  • The maximum функция вычисляет максимум элементов объекта с меткой(метками), заданной(заданными) параметром index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки рассматриваются как единый объект. Если метка является None, все элементы входные данные используются в расчете.

  • The minimum_position функция вычисляет позицию минимума элементов объекта с меткой(ами), заданной(ыми) index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки рассматриваются как единый объект. Если метка является None, все элементы входные данные используются в вычислении.

  • The maximum_position функция вычисляет позицию максимального значения элементов объекта с меткой(метками), заданной(заданными) index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки рассматриваются как единый объект. Если метка является None, все элементы входные данные используются в вычислении.

  • The extrema функция вычисляет минимум, максимум и их позиции для элементов объекта с меткой(метками), заданными index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки рассматриваются как единый объект. Если метка является None, все элементы входные данные используются в вычислениях. Результатом является кортеж, дающий минимум, максимум, позицию минимума и позицию максимума. Результат совпадает с кортежем, образованным результатами функций минимум, maximum, minimum_position, и maximum_position которые описаны выше.

  • The center_of_mass функция вычисляет центр масс объекта с меткой(ами), заданной(ыми) index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки рассматриваются как единый объект. Если метка является None, все элементы входные данные используются в расчете.

  • The histogram функция вычисляет гистограмму объекта с меткой(ами), заданными index, используя метки массив для меток объектов. Если index является None, все элементы с ненулевым значением метки обрабатываются как единый объект. Если метка является None, все элементы входные данные используются в вычислениях. Гистограммы определяются своим минимумом (min), максимум (max), и количество бинов (bins). Они возвращаются как одномерные массивы типа numpy.int32.

Расширение scipy.ndimage на C#

Несколько функций в scipy.ndimage принимает аргумент обратного вызова. Это может быть либо функция Python, либо scipy.LowLevelCallable содержащий указатель на C-функцию. Использование C-функции обычно будет более эффективным, поскольку позволяет избежать накладных расходов на вызов python-функции для многих элементов массива. Чтобы использовать C-функцию, необходимо написать C- расширение, содержащее функцию обратного вызова и Python-функцию, которая возвращает scipy.LowLevelCallable содержащий указатель на callback.

Пример функции, поддерживающей обратные вызовы: geometric_transform, который принимает функцию обратного вызова, определяющую отображение из всех выходных координат в соответствующие координаты во входном массиве. Рассмотрим следующий пример на Python, который использует geometric_transform реализовать функцию сдвига.

from scipy import ndimage

def transform(output_coordinates, shift):
    input_coordinates = output_coordinates[0] - shift, output_coordinates[1] - shift
    return input_coordinates

im = np.arange(12).reshape(4, 3).astype(np.float64)
shift = 0.5
print(ndimage.geometric_transform(im, transform, extra_arguments=(shift,)))

Мы также можем реализовать функцию обратного вызова следующим кодом на C:

/* example.c */

#include 
#include 

static int
_transform(npy_intp *output_coordinates, double *input_coordinates,
           int output_rank, int input_rank, void *user_data)
{
    npy_intp i;
    double shift = *(double *)user_data;

    for (i = 0; i < input_rank; i++) {
        input_coordinates[i] = output_coordinates[i] - shift;
    }
    return 1;
}

static char *transform_signature = "int (npy_intp *, double *, int, int, void *)";

static PyObject *
py_get_transform(PyObject *obj, PyObject *args)
{
    if (!PyArg_ParseTuple(args, "")) return NULL;
    return PyCapsule_New(_transform, transform_signature, NULL);
}

static PyMethodDef ExampleMethods[] = {
    {"get_transform", (PyCFunction)py_get_transform, METH_VARARGS, ""},
    {NULL, NULL, 0, NULL}
};

/* Initialize the module */
static struct PyModuleDef example = {
    PyModuleDef_HEAD_INIT,
    "example",
    NULL,
    -1,
    ExampleMethods,
    NULL,
    NULL,
    NULL,
    NULL
};

PyMODINIT_FUNC
PyInit_example(void)
{
    return PyModule_Create(&example);
}

Дополнительную информацию о написании модулей расширения Python можно найти здесь. Если код на C находится в файле example.cdstemr_lwork> meson.build (см. примеры внутри meson.build файлы) и следуйте тому, что там указано. После этого выполните скрипт:

import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable

from example import get_transform

shift = 0.5

user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable(get_transform(), ptr)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))

дает тот же результат, что и исходный скрипт python.

В версии C, _transform является функцией обратного вызова и параметрами output_coordinates и input_coordinates играют ту же роль, что и в версии на Python, в то время как output_rank и input_rank предоставить эквиваленты len(output_coordinates) и len(input_coordinates). Переменная shift передаётся через user_data вместо extra_arguments. Наконец, функция обратного вызова C возвращает целочисленный статус, который равен единице при успехе и нулю в противном случае.

Функция py_transform оборачивает функцию обратного вызова в PyCapsule. Основные шаги:

  • Инициализировать PyCapsule. Первый аргумент — указатель на функцию обратного вызова.

  • Второй аргумент — сигнатура функции, которая должна точно соответствовать ожидаемой в ndimage.

  • Выше мы использовали scipy.LowLevelCallable чтобы указать user_data который мы сгенерировали с помощью ctypes.

    Другой подход — предоставить данные в контексте капсулы, который может быть установлен с помощью PyCapsule_SetContext и опустить указание user_data в scipy.LowLevelCallable. Однако в этом подходе нам придется иметь дело с выделением/освобождением данных — освобождение данных после уничтожения капсулы может быть выполнено путем указания не-NULL функции обратного вызова в третьем аргументе PyCapsule_New.

C callback-функции для ndimage все следуют этой схеме. В следующем разделе перечислены ndimage функции, которые принимают C функцию обратного вызова и задают прототип функции.

Смотрите также

Функции, которые поддерживают аргументы низкоуровневого обратного вызова:

generic_filter, generic_filter1d, geometric_transform

Ниже мы показываем альтернативные способы написания кода, используя Numba, Cython, ctypes, или cffi вместо написания обёрточного кода на C.

Numba

Numba предоставляет способ легко писать низкоуровневые функции на Python. Мы можем написать вышеуказанное, используя Numba, как:

# example.py
import numpy as np
import ctypes
from scipy import ndimage, LowLevelCallable
from numba import cfunc, types, carray

@cfunc(types.intc(types.CPointer(types.intp),
                  types.CPointer(types.double),
                  types.intc,
                  types.intc,
                  types.voidptr))
def transform(output_coordinates_ptr, input_coordinates_ptr,
              output_rank, input_rank, user_data):
    input_coordinates = carray(input_coordinates_ptr, (input_rank,))
    output_coordinates = carray(output_coordinates_ptr, (output_rank,))
    shift = carray(user_data, (1,), types.double)[0]

    for i in range(input_rank):
        input_coordinates[i] = output_coordinates[i] - shift

    return 1

shift = 0.5

# Then call the function
user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable(transform.ctypes, ptr)

im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))

Cython

Функционально тот же код, что и выше, можно написать на Cython с несколько меньшим количеством шаблонного кода следующим образом:

# example.pyx

from numpy cimport npy_intp as intp

cdef api int transform(intp *output_coordinates, double *input_coordinates,
                       int output_rank, int input_rank, void *user_data):
    cdef intp i
    cdef double shift = (<double *>user_data)[0]

    for i in range(input_rank):
        input_coordinates[i] = output_coordinates[i] - shift
    return 1

# script.py

import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable

import example

shift = 0.5

user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)
callback = LowLevelCallable.from_cython(example, "transform", ptr)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))

cffi

С cffi, вы можете взаимодействовать с C-функцией, находящейся в общей библиотеке (DLL). Сначала нам нужно написать общую библиотеку, что мы делаем на C — этот пример для Linux/OSX:

/*
  example.c
  Needs to be compiled with "gcc -std=c99 -shared -fPIC -o example.so example.c"
  or similar
 */

#include 

int
_transform(intptr_t *output_coordinates, double *input_coordinates,
           int output_rank, int input_rank, void *user_data)
{
    int i;
    double shift = *(double *)user_data;

    for (i = 0; i < input_rank; i++) {
        input_coordinates[i] = output_coordinates[i] - shift;
    }
    return 1;
}

Код Python, вызывающий библиотеку:

import os
import numpy as np
from scipy import ndimage, LowLevelCallable
import cffi

# Construct the FFI object, and copypaste the function declaration
ffi = cffi.FFI()
ffi.cdef("""
int _transform(intptr_t *output_coordinates, double *input_coordinates,
               int output_rank, int input_rank, void *user_data);
""")

# Open library
lib = ffi.dlopen(os.path.abspath("example.so"))

# Do the function call
user_data = ffi.new('double *', 0.5)
callback = LowLevelCallable(lib._transform, user_data)
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))

Вы можете найти больше информации в cffi документация.

ctypes

С ctypes, C-код и компиляция so/DLL такие же, как для cffi выше. Python-код отличается:

# script.py

import os
import ctypes
import numpy as np
from scipy import ndimage, LowLevelCallable

lib = ctypes.CDLL(os.path.abspath('example.so'))

shift = 0.5

user_data = ctypes.c_double(shift)
ptr = ctypes.cast(ctypes.pointer(user_data), ctypes.c_void_p)

# Ctypes has no built-in intptr type, so override the signature
# instead of trying to get it via ctypes
callback = LowLevelCallable(lib._transform, ptr,
    "int _transform(intptr_t *, double *, int, int, void *)")

# Perform the call
im = np.arange(12).reshape(4, 3).astype(np.float64)
print(ndimage.geometric_transform(im, callback))

Вы можете найти больше информации в ctypes документация.

Ссылки#