Преобразования Фурье (scipy.fft)#
Анализ Фурье — это метод представления функции в виде суммы периодических компонентов и восстановления сигнала из этих компонентов. Когда и функция, и её преобразование Фурье заменяются дискретизированными аналогами, это называется дискретным преобразованием Фурье (ДПФ). ДПФ стало основой численных вычислений отчасти благодаря очень быстрому алгоритму его вычисления, называемому быстрым преобразованием Фурье (БПФ), который был известен Гауссу (1805) и был представлен в современной форме Кули и Тьюки. [CT65]. Press et al. [NR07] предоставить доступное введение в анализ Фурье и его приложения.
Быстрое преобразование Фурье#
1-D дискретные преобразования Фурье#
БПФ y[k] длины \(N\) длины\(N\) последовательность x[n] определяется как
и обратное преобразование определяется следующим образом
Эти преобразования могут быть вычислены с помощью fft и ifft,
соответственно, как показано в следующем примере.
>>> from scipy.fft import fft, ifft
>>> import numpy as np
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
>>> y = fft(x)
>>> y
array([ 4.5 +0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j, -1.83155948-1.60822041j,
2.08155948+1.65109876j])
>>> yinv = ifft(y)
>>> yinv
array([ 1.0+0.j, 2.0+0.j, 1.0+0.j, -1.0+0.j, 1.5+0.j])
Из определения БПФ видно, что
В примере
>>> np.sum(x)
4.5
что соответствует \(y[0]\). Для четного N элементы \(y[1]...y[N/2-1]\) содержат положительно-частотные члены, и элементы \(y[N/2]...y[N-1]\) содержат члены с отрицательными частотами в порядке убывания отрицательной частоты. Для нечетного N элементы \(y[1]...y[(N-1)/2]\) содержат положительно-частотные члены, и элементы \(y[(N+1)/2]...y[N-1]\) содержат члены с отрицательными частотами, в порядке убывания отрицательной частоты.
В случае, если последовательность x является вещественной, значения \(y[n]\) для положительных частот является сопряженным к значениям \(y[n]\) для отрицательных частот (поскольку спектр симметричен). Обычно строится только БПФ, соответствующее положительным частотам.
Пример строит БПФ суммы двух синусоид.
>>> from scipy.fft import fft, fftfreq
>>> import numpy as np
>>> # Number of sample points
>>> N = 600
>>> # sample spacing
>>> T = 1.0 / 800.0
>>> x = np.linspace(0.0, N*T, N, endpoint=False)
>>> y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
>>> yf = fft(y)
>>> xf = fftfreq(N, T)[:N//2]
>>> import matplotlib.pyplot as plt
>>> plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
>>> plt.grid()
>>> plt.show()
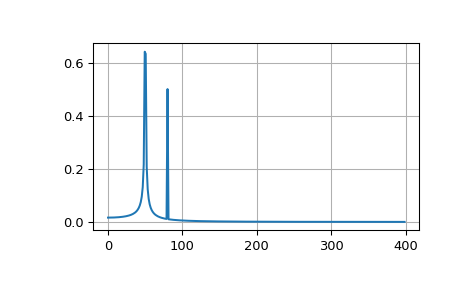
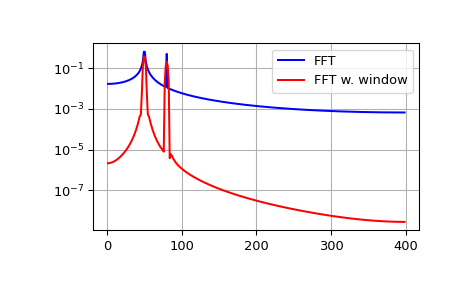
Входной сигнал FFT по своей природе усечен. Это усечение можно смоделировать как умножение бесконечного сигнала на прямоугольную оконную функцию. В спектральной области это умножение становится сверткой спектра сигнала со спектром оконной функции, имеющим форму \(\sin(x)/x\). Эта свертка является причиной эффекта, называемого спектральным просачиванием (см. [WPW]). Оконная обработка сигнала с помощью специальной оконной функции помогает смягчить спектральную утечку. В примере ниже используется окно Блэкмана из scipy.signal и показан эффект оконной обработки (нулевая компонента БПФ была обрезана для наглядности).
>>> from scipy.fft import fft, fftfreq
>>> import numpy as np
>>> # Number of sample points
>>> N = 600
>>> # sample spacing
>>> T = 1.0 / 800.0
>>> x = np.linspace(0.0, N*T, N, endpoint=False)
>>> y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
>>> yf = fft(y)
>>> from scipy.signal.windows import blackman
>>> w = blackman(N)
>>> ywf = fft(y*w)
>>> xf = fftfreq(N, T)[:N//2]
>>> import matplotlib.pyplot as plt
>>> plt.semilogy(xf[1:N//2], 2.0/N * np.abs(yf[1:N//2]), '-b')
>>> plt.semilogy(xf[1:N//2], 2.0/N * np.abs(ywf[1:N//2]), '-r')
>>> plt.legend(['FFT', 'FFT w. window'])
>>> plt.grid()
>>> plt.show()
Если последовательность x комплекснозначная, спектр больше не симметричен. Для упрощения работы с функциями БПФ scipy предоставляет следующие две вспомогательные функции.
Функция fftfreq возвращает точки частоты выборки БПФ.
>>> from scipy.fft import fftfreq
>>> freq = fftfreq(8, 0.125)
>>> freq
array([ 0., 1., 2., 3., -4., -3., -2., -1.])
В аналогичном духе, функция fftshift позволяет менять местами нижнюю и верхнюю половины вектора, чтобы он стал пригодным для отображения.
>>> from scipy.fft import fftshift
>>> x = np.arange(8)
>>> fftshift(x)
array([4, 5, 6, 7, 0, 1, 2, 3])
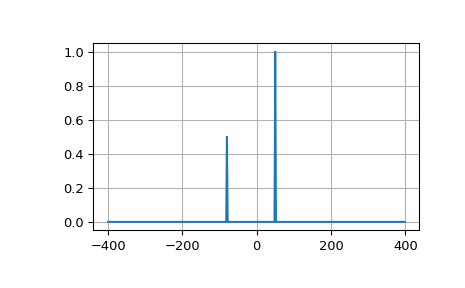
Пример ниже строит график БПФ двух комплексных экспонент; обратите внимание на асимметричный спектр.
>>> from scipy.fft import fft, fftfreq, fftshift
>>> import numpy as np
>>> # number of signal points
>>> N = 400
>>> # sample spacing
>>> T = 1.0 / 800.0
>>> x = np.linspace(0.0, N*T, N, endpoint=False)
>>> y = np.exp(50.0 * 1.j * 2.0*np.pi*x) + 0.5*np.exp(-80.0 * 1.j * 2.0*np.pi*x)
>>> yf = fft(y)
>>> xf = fftfreq(N, T)
>>> xf = fftshift(xf)
>>> yplot = fftshift(yf)
>>> import matplotlib.pyplot as plt
>>> plt.plot(xf, 1.0/N * np.abs(yplot))
>>> plt.grid()
>>> plt.show()
Функция rfft вычисляет БПФ вещественной последовательности и выводит комплексные коэффициенты БПФ \(y[n]\) только для половины диапазона частот.
Оставшиеся компоненты отрицательных частот подразумеваются эрмитовой симметрией
БПФ для вещественного входа (y[n] = conj(y[-n])). В случае чётного N:
\([Re(y[0]) + 0j, y[1], ..., Re(y[N/2]) + 0j]\); в случае, если N нечётное
\([Re(y[0]) + 0j, y[1], ..., y[N/2]\). Явно показанные термины как
\(Re(y[k]) + 0j\) ограничены быть чисто вещественными, поскольку, в силу эрмитовости,
они являются собственными комплексно-сопряженными.
Соответствующая функция irfft вычисляет обратное БПФ коэффициентов БПФ с этим специальным порядком.
>>> from scipy.fft import fft, rfft, irfft
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5, 1.0])
>>> fft(x)
array([ 5.5 +0.j , 2.25-0.4330127j , -2.75-1.29903811j,
1.5 +0.j , -2.75+1.29903811j, 2.25+0.4330127j ])
>>> yr = rfft(x)
>>> yr
array([ 5.5 +0.j , 2.25-0.4330127j , -2.75-1.29903811j,
1.5 +0.j ])
>>> irfft(yr)
array([ 1. , 2. , 1. , -1. , 1.5, 1. ])
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
>>> fft(x)
array([ 4.5 +0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j, -1.83155948-1.60822041j,
2.08155948+1.65109876j])
>>> yr = rfft(x)
>>> yr
array([ 4.5 +0.j , 2.08155948-1.65109876j,
-1.83155948+1.60822041j])
Обратите внимание, что rfft сигналов нечетной и четной длины имеют одинаковую форму.
По умолчанию, irfft предполагает, что выходной сигнал должен быть четной длины. И
поэтому для нечетных сигналов он даст неверный результат:
>>> irfft(yr)
array([ 1.70788987, 2.40843925, -0.37366961, 0.75734049])
Чтобы восстановить исходный сигнал нечётной длины, мы должен передать форму вывода через n параметр.
>>> irfft(yr, n=len(x))
array([ 1. , 2. , 1. , -1. , 1.5])
2- и N-мерные дискретные преобразования Фурье#
Функции fft2 и ifft2 обеспечивают 2-D БПФ и
ОБПФ соответственно. Аналогично, fftn и ifftn предоставляют N-мерное БПФ и обратное БПФ соответственно.
Для сигналов с вещественными входами, аналогично rfft, у нас есть функции
rfft2 и irfft2 для 2-D вещественных преобразований;
rfftn и irfftn для N-D вещественных преобразований.
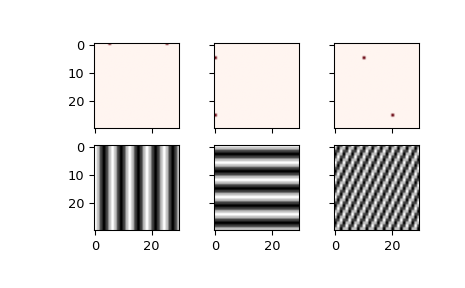
Пример ниже демонстрирует 2-D обратное БПФ и строит график результирующих (2-D) сигналов во временной области.
>>> from scipy.fft import ifftn
>>> import matplotlib.pyplot as plt
>>> import matplotlib.cm as cm
>>> import numpy as np
>>> N = 30
>>> f, ((ax1, ax2, ax3), (ax4, ax5, ax6)) = plt.subplots(2, 3, sharex='col', sharey='row')
>>> xf = np.zeros((N,N))
>>> xf[0, 5] = 1
>>> xf[0, N-5] = 1
>>> Z = ifftn(xf)
>>> ax1.imshow(xf, cmap=cm.Reds)
>>> ax4.imshow(np.real(Z), cmap=cm.gray)
>>> xf = np.zeros((N, N))
>>> xf[5, 0] = 1
>>> xf[N-5, 0] = 1
>>> Z = ifftn(xf)
>>> ax2.imshow(xf, cmap=cm.Reds)
>>> ax5.imshow(np.real(Z), cmap=cm.gray)
>>> xf = np.zeros((N, N))
>>> xf[5, 10] = 1
>>> xf[N-5, N-10] = 1
>>> Z = ifftn(xf)
>>> ax3.imshow(xf, cmap=cm.Reds)
>>> ax6.imshow(np.real(Z), cmap=cm.gray)
>>> plt.show()
Дискретные косинусные преобразования#
SciPy предоставляет DCT с функцией dct и соответствующий ОДПФ
с функцией idct. Существует 8 типов DCT [WPC], [Mak]; однако только первые 4 типа реализованы в scipy. "DCT" обычно относится к DCT типа 2, а "обратный DCT" обычно относится к DCT типа 3. Кроме того, коэффициенты DCT могут быть нормализованы по-разному (для большинства типов scipy предоставляет None и ortho). Два параметра вызовов функций dct/idct
позволяют задать тип DCT и нормализацию коэффициентов.
Для одномерного массива x, dct(x, norm=’ortho’) равен MATLAB dct(x).
DCT типа I#
SciPy использует следующее определение ненормированного DCT-I (norm=None):
Обратите внимание, что DCT-I поддерживается только для размера ввода > 1.
DCT типа II#
SciPy использует следующее определение ненормированного DCT-II
(norm=None):
В случае нормализованного DCT (norm='ortho'), коэффициенты DCT
\(y[k]\) умножаются на масштабный коэффициент f:
В этом случае "базовые функции" DCT \(\phi_k[n] = 2 f \cos \left({\pi(2n+1)k \over 2N} \right)\) становятся ортонормированными:
DCT типа III#
SciPy использует следующее определение ненормированного ДКП-III
(norm=None):
или, для norm='ortho':
DCT типа IV#
SciPy использует следующее определение ненормированного DCT-IV
(norm=None):
или, для norm='ortho':
ДКП и ОДКП#
(ненормированный) DCT-III является обратным к (ненормированному) DCT-II с точностью до
множителя 2N. Ортонормированный DCT-III является точным обратным
ортонормированного DCT-II. Функция idct выполняет отображения между
типами DCT и IDCT, а также правильную нормализацию.
Следующий пример показывает связь между DCT и IDCT для различных типов и нормализаций.
>>> from scipy.fft import dct, idct
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
DCT-II и DCT-III являются обратными друг другу, поэтому для ортонормированного преобразования мы возвращаемся к исходному сигналу.
>>> dct(dct(x, type=2, norm='ortho'), type=3, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
При выполнении того же с нормализацией по умолчанию, однако, мы получаем дополнительный масштабирующий коэффициент \(2N=10\) поскольку прямое преобразование не нормализовано.
>>> dct(dct(x, type=2), type=3)
array([ 10., 20., 10., -10., 15.])
По этой причине мы должны использовать функцию idct используя один и тот же тип для обоих,
давая правильно нормализованный результат.
>>> # Normalized inverse: no scaling factor
>>> idct(dct(x, type=2), type=2)
array([ 1. , 2. , 1. , -1. , 1.5])
Аналогичные результаты можно наблюдать для DCT-I, которая является собственной обратной с точностью до множителя \(2(N-1)\).
>>> dct(dct(x, type=1, norm='ortho'), type=1, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # Unnormalized round-trip via DCT-I: scaling factor 2*(N-1) = 8
>>> dct(dct(x, type=1), type=1)
array([ 8. , 16., 8. , -8. , 12.])
>>> # Normalized inverse: no scaling factor
>>> idct(dct(x, type=1), type=1)
array([ 1. , 2. , 1. , -1. , 1.5])
И для DCT-IV, которая также является своей собственной обратной с точностью до множителя \(2N\).
>>> dct(dct(x, type=4, norm='ortho'), type=4, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # Unnormalized round-trip via DCT-IV: scaling factor 2*N = 10
>>> dct(dct(x, type=4), type=4)
array([ 10., 20., 10., -10., 15.])
>>> # Normalized inverse: no scaling factor
>>> idct(dct(x, type=4), type=4)
array([ 1. , 2. , 1. , -1. , 1.5])
Пример#
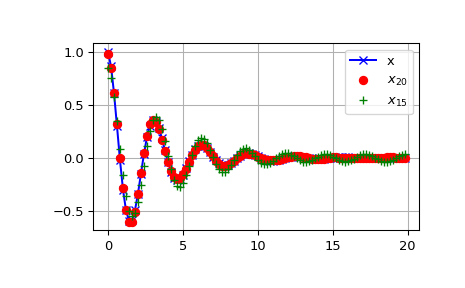
DCT демонстрирует "свойство уплотнения энергии", означающее, что для многих сигналов только первые несколько коэффициентов DCT имеют значительную величину. Обнуление остальных коэффициентов приводит к небольшой ошибке восстановления, что используется в сжатии сигналов с потерями (например, сжатие JPEG).
Пример ниже показывает сигнал x и две реконструкции (\(x_{20}\) и \(x_{15}\)) из коэффициентов ДКП сигнала. Сигнал \(x_{20}\) восстанавливается из первых 20 коэффициентов DCT, \(x_{15}\) восстанавливается из первых 15 коэффициентов ДКП. Видно, что относительная ошибка при использовании 20 коэффициентов всё ещё очень мала (~0.1%), но обеспечивает пятикратную степень сжатия.
>>> from scipy.fft import dct, idct
>>> import matplotlib.pyplot as plt
>>> N = 100
>>> t = np.linspace(0,20,N, endpoint=False)
>>> x = np.exp(-t/3)*np.cos(2*t)
>>> y = dct(x, norm='ortho')
>>> window = np.zeros(N)
>>> window[:20] = 1
>>> yr = idct(y*window, norm='ortho')
>>> sum(abs(x-yr)**2) / sum(abs(x)**2)
0.0009872817275276098
>>> plt.plot(t, x, '-bx')
>>> plt.plot(t, yr, 'ro')
>>> window = np.zeros(N)
>>> window[:15] = 1
>>> yr = idct(y*window, norm='ortho')
>>> sum(abs(x-yr)**2) / sum(abs(x)**2)
0.06196643004256714
>>> plt.plot(t, yr, 'g+')
>>> plt.legend(['x', '$x_{20}$', '$x_{15}$'])
>>> plt.grid()
>>> plt.show()
Дискретные синус-преобразования#
SciPy предоставляет DST [Mak] с функцией dst и соответствующий IDST
с функцией idst.
Теоретически существует 8 типов DST для различных комбинаций чётных/нечётных граничных условий и смещений границ [WPS], только первые 4 типа реализованы в scipy.
DST типа I#
DST-I предполагает, что входные данные нечетны вокруг n=-1 и n=N. SciPy использует следующее
определение ненормированного DST-I (norm=None):
Также обратите внимание, что DST-I поддерживается только для размера входных данных > 1. (Ненормализованный) DST-I является обратным самому себе с точностью до множителя 2(N+1).
DST типа II#
DST-II предполагает, что входные данные нечетны относительно n=-1/2 и четны относительно n=N. SciPy использует следующее определение ненормированного DST-II (norm=None):
DST типа III#
DST-III предполагает, что входные данные нечетны относительно n=-1 и четны относительно n=N-1. SciPy использует следующее определение ненормированного DST-III (norm=None):
DST типа IV#
SciPy использует следующее определение ненормированного DST-IV (norm=None):
или, для norm='ortho':
DST и IDST#
Следующий пример показывает связь между DST и IDST для различных типов и нормализаций.
>>> from scipy.fft import dst, idst
>>> x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
DST-II и DST-III являются обратными друг другу, поэтому для ортонормированного преобразования мы возвращаемся к исходному сигналу.
>>> dst(dst(x, type=2, norm='ortho'), type=3, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
При выполнении того же с нормализацией по умолчанию, однако, мы получаем дополнительный масштабирующий коэффициент \(2N=10\) поскольку прямое преобразование не нормализовано.
>>> dst(dst(x, type=2), type=3)
array([ 10., 20., 10., -10., 15.])
По этой причине мы должны использовать функцию idst используя один и тот же тип для обоих,
давая правильно нормализованный результат.
>>> idst(dst(x, type=2), type=2)
array([ 1. , 2. , 1. , -1. , 1.5])
Аналогичные результаты можно наблюдать для DST-I, который является своим собственным обратным с точностью до коэффициента \(2(N-1)\).
>>> dst(dst(x, type=1, norm='ortho'), type=1, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # scaling factor 2*(N+1) = 12
>>> dst(dst(x, type=1), type=1)
array([ 12., 24., 12., -12., 18.])
>>> # no scaling factor
>>> idst(dst(x, type=1), type=1)
array([ 1. , 2. , 1. , -1. , 1.5])
И для DST-IV, которая также является собственной обратной с точностью до множителя \(2N\).
>>> dst(dst(x, type=4, norm='ortho'), type=4, norm='ortho')
array([ 1. , 2. , 1. , -1. , 1.5])
>>> # scaling factor 2*N = 10
>>> dst(dst(x, type=4), type=4)
array([ 10., 20., 10., -10., 15.])
>>> # no scaling factor
>>> idst(dst(x, type=4), type=4)
array([ 1. , 2. , 1. , -1. , 1.5])
Быстрое преобразование Ханкеля#
SciPy предоставляет функции fht и ifht для выполнения быстрого преобразования Ханкеля (FHT) и его обратного (IFHT) на логарифмически распределенных входных массивах.
FHT — это дискретизированная версия непрерывного преобразования Ханкеля, определённого как [Ham00]
с \(J_{\mu}\) функция Бесселя порядка \(\mu\). При изменении переменных \(r \to \log r\), \(k \to \log k\), это становится
что является сверткой в логарифмическом пространстве. Алгоритм FHT использует FFT для выполнения этой свертки на дискретных входных данных.
Необходимо соблюдать осторожность, чтобы минимизировать числовое кольцевание из-за циклической природы
свертки БПФ. Чтобы обеспечить условие низкого кольцевания [Ham00] выполняется,
выходной массив может быть слегка смещён на смещение, вычисленное с использованием
fhtoffset функция.
Ссылки#
Кули, Джеймс У., и Джон У. Тьюки, 1965, "Алгоритм для машинного вычисления комплексных рядов Фурье," Math. Comput. 19: 297-301.
Press, W., Teukolsky, S., Vetterline, W.T., и Flannery, B.P., 2007, Numerical Recipes: The Art of Scientific Computing, гл. 12-13. Cambridge Univ. Press, Cambridge, UK.
J. Makhoul, 1980, ‘A Fast Cosine Transform in One and Two Dimensions’, IEEE Transactions on acoustics, speech and signal processing т. 28(1), стр. 27-34, DOI:10.1109/TASSP.1980.1163351
A. J. S. Hamilton, 2000, “Uncorrelated modes of the non-linear power spectrum”, MNRAS, 312, 257. DOI:10.1046/j.1365-8711.2000.03071.x