Линейная алгебра (scipy.linalg)

Когда SciPy собран с использованием оптимизированных библиотек ATLAS LAPACK и BLAS, он обладает очень быстрыми возможностями линейной алгебры. Если копнуть достаточно глубоко, все исходные библиотеки LAPACK и BLAS доступны для вашего использования для еще большей скорости. В этом разделе описаны некоторые более простые в использовании интерфейсы к этим процедурам.

Все эти процедуры линейной алгебры ожидают объект, который можно преобразовать в двумерный массив. Результат этих процедур также является двумерным массивом.

scipy.linalg vs numpy.linalg

scipy.linalg содержит все функции из numpy.linalg. плюс некоторые другие более продвинутые, не включённые в numpy.linalg.

Еще одно преимущество использования scipy.linalg над numpy.linalg заключается в том, что он всегда компилируется с поддержкой BLAS/LAPACK, в то время как для NumPy это опционально. Поэтому версия SciPy может быть быстрее в зависимости от того, как был установлен NumPy.

Поэтому, если вы не хотите добавлять scipy как зависимость для вашего numpy программы, используйте scipy.linalg вместо numpy.linalg.

numpy.matrix vs 2-D numpy.ndarray

Классы, представляющие матрицы, и базовые операции, такие как умножение матриц и транспонирование, являются частью numpy. Для удобства мы суммируем различия между numpy.matrix и numpy.ndarray здесь.

numpy.matrix является классом матрицы, который имеет более удобный интерфейс, чем numpy.ndarray для матричных операций. Этот класс поддерживает, например, синтаксис создания, подобный MATLAB, через точку с запятой, имеет матричное умножение по умолчанию для * оператор и содержит I и T члены, которые служат сокращениями для обратной матрицы и транспонирования:

>>> import numpy as np
>>> A = np.asmatrix('[1 2;3 4]')
>>> A
matrix([[1, 2],
        [3, 4]])
>>> A.I
matrix([[-2. ,  1. ],
        [ 1.5, -0.5]])
>>> b = np.asmatrix('[5 6]')
>>> b
matrix([[5, 6]])
>>> b.T
matrix([[5],
        [6]])
>>> A*b.T
matrix([[17],
        [39]])

Несмотря на его удобство, использование numpy.matrix класс не рекомендуется, поскольку он не добавляет ничего, что нельзя было бы сделать с помощью 2-D numpy.ndarray объектов и может привести к путанице в том, какой класс используется. Например, приведённый выше код можно переписать как:

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> linalg.inv(A)
array([[-2. ,  1. ],
      [ 1.5, -0.5]])
>>> b = np.array([[5,6]]) #2D array
>>> b
array([[5, 6]])
>>> b.T
array([[5],
      [6]])
>>> A*b #not matrix multiplication!
array([[ 5, 12],
      [15, 24]])
>>> A.dot(b.T) #matrix multiplication
array([[17],
      [39]])
>>> b = np.array([5,6]) #1D array
>>> b
array([5, 6])
>>> b.T  #not matrix transpose!
array([5, 6])
>>> A.dot(b)  #does not matter for multiplication
array([17, 39])

scipy.linalg операции могут быть применены одинаково к numpy.matrix или к 2D numpy.ndarray объекты.

Базовые процедуры

Нахождение обратной

Обратная матрица \(\mathbf{A}\) является матрицей \(\mathbf{B}\), так что \(\mathbf{AB}=\mathbf{I}\), где \(\mathbf{I}\) является единичной матрицей, состоящей из единиц на главной диагонали. Обычно, \(\mathbf{B}\) обозначается \(\mathbf{B}=\mathbf{A}^{-1}\) . В SciPy обратная матрица массива NumPy, A, получается с использованием linalg.inv (A), или используя A.I if A является матрицей. Например, пусть

\[\begin{split}\mathbf{A} = \left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right],\end{split}\]

затем

\[\begin{split}\mathbf{A^{-1}} = \frac{1}{25} \left[\begin{array}{ccc} -37 & 9 & 22 \\ 14 & 2 & -9 \\ 4 & -3 & 1 \end{array}\right] = % \left[\begin{array}{ccc} -1.48 & 0.36 & 0.88 \\ 0.56 & 0.08 & -0.36 \\ 0.16 & -0.12 & 0.04 \end{array}\right].\end{split}\]

Следующий пример демонстрирует это вычисление в SciPy

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,3,5],[2,5,1],[2,3,8]])
>>> A
array([[1, 3, 5],
      [2, 5, 1],
      [2, 3, 8]])
>>> linalg.inv(A)
array([[-1.48,  0.36,  0.88],
      [ 0.56,  0.08, -0.36],
      [ 0.16, -0.12,  0.04]])
>>> A.dot(linalg.inv(A)) #double check
array([[  1.00000000e+00,  -1.11022302e-16,  -5.55111512e-17],
      [  3.05311332e-16,   1.00000000e+00,   1.87350135e-16],
      [  2.22044605e-16,  -1.11022302e-16,   1.00000000e+00]])

Решение линейной системы

Решение систем линейных уравнений выполняется просто с помощью команды scipy linalg.solve. Эта команда ожидает входную матрицу и вектор правой части. Затем вычисляется вектор решения. Предлагается опция для ввода симметричной матрицы, которая может ускорить обработку, когда применима. В качестве примера предположим, что требуется решить следующие одновременные уравнения:

\begin{eqnarray*} x + 3y + 5z & = & 10 \\ 2x + 5y + z & = & 8 \\ 2x + 3y + 8z & = & 3 \end{eqnarray*}

Мы могли бы найти вектор решения, используя обратную матрицу:

\[\begin{split}\left[\begin{array}{c} x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right]^{-1}\left[\begin{array}{c} 10\\ 8\\ 3\end{array}\right]=\frac{1}{25}\left[\begin{array}{c} -232\\ 129\\ 19\end{array}\right]=\left[\begin{array}{c} -9.28\\ 5.16\\ 0.76\end{array}\right].\end{split}\]

Однако лучше использовать команду linalg.solve, которая может быть быстрее и более численно устойчивой. В этом случае, однако, она дает тот же ответ, как показано в следующем примере:

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1, 2], [3, 4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> b = np.array([[5], [6]])
>>> b
array([[5],
      [6]])
>>> linalg.inv(A).dot(b)  # slow
array([[-4. ],
      [ 4.5]])
>>> A.dot(linalg.inv(A).dot(b)) - b  # check
array([[  8.88178420e-16],
      [  2.66453526e-15]])
>>> np.linalg.solve(A, b)  # fast
array([[-4. ],
      [ 4.5]])
>>> A.dot(np.linalg.solve(A, b)) - b  # check
array([[ 0.],
      [ 0.]])

Нахождение определителя

Определитель квадратной матрицы \(\mathbf{A}\) часто обозначается \(\left|\mathbf{A}\right|\) и является величиной, часто используемой в линейной алгебре. Предположим \(a_{ij}\) являются элементами матрицы \(\mathbf{A}\) и пусть \(M_{ij}=\left|\mathbf{A}_{ij}\right|\) будет определителем матрицы, оставшейся после удаления \(i^{\textrm{th}}\) строка и \(j^{\textrm{th}}\) столбец из \(\mathbf{A}\) . Тогда, для любой строки \(i,\)

\[\left|\mathbf{A}\right|=\sum_{j}\left(-1\right)^{i+j}a_{ij}M_{ij}.\]

Это рекурсивный способ определения определителя, где базовый случай определяется принятием того, что определитель \(1\times1\) матрица является единственным элементом матрицы. В SciPy определитель может быть вычислен с помощью linalg.det. Например, определитель

\[\begin{split}\mathbf{A=}\left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right]\end{split}\]

является

\begin{eqnarray*} \left|\mathbf{A}\right| & = & 1\left|\begin{array}{cc} 5 & 1\\ 3 & 8\end{array}\right|-3\left|\begin{array}{cc} 2 & 1\\ 2 & 8\end{array}\right|+5\left|\begin{array}{cc} 2 & 5\\ 2 & 3\end{array}\right|\\ & = & 1\left(5\cdot8-3\cdot1\right)-3\left(2\cdot8-2\cdot1\right)+5\left(2\cdot3-2\cdot5\right)=-25.\end{eqnarray*}.

В SciPy это вычисляется, как показано в этом примере:

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> linalg.det(A)
-2.0

Вычисление норм

Нормы матриц и векторов также можно вычислять с помощью SciPy. Широкий спектр определений норм доступен с использованием различных параметров для аргумента order в linalg.normЭта функция принимает массив ранга 1 (векторы) или ранга 2 (матрицы) и необязательный аргумент порядка (по умолчанию 2). На основе этих входных данных вычисляется векторная или матричная норма указанного порядка.

Для вектора x, параметр порядка может быть любым действительным числом, включая inf или -inf. Вычисленная норма

\[\begin{split}\left\Vert \mathbf{x}\right\Vert =\left\{ \begin{array}{cc} \max\left|x_{i}\right| & \textrm{ord}=\textrm{inf}\\ \min\left|x_{i}\right| & \textrm{ord}=-\textrm{inf}\\ \left(\sum_{i}\left|x_{i}\right|^{\textrm{ord}}\right)^{1/\textrm{ord}} & \left|\textrm{ord}\right|<\infty.\end{array}\right.\end{split}\]

Для матрицы \(\mathbf{A}\), единственные допустимые значения для norm — \(\pm2,\pm1,\) \(\pm\) inf и 'fro' (или 'f'). Таким образом,

\[\begin{split}\left\Vert \mathbf{A}\right\Vert =\left\{ \begin{array}{cc} \max_{i}\sum_{j}\left|a_{ij}\right| & \textrm{ord}=\textrm{inf}\\ \min_{i}\sum_{j}\left|a_{ij}\right| & \textrm{ord}=-\textrm{inf}\\ \max_{j}\sum_{i}\left|a_{ij}\right| & \textrm{ord}=1\\ \min_{j}\sum_{i}\left|a_{ij}\right| & \textrm{ord}=-1\\ \max\sigma_{i} & \textrm{ord}=2\\ \min\sigma_{i} & \textrm{ord}=-2\\ \sqrt{\textrm{trace}\left(\mathbf{A}^{H}\mathbf{A}\right)} & \textrm{ord}=\textrm{'fro'}\end{array}\right.\end{split}\]

где \(\sigma_{i}\) являются сингулярными значениями \(\mathbf{A}\).

Примеры:

>>> import numpy as np
>>> from scipy import linalg
>>> A=np.array([[1, 2], [3, 4]])
>>> A
array([[1, 2],
      [3, 4]])
>>> linalg.norm(A)
5.4772255750516612
>>> linalg.norm(A, 'fro') # frobenius norm is the default
5.4772255750516612
>>> linalg.norm(A, 1) # L1 norm (max column sum)
6.0
>>> linalg.norm(A, -1)
4.0
>>> linalg.norm(A, np.inf) # L inf norm (max row sum)
7.0

Решение задач линейных наименьших квадратов и псевдообращений

Задачи линейного метода наименьших квадратов возникают во многих разделах прикладной математики. В этой задаче ищется набор линейных масштабирующих коэффициентов, позволяющих модели соответствовать данным. В частности, предполагается, что данные \(y_{i}\) связано с данными \(\mathbf{x}_{i}\) через набор коэффициентов \(c_{j}\) ndarray, ndarray \(f_{j}\left(\mathbf{x}_{i}\right)\) через модель

\[y_{i}=\sum_{j}c_{j}f_{j}\left(\mathbf{x}_{i}\right)+\epsilon_{i},\]

где \(\epsilon_{i}\) представляет неопределенность в данных. Стратегия метода наименьших квадратов заключается в выборе коэффициентов \(c_{j}\) для минимизации

\[J\left(\mathbf{c}\right)=\sum_{i}\left|y_{i}-\sum_{j}c_{j}f_{j}\left(x_{i}\right)\right|^{2}.\]

Теоретически, глобальный минимум будет достигнут, когда

\[\frac{\partial J}{\partial c_{n}^{*}}=0=\sum_{i}\left(y_{i}-\sum_{j}c_{j}f_{j}\left(x_{i}\right)\right)\left(-f_{n}^{*}\left(x_{i}\right)\right)\]

или

\begin{eqnarray*} \sum_{j}c_{j}\sum_{i}f_{j}\left(x_{i}\right)f_{n}^{*}\left(x_{i}\right) & = & \sum_{i}y_{i}f_{n}^{*}\left(x_{i}\right)\\ \mathbf{A}^{H}\mathbf{Ac} & = & \mathbf{A}^{H}\mathbf{y}\end{eqnarray*},

где

\[\left\{ \mathbf{A}\right\} _{ij}=f_{j}\left(x_{i}\right).\]

Когда \(\mathbf{A^{H}A}\) обратима, тогда

\[\mathbf{c}=\left(\mathbf{A}^{H}\mathbf{A}\right)^{-1}\mathbf{A}^{H}\mathbf{y}=\mathbf{A}^{\dagger}\mathbf{y},\]

где \(\mathbf{A}^{\dagger}\) называется псевдообратной к \(\mathbf{A}.\) Обратите внимание, что при использовании этого определения \(\mathbf{A}\) модель может быть записана

\[\mathbf{y}=\mathbf{Ac}+\boldsymbol{\epsilon}.\]

Команда linalg.lstsq решит задачу линейных наименьших квадратов для \(\mathbf{c}\) задан \(\mathbf{A}\) и \(\mathbf{y}\) . Кроме того, linalg.pinv найдёт \(\mathbf{A}^{\dagger}\) задан \(\mathbf{A}.\)

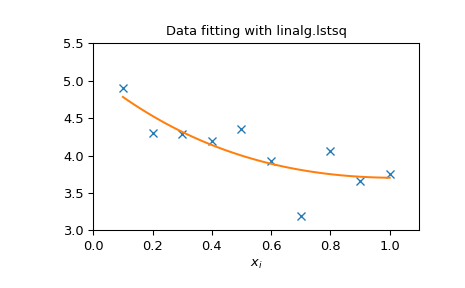
Следующий пример и рисунок демонстрируют использование linalg.lstsq и linalg.pinv для решения задачи аппроксимации данных. Показанные ниже данные были сгенерированы с использованием модели:

\[y_{i}=c_{1}e^{-x_{i}}+c_{2}x_{i},\]

где \(x_{i}=0.1i\) для \(i=1\ldots10\) , \(c_{1}=5\), и \(c_{2}=4.\) Шум добавляется к \(y_{i}\) и коэффициенты \(c_{1}\) и \(c_{2}\) оцениваются с использованием линейного метода наименьших квадратов.

>>> import numpy as np
>>> from scipy import linalg
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

>>> c1, c2 = 5.0, 2.0
>>> i = np.r_[1:11]
>>> xi = 0.1*i
>>> yi = c1*np.exp(-xi) + c2*xi
>>> zi = yi + 0.05 * np.max(yi) * rng.standard_normal(len(yi))

>>> A = np.c_[np.exp(-xi)[:, np.newaxis], xi[:, np.newaxis]]
>>> c, resid, rank, sigma = linalg.lstsq(A, zi)

>>> xi2 = np.r_[0.1:1.0:100j]
>>> yi2 = c[0]*np.exp(-xi2) + c[1]*xi2

>>> plt.plot(xi,zi,'x',xi2,yi2)
>>> plt.axis([0,1.1,3.0,5.5])
>>> plt.xlabel('$x_i$')
>>> plt.title('Data fitting with linalg.lstsq')
>>> plt.show()

Обобщённая обратная

Обобщенная обратная матрица вычисляется с помощью команды linalg.pinv. Пусть \(\mathbf{A}\) быть \(M\times N\) матрица, тогда если \(M>N\), обобщённая обратная матрица это

\[\mathbf{A}^{\dagger}=\left(\mathbf{A}^{H}\mathbf{A}\right)^{-1}\mathbf{A}^{H},\]

в то время как если \(M матрица, обобщённая обратная матрица

\[\mathbf{A}^{\#}=\mathbf{A}^{H}\left(\mathbf{A}\mathbf{A}^{H}\right)^{-1}.\]

В случае, если \(M=N\), затем

\[\mathbf{A}^{\dagger}=\mathbf{A}^{\#}=\mathbf{A}^{-1},\]

до тех пор, пока \(\mathbf{A}\) является обратимой.

Разложения

Во многих приложениях полезно разложить матрицу с использованием других представлений. SciPy поддерживает несколько разложений.

Собственные значения и собственные векторы

Задача на собственные значения и собственные векторы является одной из наиболее часто используемых операций линейной алгебры. В одной популярной форме задача на собственные значения и собственные векторы заключается в нахождении для некоторой квадратной матрицы \(\mathbf{A}\) скаляры \(\lambda\) и соответствующие векторы \(\mathbf{v}\), так что

\[\mathbf{Av}=\lambda\mathbf{v}.\]

Для \(N\times N\) матрица, есть \(N\) (не обязательно различных) собственных значений — корней (характеристического) полинома

\[\left|\mathbf{A}-\lambda\mathbf{I}\right|=0.\]

Собственные векторы, \(\mathbf{v}\), также иногда называются правыми собственными векторами, чтобы отличать их от другого набора левых собственных векторов, удовлетворяющих

\[\mathbf{v}_{L}^{H}\mathbf{A}=\lambda\mathbf{v}_{L}^{H}\]

или

\[\mathbf{A}^{H}\mathbf{v}_{L}=\lambda^{*}\mathbf{v}_{L}.\]

Со своими параметрами по умолчанию, команда linalg.eig возвращает \(\lambda\) и \(\mathbf{v}.\) Однако, он также может возвращать \(\mathbf{v}_{L}\) и просто \(\lambda\) само по себе ( linalg.eigvals возвращает только \(\lambda\) также).

Кроме того, linalg.eig также может решать более общую задачу на собственные значения

\begin{eqnarray*} \mathbf{Av} & = & \lambda\mathbf{Bv}\\ \mathbf{A}^{H}\mathbf{v}_{L} & = & \lambda^{*}\mathbf{B}^{H}\mathbf{v}_{L}\end{eqnarray*}

для квадратных матриц \(\mathbf{A}\) и \(\mathbf{B}.\) Стандартная проблема собственных значений является примером общей проблемы собственных значений для \(\mathbf{B}=\mathbf{I}.\) Когда обобщенная проблема собственных значений может быть решена, она обеспечивает разложение \(\mathbf{A}\) как

\[\mathbf{A}=\mathbf{BV}\boldsymbol{\Lambda}\mathbf{V}^{-1},\]

где \(\mathbf{V}\) представляет собой набор собственных векторов, объединённых в столбцы, \(\boldsymbol{\Lambda}\) является диагональной матрицей собственных значений.

По определению, собственные векторы определены только с точностью до постоянного масштабного множителя. В SciPy масштабный множитель для собственных векторов выбирается так, чтобы \(\left\Vert \mathbf{v}\right\Vert ^{2}=\sum_{i}v_{i}^{2}=1.\)

В качестве примера рассмотрим нахождение собственных значений и собственных векторов матрицы

\[\begin{split}\mathbf{A}=\left[\begin{array}{ccc} 1 & 5 & 2\\ 2 & 4 & 1\\ 3 & 6 & 2\end{array}\right].\end{split}\]

Характеристический полином равен

\begin{eqnarray*} \left|\mathbf{A}-\lambda\mathbf{I}\right| & = & \left(1-\lambda\right)\left[\left(4-\lambda\right)\left(2-\lambda\right)-6\right]-\\ & & 5\left[2\left(2-\lambda\right)-3\right]+2\left[12-3\left(4-\lambda\right)\right]\\ & = & -\lambda^{3}+7\lambda^{2}+8\lambda-3.\end{eqnarray*}

Корни этого полинома являются собственными значениями \(\mathbf{A}\):

\begin{eqnarray*} \lambda_{1} & = & 7.9579\\ \lambda_{2} & = & -1.2577\\ \lambda_{3} & = & 0.2997.\end{eqnarray*}

Собственные векторы, соответствующие каждому собственному значению, можно найти с помощью исходного уравнения. Затем можно найти собственные векторы, связанные с этими собственными значениями.

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1, 2], [3, 4]])
>>> la, v = linalg.eig(A)
>>> l1, l2 = la
>>> print(l1, l2)   # eigenvalues
(-0.3722813232690143+0j) (5.372281323269014+0j)
>>> print(v[:, 0])   # first eigenvector
[-0.82456484  0.56576746]
>>> print(v[:, 1])   # second eigenvector
[-0.41597356 -0.90937671]
>>> print(np.sum(abs(v**2), axis=0))  # eigenvectors are unitary
[1. 1.]
>>> v1 = np.array(v[:, 0]).T
>>> print(linalg.norm(A.dot(v1) - l1*v1))  # check the computation
3.23682852457e-16

Разложение по сингулярным значениям

Сингулярное разложение (SVD) можно рассматривать как расширение проблемы собственных значений на матрицы, не являющиеся квадратными. Пусть \(\mathbf{A}\) быть \(M\times N\) матрица с \(M\) и \(N\) произвольны. Матрицы \(\mathbf{A}^{H}\mathbf{A}\) и \(\mathbf{A}\mathbf{A}^{H}\) являются квадратными эрмитовыми матрицами [1] размера \(N\times N\) и \(M\times M\), соответственно. Известно, что собственные значения квадратных эрмитовых матриц вещественны и неотрицательны. Кроме того, их не более \(\min\left(M,N\right)\) идентичные ненулевые собственные значения \(\mathbf{A}^{H}\mathbf{A}\) и \(\mathbf{A}\mathbf{A}^{H}.\) Определите эти положительные собственные значения как \(\sigma_{i}^{2}.\) Квадратные корни из них называются сингулярными значениями \(\mathbf{A}.\) Собственные векторы \(\mathbf{A}^{H}\mathbf{A}\) собираются по столбцам в \(N\times N\) унитарный [2] матрица \(\mathbf{V}\), в то время как собственные векторы \(\mathbf{A}\mathbf{A}^{H}\) собираются по столбцам в унитарной матрице \(\mathbf{U}\), сингулярные значения собираются в \(M\times N\) нулевая матрица \(\mathbf{\boldsymbol{\Sigma}}\) с главными диагональными элементами, установленными в сингулярные значения. Затем

\[\mathbf{A=U}\boldsymbol{\Sigma}\mathbf{V}^{H}\]

является сингулярным разложением \(\mathbf{A}.\) Каждая матрица имеет сингулярное разложение. Иногда сингулярные значения называют спектром \(\mathbf{A}.\) Команда linalg.svd вернет \(\mathbf{U}\) , \(\mathbf{V}^{H}\), и \(\sigma_{i}\) как массив сингулярных значений. Чтобы получить матрицу \(\boldsymbol{\Sigma}\), используйте linalg.diagsvd. Следующий пример иллюстрирует использование linalg.svd:

>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2,3],[4,5,6]])
>>> A
array([[1, 2, 3],
      [4, 5, 6]])
>>> M,N = A.shape
>>> U,s,Vh = linalg.svd(A)
>>> Sig = linalg.diagsvd(s,M,N)
>>> U, Vh = U, Vh
>>> U
array([[-0.3863177 , -0.92236578],
      [-0.92236578,  0.3863177 ]])
>>> Sig
array([[ 9.508032  ,  0.        ,  0.        ],
      [ 0.        ,  0.77286964,  0.        ]])
>>> Vh
array([[-0.42866713, -0.56630692, -0.7039467 ],
      [ 0.80596391,  0.11238241, -0.58119908],
      [ 0.40824829, -0.81649658,  0.40824829]])
>>> U.dot(Sig.dot(Vh)) #check computation
array([[ 1.,  2.,  3.],
      [ 4.,  5.,  6.]])

[1]

Эрмитова матрица \(\mathbf{D}\) удовлетворяет \(\mathbf{D}^{H}=\mathbf{D}.\)

[2]

Унитарная матрица \(\mathbf{D}\) удовлетворяет \(\mathbf{D}^{H}\mathbf{D}=\mathbf{I}=\mathbf{D}\mathbf{D}^{H}\) так что \(\mathbf{D}^{-1}=\mathbf{D}^{H}.\)

LU-разложение

LU-разложение находит представление для \(M\times N\) матрица \(\mathbf{A}\) как

\[\mathbf{A}=\mathbf{P}\,\mathbf{L}\,\mathbf{U},\]

где \(\mathbf{P}\) является \(M\times M\) матрица перестановки (перестановка строк единичной матрицы), \(\mathbf{L}\) находится в \(M\times K\) нижняя треугольная или трапециевидная матрица ( \(K=\min\left(M,N\right)\)) с единичной диагональю, и \(\mathbf{U}\) является верхней треугольной или трапециевидной матрицей. Команда SciPy для этого разложения — linalg.lu.

Такое разложение часто полезно для решения многих одновременных уравнений, где левая часть не меняется, а правая часть меняется. Например, предположим, что мы собираемся решить

\[\mathbf{A}\mathbf{x}_{i}=\mathbf{b}_{i}\]

для многих различных \(\mathbf{b}_{i}\). LU-разложение позволяет записать это как

\[\mathbf{PLUx}_{i}=\mathbf{b}_{i}.\]

Потому что \(\mathbf{L}\) является нижнетреугольной, уравнение может быть решено для \(\mathbf{U}\mathbf{x}_{i}\) и, наконец, \(\mathbf{x}_{i}\) очень быстро с использованием прямой и обратной подстановки. Начальное время, затраченное на факторизацию \(\mathbf{A}\) позволяет очень быстро решать аналогичные системы уравнений в будущем. Если цель выполнения LU-разложения - решение линейных систем, то команда linalg.lu_factor следует использовать с последующими повторными применениями команды linalg.lu_solve решить систему для каждого нового правого вектора.

Разложение Холецкого

Разложение Холецкого — это частный случай LU-разложения, применимый к эрмитовым положительно определенным матрицам. Когда \(\mathbf{A}=\mathbf{A}^{H}\) и \(\mathbf{x}^{H}\mathbf{Ax}\geq0\) для всех \(\mathbf{x}\), тогда разложения \(\mathbf{A}\) может быть найден так, что

\begin{eqnarray*} \mathbf{A} & = & \mathbf{U}^{H}\mathbf{U}\\ \mathbf{A} & = & \mathbf{L}\mathbf{L}^{H}\end{eqnarray*},

где \(\mathbf{L}\) является нижней треугольной и \(\mathbf{U}\) является верхнетреугольной. Обратите внимание, что \(\mathbf{L}=\mathbf{U}^{H}.\) Команда linalg.cholesky вычисляет разложение Холецкого. Для использования разложения Холецкого для решения систем уравнений также существуют linalg.cho_factor и linalg.cho_solve подпрограммы, которые работают аналогично их аналогам LU-разложения.

QR-разложение

QR-разложение (иногда называемое полярным разложением) работает для любого \(M\times N\) массив и находит \(M\times M\) унитарная матрица \(\mathbf{Q}\) и \(M\times N\) верхняя трапециевидная матрица \(\mathbf{R}\), так что

\[\mathbf{A=QR}.\]

Заметим, что если SVD \(\mathbf{A}\) известно, то можно найти QR-разложение.

\[\mathbf{A}=\mathbf{U}\boldsymbol{\Sigma}\mathbf{V}^{H}=\mathbf{QR}\]

подразумевает, что \(\mathbf{Q}=\mathbf{U}\) и \(\mathbf{R}=\boldsymbol{\Sigma}\mathbf{V}^{H}.\) Однако обратите внимание, что в SciPy для нахождения QR и SVD разложений используются независимые алгоритмы. Команда для QR разложения linalg.qr.

Разложение Шура

Для квадратной \(N\times N\) матрица, \(\mathbf{A}\), разложение Шура находит (не обязательно уникальные) матрицы \(\mathbf{T}\) и \(\mathbf{Z}\), так что

\[\mathbf{A}=\mathbf{ZT}\mathbf{Z}^{H},\]

где \(\mathbf{Z}\) является унитарной матрицей и \(\mathbf{T}\) является либо верхней треугольной, либо квази верхней треугольной, в зависимости от того, запрошена ли вещественная форма Шура или комплексная форма Шура. Для вещественной формы Шура оба \(\mathbf{T}\) и \(\mathbf{Z}\) являются вещественными, когда \(\mathbf{A}\) является вещественным. Когда \(\mathbf{A}\) является вещественной матрицей, вещественная форма Шура только квази верхнетреугольная, потому что \(2\times2\) блоки выступают из главной диагонали, соответствующие любым комплексным собственным значениям. Команда linalg.schur находит разложение Шура, в то время как команда linalg.rsf2csf преобразует \(\mathbf{T}\) и \(\mathbf{Z}\) из вещественной формы Шура в комплексную форму Шура. Форма Шура особенно полезна при вычислении функций от матриц.

Следующий пример иллюстрирует разложение Шура:

>>> from scipy import linalg
>>> A = np.asmatrix('[1 3 2; 1 4 5; 2 3 6]')
>>> T, Z = linalg.schur(A)
>>> T1, Z1 = linalg.schur(A, 'complex')
>>> T2, Z2 = linalg.rsf2csf(T, Z)
>>> T
array([[ 9.90012467,  1.78947961, -0.65498528],
       [ 0.        ,  0.54993766, -1.57754789],
       [ 0.        ,  0.51260928,  0.54993766]])
>>> T2
array([[ 9.90012467+0.00000000e+00j, -0.32436598+1.55463542e+00j,
        -0.88619748+5.69027615e-01j],
       [ 0.        +0.00000000e+00j,  0.54993766+8.99258408e-01j,
         1.06493862+3.05311332e-16j],
       [ 0.        +0.00000000e+00j,  0.        +0.00000000e+00j,
         0.54993766-8.99258408e-01j]])
>>> abs(T1 - T2) # different
array([[  1.06604538e-14,   2.06969555e+00,   1.69375747e+00],  # may vary
       [  0.00000000e+00,   1.33688556e-15,   4.74146496e-01],
       [  0.00000000e+00,   0.00000000e+00,   1.13220977e-15]])
>>> abs(Z1 - Z2) # different
array([[ 0.06833781,  0.88091091,  0.79568503],    # may vary
       [ 0.11857169,  0.44491892,  0.99594171],
       [ 0.12624999,  0.60264117,  0.77257633]])
>>> T, Z, T1, Z1, T2, Z2 = map(np.asmatrix,(T,Z,T1,Z1,T2,Z2))
>>> abs(A - Z*T*Z.H)  # same
matrix([[  5.55111512e-16,   1.77635684e-15,   2.22044605e-15],
        [  0.00000000e+00,   3.99680289e-15,   8.88178420e-16],
        [  1.11022302e-15,   4.44089210e-16,   3.55271368e-15]])
>>> abs(A - Z1*T1*Z1.H)  # same
matrix([[  4.26993904e-15,   6.21793362e-15,   8.00007092e-15],
        [  5.77945386e-15,   6.21798014e-15,   1.06653681e-14],
        [  7.16681444e-15,   8.90271058e-15,   1.77635764e-14]])
>>> abs(A - Z2*T2*Z2.H)  # same
matrix([[  6.02594127e-16,   1.77648931e-15,   2.22506907e-15],
        [  2.46275555e-16,   3.99684548e-15,   8.91642616e-16],
        [  8.88225111e-16,   8.88312432e-16,   4.44104848e-15]])

Интерполяционное разложение

scipy.linalg.interpolative содержит подпрограммы для вычисления интерполяционного разложения (ID) матрицы. Для матрицы \(A \in \mathbb{C}^{m \times n}\) ранга \(k \leq \min \{ m, n \}\) это факторизация

\[A \Pi = \begin{bmatrix} A \Pi_{1} & A \Pi_{2} \end{bmatrix} = A \Pi_{1} \begin{bmatrix} I & T \end{bmatrix},\]

где \(\Pi = [\Pi_{1}, \Pi_{2}]\) является матрицей перестановки с \(\Pi_{1} \in \{ 0, 1 \}^{n \times k}\), т.е., \(A \Pi_{2} = A \Pi_{1} T\). Это может быть эквивалентно записано как \(A = BP\), где \(B = A \Pi_{1}\) и \(P = [I, T] \Pi^{\mathsf{T}}\) являются скелет и интерполяционные матрицы, соответственно.

Смотрите также

scipy.linalg.interpolative — для получения дополнительной информации.

Матричные функции

Рассмотрим функцию \(f\left(x\right)\) с разложением в ряд Тейлора

\[f\left(x\right)=\sum_{k=0}^{\infty}\frac{f^{\left(k\right)}\left(0\right)}{k!}x^{k}.\]

Матричная функция может быть определена с использованием этого ряда Тейлора для квадратной матрицы \(\mathbf{A}\) как

\[f\left(\mathbf{A}\right)=\sum_{k=0}^{\infty}\frac{f^{\left(k\right)}\left(0\right)}{k!}\mathbf{A}^{k}.\]

Примечание

Хотя это служит полезным представлением матричной функции, редко это лучший способ вычисления матричной функции. В частности, если матрица не диагонализируема, результаты могут быть неточными.

Экспоненциальные и логарифмические функции

Матричная экспонента — одна из наиболее распространённых матричных функций. Предпочтительный метод реализации матричной экспоненты — использование масштабирования и аппроксимации Паде для \(e^{x}\). Этот алгоритм реализован как linalg.expm.

Обратной матричной экспоненте является матричный логарифм, определённый как обратная матричная экспонента:

\[\mathbf{A}\equiv\exp\left(\log\left(\mathbf{A}\right)\right).\]

Матричный логарифм может быть получен с помощью linalg.logm.

Тригонометрические функции

Тригонометрические функции, \(\sin\), \(\cos\), и \(\tan\), реализованы для матриц в linalg.sinm, linalg.cosm, и linalg.tanm, соответственно. Матричный синус и косинус могут быть определены с использованием тождества Эйлера как

\begin{eqnarray*} \sin\left(\mathbf{A}\right) & = & \frac{e^{j\mathbf{A}}-e^{-j\mathbf{A}}}{2j}\\ \cos\left(\mathbf{A}\right) & = & \frac{e^{j\mathbf{A}}+e^{-j\mathbf{A}}}{2}.\end{eqnarray*}

Тангенс равен

\[\tan\left(x\right)=\frac{\sin\left(x\right)}{\cos\left(x\right)}=\left[\cos\left(x\right)\right]^{-1}\sin\left(x\right)\]

и поэтому матричный тангенс определяется как

\[\left[\cos\left(\mathbf{A}\right)\right]^{-1}\sin\left(\mathbf{A}\right).\]

Гиперболические тригонометрические функции

Гиперболические тригонометрические функции, \(\sinh\), \(\cosh\), и \(\tanh\), также может быть определена для матриц с использованием знакомых определений:

\begin{eqnarray*} \sinh\left(\mathbf{A}\right) & = & \frac{e^{\mathbf{A}}-e^{-\mathbf{A}}}{2}\\ \cosh\left(\mathbf{A}\right) & = & \frac{e^{\mathbf{A}}+e^{-\mathbf{A}}}{2}\\ \tanh\left(\mathbf{A}\right) & = & \left[\cosh\left(\mathbf{A}\right)\right]^{-1}\sinh\left(\mathbf{A}\right).\end{eqnarray*}

Эти матричные функции можно найти с помощью linalg.sinhm, linalg.coshm, и linalg.tanhm.

Произвольная функция

Наконец, любая произвольная функция, которая принимает одно комплексное число и возвращает комплексное число, может быть вызвана как матричная функция с помощью команды linalg.funm. Эта команда принимает матрицу и произвольную функцию Python. Затем она реализует алгоритм из книги Голуба и Ван Лоана "Matrix Computations" для вычисления функции, применённой к матрице с использованием разложения Шура. Обратите внимание, что функция должна принимать комплексные числа в качестве входных данных для работы с этим алгоритмом. Например, следующий код вычисляет функцию Бесселя нулевого порядка, примененную к матрице.

>>> from scipy import special, linalg
>>> rng = np.random.default_rng()
>>> A = rng.random((3, 3))
>>> B = linalg.funm(A, lambda x: special.jv(0, x))
>>> A
array([[0.06369197, 0.90647174, 0.98024544],
       [0.68752227, 0.5604377 , 0.49142032],
       [0.86754578, 0.9746787 , 0.37932682]])
>>> B
array([[ 0.6929219 , -0.29728805, -0.15930896],
       [-0.16226043,  0.71967826, -0.22709386],
       [-0.19945564, -0.33379957,  0.70259022]])
>>> linalg.eigvals(A)
array([ 1.94835336+0.j, -0.72219681+0.j, -0.22270006+0.j])
>>> special.jv(0, linalg.eigvals(A))
array([0.25375345+0.j, 0.87379738+0.j, 0.98763955+0.j])
>>> linalg.eigvals(B)
array([0.25375345+0.j, 0.87379738+0.j, 0.98763955+0.j])

Обратите внимание, как, в силу определения матричных аналитических функций, функция Бесселя подействовала на собственные значения матрицы.

Специальные матрицы

SciPy и NumPy предоставляют несколько функций для создания специальных матриц, которые часто используются в инженерии и науке.

Тип	Функция	Описание
блочно-диагональная	scipy.linalg.block_diag	Создать блочно-диагональную матрицу из предоставленных массивов.
circulant	scipy.linalg.circulant	Создать циркулянтную матрицу.
компаньон	scipy.linalg.companion	Создать сопровождающую матрицу.
свёртка	scipy.linalg.convolution_matrix	Создать матрицу свертки.
Дискретное преобразование Фурье	scipy.linalg.dft	Создать матрицу дискретного преобразования Фурье.
Фидлер	scipy.linalg.fiedler	Создать симметричную матрицу Фиделера.
Fiedler Companion	scipy.linalg.fiedler_companion	Создать матрицу-компаньон Фидлера.
Адамар	scipy.linalg.hadamard	Создать матрицу Адамара.
Ганкель	scipy.linalg.hankel	Создать матрицу Ганкеля.
Гельмерт	scipy.linalg.helmert	Создать матрицу Хельмерта.
Гильберт	scipy.linalg.hilbert	Создать матрицу Гильберта.
Обратное преобразование Гильберта	scipy.linalg.invhilbert	Создание обратной матрицы Гильберта.
Leslie	scipy.linalg.leslie	Создать матрицу Лесли.
Паскаль	scipy.linalg.pascal	Создать матрицу Паскаля.
Обратный Паскаль	scipy.linalg.invpascal	Создать обратную матрицу Паскаля.
Toeplitz	scipy.linalg.toeplitz	Создать матрицу Тёплица.
Ван дер Монд	numpy.vander	Создать матрицу Вандермонда.

Примеры использования этих функций см. в их соответствующих строках документации.

Расширенные возможности

Поддержка пакетной обработки

Некоторые линейные алгебраические функции SciPy могут обрабатывать пакеты скаляров, 1D- или 2D-массивов, заданных N-мерным массивом на входе. Например, линейная алгебраическая функция, которая обычно принимает (2D) матрицу, может принимать массив формы (4, 3, 2), что он интерпретировал бы как пакет из четырёх матриц 3 на 2. В этом случае мы говорим, что основная форма входа равно (3, 2) и форма пакета является (4,). Аналогично, функция линейной алгебры, которая обычно принимает вектор (1D), будет обрабатывать (4, 3, 2) массив как (4, 3) пакет векторов, в этом случае основная форма входных данных (2,) и форма пакета является (4, 3). Длина основной формы также называется основное измерение. В этих случаях итоговая форма вывода — это пакетная форма ввода, объединённая с основной формой вывода (т.е. формой вывода, когда пакетная форма ввода равна ()). Для получения дополнительной информации см. Пакетные линейные операции.