numpy.bartlett

numpy.bartlett(M)

Возвращает окно Бартлетта.

Окно Бартлетта очень похоже на треугольное окно, за исключением того, что конечные точки находятся на нуле. Оно часто используется в обработке сигналов для сужения сигнала без создания слишком большого колебания в частотной области.

Параметры:

Mint

Количество точек в выходном окне. Если ноль или меньше, возвращается пустой массив.

Возвращает:

выходмассив

Треугольное окно, с максимальным значением, нормализованным к единице (значение один появляется только если количество выборок нечетное), с первой и последней выборками, равными нулю.

Смотрите также

blackman, hamming, hanning, kaiser

Примечания

Окно Бартлетта определяется как

\[w(n) = \frac{2}{M-1} \left( \frac{M-1}{2} - \left|n - \frac{M-1}{2}\right| \right)\]

Большинство ссылок на окно Бартлетта происходят из литературы по обработке сигналов, где оно используется как одна из многих оконных функций для сглаживания значений. Обратите внимание, что свёртка с этим окном даёт линейную интерполяцию. Оно также известно как аподизация (что означает «удаление ноги», т.е. сглаживание разрывов в начале и конце дискретизированного сигнала) или сужающая функция. Преобразование Фурье окна Бартлетта является произведением двух функций sinc. Обратите внимание на отличное обсуждение в Kanasewich [2].

Ссылки

[1]

M.S. Bartlett, «Periodogram Analysis and Continuous Spectra», Biometrika 37, 1-16, 1950.

[2]

E.R. Kanasewich, «Time Sequence Analysis in Geophysics», The University of Alberta Press, 1975, стр. 109-110.

[3]

A.V. Oppenheim и R.W. Schafer, «Discrete-Time Signal Processing», Prentice-Hall, 1999, стр. 468-471.

[4]

Википедия, "Оконная функция", https://en.wikipedia.org/wiki/Window_function

[5]

W.H. Press, B.P. Flannery, S.A. Teukolsky и W.T. Vetterling, «Numerical Recipes», Cambridge University Press, 1986, страница 429.

Примеры

Попробуйте в вашем браузере!

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> np.bartlett(12)
array([ 0.        ,  0.18181818,  0.36363636,  0.54545455,  0.72727273, # may vary
        0.90909091,  0.90909091,  0.72727273,  0.54545455,  0.36363636,
        0.18181818,  0.        ])

Постройте окно и его частотную характеристику (требует SciPy и matplotlib).

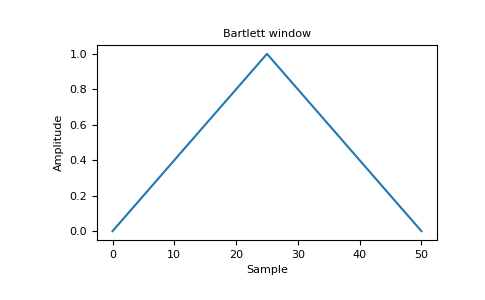
import matplotlib.pyplot as plt
from numpy.fft import fft, fftshift
window = np.bartlett(51)
plt.plot(window)
plt.title("Bartlett window")
plt.ylabel("Amplitude")
plt.xlabel("Sample")
plt.show()

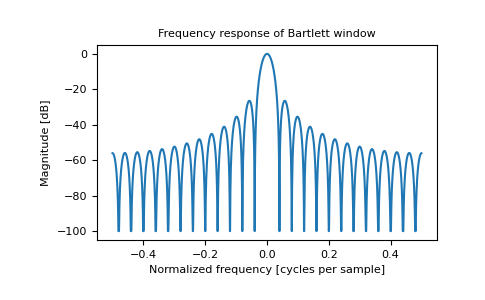
plt.figure()
A = fft(window, 2048) / 25.5
mag = np.abs(fftshift(A))
freq = np.linspace(-0.5, 0.5, len(A))
with np.errstate(divide='ignore', invalid='ignore'):
    response = 20 * np.log10(mag)
response = np.clip(response, -100, 100)
plt.plot(freq, response)
plt.title("Frequency response of Bartlett window")
plt.ylabel("Magnitude [dB]")
plt.xlabel("Normalized frequency [cycles per sample]")
plt.axis('tight')
plt.show()

НазадОткрыть во вкладке