numpy.hamming#

numpy.hamming(M)[источник]#

Возвращает окно Хэмминга.

Окно Хэмминга - это сужение, образованное с использованием взвешенного косинуса.

Параметры:

Mint: Количество точек в выходном окне. Если ноль или меньше, возвращается пустой массив.

Возвращает:

выходndarray: Окно с максимальным значением, нормализованным до единицы (значение единица появляется только если количество выборок нечётное).

Смотрите также

bartlett, blackman, hanning, kaiser

Примечания

Окно Хэмминга определяется как

\[w(n) = 0.54 - 0.46\cos\left(\frac{2\pi{n}}{M-1}\right) \qquad 0 \leq n \leq M-1\]

Окно Хэмминга названо в честь Р. В. Хэмминга, коллеги Дж. В. Тьюки, и описано у Блэкмана и Тьюки. Оно рекомендовалось для сглаживания усечённой автоковариационной функции во временной области. Большинство ссылок на окно Хэмминга происходит из литературы по обработке сигналов, где оно используется как одна из многих оконных функций для сглаживания значений. Также известно как аподизация (что означает «удаление ноги», т.е. сглаживание разрывов в начале и конце дискретизированного сигнала) или сужающая функция.

Ссылки

[1]

Блэкман, Р.Б. и Тьюки, Дж.В., (1958) Измерение спектров мощности, Dover Publications, Нью-Йорк.

[2]

E.R. Kanasewich, "Time Sequence Analysis in Geophysics", The University of Alberta Press, 1975, pp. 109-110.

[3]

Википедия, "Оконная функция", https://en.wikipedia.org/wiki/Window_function

[4]

У.Х. Пресс, Б.П. Флэннери, С.А. Тьюколски и У.Т. Веттерлинг, «Численные рецепты», Cambridge University Press, 1986, страница 425.

Примеры

>>> import numpy as np
>>> np.hamming(12)
array([ 0.08      ,  0.15302337,  0.34890909,  0.60546483,  0.84123594, # may vary
        0.98136677,  0.98136677,  0.84123594,  0.60546483,  0.34890909,
        0.15302337,  0.08      ])

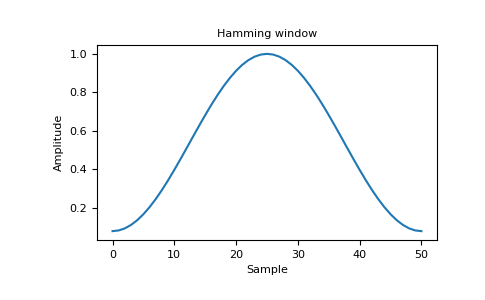
Построить график окна и частотной характеристики.

import matplotlib.pyplot as plt
from numpy.fft import fft, fftshift
window = np.hamming(51)
plt.plot(window)
plt.title("Hamming window")
plt.ylabel("Amplitude")
plt.xlabel("Sample")
plt.show()

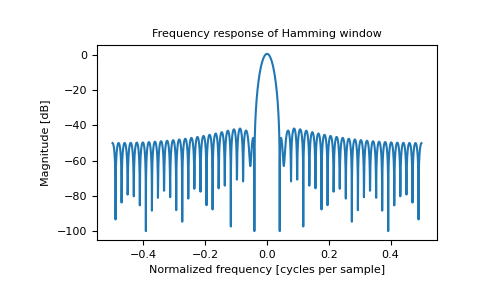
plt.figure()
A = fft(window, 2048) / 25.5
mag = np.abs(fftshift(A))
freq = np.linspace(-0.5, 0.5, len(A))
response = 20 * np.log10(mag)
response = np.clip(response, -100, 100)
plt.plot(freq, response)
plt.title("Frequency response of Hamming window")
plt.ylabel("Magnitude [dB]")
plt.xlabel("Normalized frequency [cycles per sample]")
plt.axis('tight')
plt.show()