Тест Даннетта#
Тест Даннетта сравнивает средние значения нескольких экспериментальных групп с одной контрольной группой. В [1], исследуется влияние лекарств на измерения количества клеток крови в трех группах животных.
В следующей таблице приведены результаты эксперимента, в котором две группы получали разные препараты, а одна группа выступала в качестве контроля. Подсчеты клеток крови (в миллионах клеток на кубический миллиметр) были записаны:
import numpy as np
control = np.array([7.40, 8.50, 7.20, 8.24, 9.84, 8.32])
drug_a = np.array([9.76, 8.80, 7.68, 9.36])
drug_b = np.array([12.80, 9.68, 12.16, 9.20, 10.55])
Мы хотели бы проверить, различаются ли средние значения между любыми из групп статистически значимо. Сначала визуально исследуем диаграмму размаха.
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
ax.boxplot([control, drug_a, drug_b])
ax.set_xticklabels(["Control", "Drug A", "Drug B"])
ax.set_ylabel("mean")
plt.show()
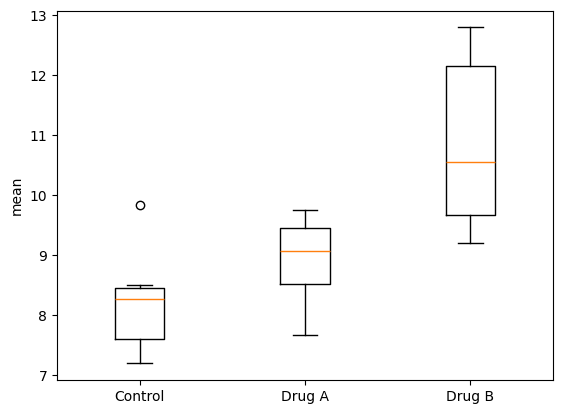
Обратите внимание на перекрывающиеся межквартильные размахи группы препарата A и контрольной группы и явное разделение между группой препарата B и контрольной группой.
Далее мы будем использовать Dunnett's test для оценки, является ли
разница между средними групп значимой при контроле
уровня ошибки по семейству: вероятности совершения любых ложных открытий.
Пусть нулевая гипотеза состоит в том, что экспериментальные группы имеют то же среднее, что и контрольная группа, а альтернативная — что экспериментальная группа не имеет того же среднего, что и контрольная. Мы считаем приемлемой 5% частоту ошибок для семейства и поэтому выбираем 0.05 в качестве порога значимости.
from scipy.stats import dunnett
res = dunnett(drug_a, drug_b, control=control)
res.pvalue
array([0.62009281, 0.00582381])
P-значение, соответствующее сравнению между группой A и контрольной группой, превышает 0.05, поэтому мы не отвергаем нулевую гипотезу для этого сравнения. Однако p-значение, соответствующее сравнению между группой B и контрольной группой, меньше 0.05, поэтому мы рассматриваем экспериментальные результаты как свидетельство против нулевой гипотезы в пользу альтернативной: группа B имеет среднее значение, отличное от контрольной группы.