numpy.fft.fft#

fft.fft(a, n=None, ось=-1, norm=None, выход=None)[источник]#

Вычисляет одномерное дискретное преобразование Фурье.

Эта функция вычисляет одномерное n-точечное дискретное преобразование Фурье (ДПФ) с эффективным алгоритмом быстрого преобразования Фурье (БПФ) [CT].

Параметры:

aarray_like: Входной массив, может быть комплексным.
nint, необязательный: Длина преобразованной оси вывода. Если n меньше длины ввода, ввод обрезается. Если больше, ввод дополняется нулями. Если n не указана, длина ввода вдоль оси, заданной ось используется.
осьint, необязательный: Ось, по которой вычисляется БПФ. Если не указана, используется последняя ось.
norm{“backward”, “ortho”, “forward”}, опционально: Режим нормализации (см. numpy.fft). По умолчанию — «backward». Указывает, какое направление пары преобразований вперёд/назад масштабируется и с каким коэффициентом нормализации.

Новое в версии 1.20.0: Значения "backward", "forward" были добавлены.
выходcomplex ndarray, опционально: Если предоставлен, результат будет помещён в этот массив. Он должен быть соответствующей формы и dtype.

Новое в версии 2.0.0.

Возвращает:

выходкомплексный ndarray: Усечённый или дополненный нулями вход, преобразованный вдоль оси, указанной ось, или последний, если ось не указано.

Вызывает:

IndexError: Если ось не является допустимой осью для a.

Смотрите также

numpy.fft: для определения DFT и используемых соглашений.
ifft: Обратная величина fft.
fft2: Двумерное быстрое преобразование Фурье.
fftn: The n-мерное БПФ.
rfftn: The n-мерным БПФ реального входа.
fftfreq: Частотные бины для заданных параметров БПФ.

Примечания

БПФ (Быстрое Преобразование Фурье) относится к способу эффективного вычисления дискретного преобразования Фурье (ДПФ), используя симметрии в вычисляемых членах. Симметрия максимальна, когда n является степенью двойки, и преобразование поэтому наиболее эффективно для таких размеров.

ДПФ определяется, с соглашениями, используемыми в этой реализации, в документации для numpy.fft модуль.

Ссылки

[CT]

Кули, Джеймс У., и Джон У. Тьюки, 1965, "Алгоритм для машинного вычисления комплексных рядов Фурье," Math. Comput. 19: 297-301.

Примеры

>>> import numpy as np
>>> np.fft.fft(np.exp(2j * np.pi * np.arange(8) / 8))
array([-2.33486982e-16+1.14423775e-17j,  8.00000000e+00-1.25557246e-15j,
        2.33486982e-16+2.33486982e-16j,  0.00000000e+00+1.22464680e-16j,
       -1.14423775e-17+2.33486982e-16j,  0.00000000e+00+5.20784380e-16j,
        1.14423775e-17+1.14423775e-17j,  0.00000000e+00+1.22464680e-16j])

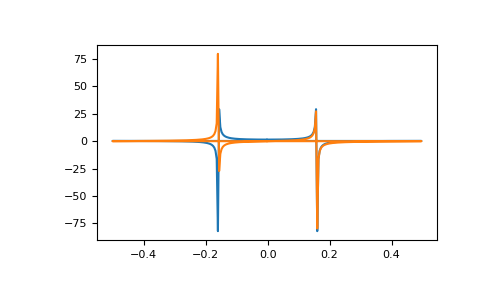
В этом примере действительный вход имеет БПФ, которое является эрмитовым, т.е. симметричным в действительной части и антисимметричным в мнимой части, как описано в numpy.fft : BUG: ограничить значение по умолчанию для get_num_build_jobs() до 8

>>> import matplotlib.pyplot as plt
>>> t = np.arange(256)
>>> sp = np.fft.fft(np.sin(t))
>>> freq = np.fft.fftfreq(t.shape[-1])
>>> _ = plt.plot(freq, sp.real, freq, sp.imag)
>>> plt.show()