Использование удобных классов#
Удобные классы, предоставляемые пакетом полиномов:
Name |
Предоставляет |
|---|---|
Степенные ряды |
|
Ряд Чебышёва |
|
Ряд Лежандра |
|
Ряд Лагерра |
|
Ряд Эрмита |
|
Ряд Эрмита-Эйлера |
Ряды в этом контексте — это конечные суммы соответствующих базисных функций полинома, умноженных на коэффициенты. Например, степенной ряд выглядит как
и имеет коэффициенты \([1, 2, 3]\). Ряд Чебышёва с теми же коэффициентами выглядит как
и в более общем случае
где в данном случае \(T_n\) являются функциями Чебышёва степени \(n\), но так же легко могут быть базисными функциями любого из других классов. Соглашение для всех классов заключается в том, что коэффициент \(c[i]\) соответствует базисной функции степени i.
Все классы являются неизменяемыми и имеют одинаковые методы, особенно они реализуют числовые операторы Python +, -, *, //, %, divmod, **, == и !=. Последние два могут быть немного проблематичными из-за ошибок округления с плавающей точкой. Теперь мы дадим краткую демонстрацию различных операций с использованием NumPy версии 1.7.0.
Основы#
Сначала нам нужен класс полинома и экземпляр полинома для работы. Классы можно импортировать непосредственно из пакета polynomial или из модуля соответствующего типа. Здесь мы импортируем из пакета и используем обычный класс Polynomial из-за его знакомости:
>>> from numpy.polynomial import Polynomial as P
>>> p = P([1,2,3])
>>> p
Polynomial([1., 2., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Обратите внимание, что в длинной версии вывода есть три части. Первая — коэффициенты, вторая — домен, а третья — окно:
>>> p.coef
array([1., 2., 3.])
>>> p.domain
array([-1., 1.])
>>> p.window
array([-1., 1.])
Вывод полинома отображает полиномиальное выражение в более привычном формате:
>>> print(p)
1.0 + 2.0·x + 3.0·x²
Обратите внимание, что строковое представление полиномов по умолчанию использует символы Юникода (кроме Windows) для выражения степеней и подстрочных индексов. Также доступно представление на основе ASCII (по умолчанию на Windows). Формат строки полинома можно переключить на уровне пакета с помощью
set_default_printstyle функция:
>>> np.polynomial.set_default_printstyle('ascii')
>>> print(p)
1.0 + 2.0 x + 3.0 x**2
или управляется для отдельных экземпляров полиномов с помощью форматирования строк:
>>> print(f"{p:unicode}")
1.0 + 2.0·x + 3.0·x²
Мы разберёмся с областью определения и окном, когда дойдём до подгонки, а пока мы игнорируем их и проходим через основные алгебраические и арифметические операции.
Сложение и вычитание:
>>> p + p
Polynomial([2., 4., 6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p - p
Polynomial([0.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Умножение:
>>> p * p
Polynomial([ 1., 4., 10., 12., 9.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Степени:
>>> p**2
Polynomial([ 1., 4., 10., 12., 9.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Деление:
Целочисленное деление, '//', является оператором деления для классов полиномов, полиномы рассматриваются как целые числа в этом отношении. Для версий Python < 3.x оператор '/' отображается на '//', как и для Python, для более поздних версий '/' будет работать только для деления на скаляры. В какой-то момент это будет устаревшим:
>>> p // P([-1, 1])
Polynomial([5., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Остаток:
>>> p % P([-1, 1])
Polynomial([6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Divmod:
>>> quo, rem = divmod(p, P([-1, 1]))
>>> quo
Polynomial([5., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> rem
Polynomial([6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Оценка:
>>> x = np.arange(5)
>>> p(x)
array([ 1., 6., 17., 34., 57.])
>>> x = np.arange(6).reshape(3,2)
>>> p(x)
array([[ 1., 6.],
[17., 34.],
[57., 86.]])
Замена:
Подставьте полином вместо x и раскройте результат. Здесь мы подставляем p в самого себя, что приводит к новому полиному степени 4 после раскрытия. Если рассматривать полиномы как функции, это композиция функций:
>>> p(p)
Polynomial([ 6., 16., 36., 36., 27.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Корни:
>>> p.roots()
array([-0.33333333-0.47140452j, -0.33333333+0.47140452j])
Не всегда удобно явно использовать экземпляры Polynomial, поэтому кортежи, списки, массивы и скаляры автоматически преобразуются в арифметических операциях:
>>> p + [1, 2, 3]
Polynomial([2., 4., 6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> [1, 2, 3] * p
Polynomial([ 1., 4., 10., 12., 9.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p / 2
Polynomial([0.5, 1. , 1.5], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Многочлены, различающиеся областью определения, окном или классом, нельзя смешивать в арифметических операциях:
>>> from numpy.polynomial import Chebyshev as T
>>> p + P([1], domain=[0,1])
Traceback (most recent call last):
File "" , line 1, in " , line 213, in __add__
TypeError: Domains differ
>>> p + P([1], window=[0,1])
Traceback (most recent call last):
File "" , line 1, in " , line 215, in __add__
TypeError: Windows differ
>>> p + T([1])
Traceback (most recent call last):
File "" , line 1, in " , line 211, in __add__
TypeError: Polynomial types differ
Но для подстановки могут использоваться разные типы. Фактически, именно так выполняется преобразование классов Polynomial между собой для приведения типа, области определения и окна:
>>> p(T([0, 1]))
Chebyshev([2.5, 2. , 1.5], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Что даёт полином p в форме Чебышёва. Это работает, потому что \(T_1(x) = x\) и подстановка \(x\) для \(x\) не изменяет исходный полином. Однако все умножения и деления будут выполняться с использованием рядов Чебышёва, следовательно, тип результата.
Предполагается, что все экземпляры полиномов неизменяемы, поэтому расширенные операции (+=, -=, и т.д.) и любой другой функционал, который нарушил бы неизменяемость экземпляра полинома, намеренно не реализованы.
Исчисление#
Экземпляры Polynomial могут быть интегрированы и дифференцированы.:
>>> from numpy.polynomial import Polynomial as P
>>> p = P([2, 6])
>>> p.integ()
Polynomial([0., 2., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p.integ(2)
Polynomial([0., 0., 1., 1.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Первый пример интегрирует p один раз, второй пример интегрирует его дважды. По умолчанию нижняя граница интегрирования и константа интегрирования равны 0, но обе могут быть указаны.:
>>> p.integ(lbnd=-1)
Polynomial([-1., 2., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p.integ(lbnd=-1, k=1)
Polynomial([0., 2., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
В первом случае нижняя граница интегрирования установлена в -1, а константа интегрирования равна 0. Во втором константа интегрирования установлена в 1. Дифференцирование проще, поскольку единственной опцией является количество раз, которое полином дифференцируется:
>>> p = P([1, 2, 3])
>>> p.deriv(1)
Polynomial([2., 6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p.deriv(2)
Polynomial([6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Другие конструкторы полиномов#
Конструирование полиномов путем указания коэффициентов — это лишь один способ получения экземпляра полинома; они также могут быть созданы путем указания их корней, преобразованием из других типов полиномов и методом наименьших квадратов. Подгонка обсуждается в отдельном разделе, другие методы демонстрируются ниже:
>>> from numpy.polynomial import Polynomial as P
>>> from numpy.polynomial import Chebyshev as T
>>> p = P.fromroots([1, 2, 3])
>>> p
Polynomial([-6., 11., -6., 1.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p.convert(kind=T)
Chebyshev([-9. , 11.75, -3. , 0.25], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Метод convert также может преобразовывать домен и окно:
>>> p.convert(kind=T, domain=[0, 1])
Chebyshev([-2.4375 , 2.96875, -0.5625 , 0.03125], domain=[0., 1.], window=[-1., 1.], symbol='x')
>>> p.convert(kind=P, domain=[0, 1])
Polynomial([-1.875, 2.875, -1.125, 0.125], domain=[0., 1.], window=[-1., 1.], symbol='x')
В версиях numpy >= 1.7.0 базис и преобразовать методы класса также доступны. Метод cast работает как метод convert, а метод basis возвращает базисный полином заданной степени:
>>> P.basis(3)
Polynomial([0., 0., 0., 1.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> T.cast(p)
Chebyshev([-9. , 11.75, -3. , 0.25], domain=[-1., 1.], window=[-1., 1.], symbol='x')
Преобразования между типами могут быть полезны, но это не рекомендуется для повседневного использования. Потеря численной точности при переходе от ряда Чебышева степени 50 к полиномиальному ряду той же степени может сделать результаты численного вычисления практически случайными.
Обучение#
Подгонка (fitting) — это причина, по которой область определения и window атрибуты являются частью удобных классов. Для иллюстрации проблемы значения полиномов Чебышёва до степени 5 показаны ниже.
>>> import matplotlib.pyplot as plt
>>> from numpy.polynomial import Chebyshev as T
>>> x = np.linspace(-1, 1, 100)
>>> for i in range(6):
... ax = plt.plot(x, T.basis(i)(x), lw=2, label=f"$T_{i}$")
...
>>> plt.legend(loc="upper left")
>>> plt.show()
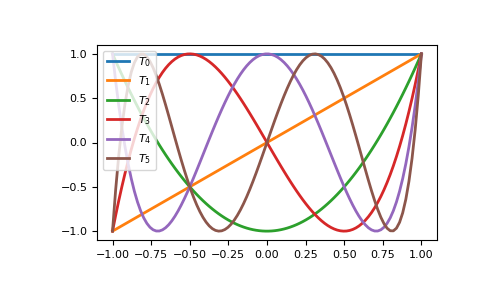
В диапазоне -1 <= x <= 1 они являются хорошими, равнопульсирующими функциями, лежащими между +/- 1. Те же графики в диапазоне -2 <= x <= 2 выглядят очень по-разному:
>>> import matplotlib.pyplot as plt
>>> from numpy.polynomial import Chebyshev as T
>>> x = np.linspace(-2, 2, 100)
>>> for i in range(6):
... ax = plt.plot(x, T.basis(i)(x), lw=2, label=f"$T_{i}$")
...
>>> plt.legend(loc="lower right")
>>> plt.show()
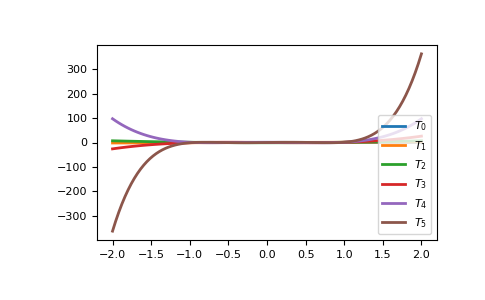
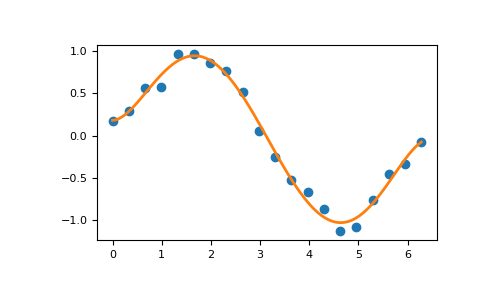
Как видно, «хорошие» части сократились до незначительности. При использовании полиномов Чебышёва для подгонки мы хотим использовать область, где x находится между -1 и 1, и это то, что window указывает. Однако маловероятно, что данные для подгонки имеют все свои точки данных в этом интервале, поэтому мы используем область определения чтобы указать интервал, в котором лежат точки данных. Когда выполняется подгонка, область сначала отображается на окно линейным преобразованием, и обычная аппроксимация методом наименьших квадратов выполняется с использованием отображённых точек данных. Окно и область подгонки являются частью возвращаемого ряда и автоматически используются при вычислении значений, производных и т.д. Если они не указаны в вызове, процедура подгонки будет использовать окно по умолчанию и наименьшую область, содержащую все точки данных. Это проиллюстрировано ниже для подгонки к зашумлённой синусоидальной кривой.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from numpy.polynomial import Chebyshev as T
>>> np.random.seed(11)
>>> x = np.linspace(0, 2*np.pi, 20)
>>> y = np.sin(x) + np.random.normal(scale=.1, size=x.shape)
>>> p = T.fit(x, y, 5)
>>> plt.plot(x, y, 'o')
>>> xx, yy = p.linspace()
>>> plt.plot(xx, yy, lw=2)
>>> p.domain
array([0. , 6.28318531])
>>> p.window
array([-1., 1.])
>>> plt.show()