Сглаживающие сплайны

Сглаживание сплайнами в 1D

Для задачи интерполяции задача состоит в построении кривой, проходящей через заданный набор точек данных. Это может быть неуместно, если данные зашумлены: тогда мы хотим построить гладкую кривую. \(g(x)\), который аппроксимирует входные данные без точного прохождения через каждую точку.

Для этой цели, scipy.interpolate позволяет конструировать сглаживающие сплайны которые определяют, насколько близка результирующая кривая, \(g(x)\), соответствует данным, и гладкость \(g(x)\). Математически задача состоит в решении регуляризованной задачи наименьших квадратов, где регуляризация контролирует гладкость \(g(x)\).

Мы предоставляем два подхода к построению сглаживающих сплайнов, которые различаются (1) формой штрафного члена и (2) базисом, в котором строится сглаживающая кривая. Ниже мы рассмотрим эти два подхода.

Первый вариант выполняется с помощью make_smoothing_spline функция, которая является чистой перереализацией классической gcvspl Пакет Fortran от H. Woltring. Последний вариант реализован make_splrep функция, которая является перереализацией библиотеки Fortran FITPACK от P. Dierckx. Устаревший интерфейс к библиотеке FITPACK также доступен.

"Классические" сглаживающие сплайны и критерий обобщённой перекрёстной проверки (GCV)

При заданных массивах данных x и y и массив неотрицательных веса, w, мы ищем кубическую сплайн-функцию g(x) который минимизирует

\[\sum\limits_{j=1}^n w_j \left\lvert y_j - g(x_j) \right\rvert^2 + \lambda\int\limits_{x_1}^{x_n} \left( g^{(2)}(u) \right)^2 d u\]

где \(\lambda \geqslant 0\) является неотрицательным параметром штрафа, и \(g^{(2)}(x)\) является второй производной от \(g(x)\). Суммирование в первом члене выполняется по точкам данных, \((x_j, y_j)\), а интеграл во втором члене берётся по всему интервалу \(x \in [x_1, x_n]\).

Здесь первый член штрафует отклонение сплайн-функции от данных, а второй член штрафует большие значения второй производной — что принимается как критерий гладкости кривой.

Целевая функция, \(g(x)\), принимается за естественный кубический сплайн с узлами в точках данных, \(x_j\), и минимизация проводится по коэффициентам сплайна при заданном значении \(\lambda\).

Очевидно, \(\lambda = 0\) соответствует задаче интерполяции — результат является естественный интерполяционный сплайн; в противоположном пределе, \(\lambda \gg 1\), результат \(g(x)\) приближается к прямой линии (поскольку минимизация эффективно обнуляет вторую производную от \(g(x)\)).

Функция сглаживания сильно зависит от \(\lambda\), и возможны несколько стратегий для выбора «оптимального» значения штрафа. Одна популярная стратегия — так называемый обобщённая кросс-валидация (GCV): концептуально это эквивалентно сравнению сплайн-функций, построенных на уменьшенных наборах данных, где мы исключаем одну точку данных. Прямое применение этой процедуры перекрёстной проверки с исключением по одному очень затратно, и мы используем более эффективный алгоритм GCV.

Для построения сглаживающего сплайна по данным и параметру штрафа мы используем функцию make_smoothing_spline. Его интерфейс похож на конструктор интерполяционных сплайнов, make_interp_spline: принимает массивы данных и возвращает вызываемый объект BSpline экземпляр.

Кроме того, он принимает необязательный lam аргумент keyword для указания параметра штрафа \(\lambda\). Если опущено или установлено в None, \(\lambda\) вычисляется через процедуру GCV.

Чтобы проиллюстрировать влияние параметра штрафа, рассмотрим простой пример синусоидальной кривой с некоторым шумом:

>>> import numpy as np
>>> from scipy.interpolate import make_smoothing_spline

Сгенерировать некоторые зашумленные данные:

>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y =  np.sin(x) + 0.4*rng.standard_normal(size=len(x))

Построить и отобразить сглаживающие сплайны для ряда значений параметра штрафа:

>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi
>>> for lam in [0, 0.02, 10, None]:
...     spl = make_smoothing_spline(x, y, lam=lam)
...     plt.plot(xnew, spl(xnew), '-.', label=fr'$\lambda=${lam}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()

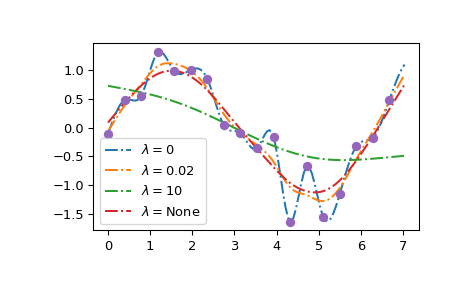
Мы ясно видим, что lam=0 строит интерполяционный сплайн; большие значения lam сглаживать результирующую кривую к прямой линии; и результат GCV, lam=None, близко к основной синусоидальной кривой.

Пакетная обработка y массивы

make_smoothing_spline конструктор принимает многомерные y массивы и необязательный axis параметр и интерпретирует их точно так же, как конструктор интерполирующего сплайна, make_interp_spline делает. Смотрите раздел интерполяции для обсуждения и примеров.

Сглаживающие сплайны с автоматическим выбором узлов

В дополнение к make_smoothing_spline, SciPy предоставляет альтернативу в виде make_splrep и make_splprep подпрограммы. Первая строит сплайн- функции, а вторая предназначена для параметрических сплайн-кривых в \(d > 1\) измерения.

Имея схожий API (получает массивы данных, возвращает BSpline экземпляр), они отличаются от make_smoothing_spline несколькими способами:

• функциональная форма штрафного члена отличается: эти процедуры используют скачки из \(k\)-я производная вместо интеграла от \((k-1)\)-я производная;

• вместо параметра штрафа \(\lambda\), параметр гладкости \(s\) используется;

• эти процедуры автоматически строят вектор узлов; в зависимости от входных данных, результирующие сплайны могут иметь гораздо меньше узлов, чем точек данных.

• по умолчанию граничные условия различаются: в то время как make_smoothing_spline строит натуральные кубические сплайны, эти процедуры по умолчанию используют граничные условия not-a-knot.

Рассмотрим алгоритм более подробно. Сначала, критерий сглаживания. Для заданной кубической сплайн-функции, \(g(x)\), определенный узлами, \(t_j\), и коэффициенты, \(c_j\), рассмотрите скачки третьей производной во внутренних узлах,

\[D_j = g^{(3)}(t_j + 0) - g^{(3)}(t_j - 0) .\]

(Для степени-\(k\) сплайнов, мы бы использовали скачки \(k\)-я производная.)

Если все \(D_j = 0\), затем \(g(x)\) является единым полиномом на всей области, охватываемой узлами. Таким образом, мы рассматриваем \(g(x)\) быть кусочно \(C^2\)-дифференцируемая сплайн-функция и использование в качестве критерия сглаживания суммы скачков,

\[\sum_j \left| D_j \right|^2 \to \mathrm{min} ,\]

где минимизация выполняется по коэффициентам сплайна и, возможно, по узлам сплайна.

Чтобы убедиться \(g(x)\) аппроксимирует входные данные, \(x_j\) и \(y_j\), мы вводим параметр гладкости \(s \geqslant 0\) и добавить ограничение, что

\[\sum_{j=1}^m \left[w_j \times \left(g(x_j) - y_j\right) \right]^2 \leqslant s .\]

В этой формулировке параметр гладкости \(s\) является пользовательским вводом, подобно параметру штрафа \(\lambda\) предназначен для классических сглаживающих сплайнов.

Обратите внимание, что предел s = 0 соответствует задаче интерполяции, где \(g(x_j) = y_j\). Увеличение s приводит к более гладким аппроксимациям, и в пределе при очень большом s, \(g(x)\) вырождается в единственный полином наилучшего приближения.

Для фиксированного вектора узлов и заданного значения \(s\), задача минимизации является линейной. Если мы также минимизируем относительно узлов, задача становится нелинейной. Таким образом, нам нужно указать итерационный процесс минимизации для построить вектор узлов вместе с коэффициентами сплайна.

Поэтому мы используем следующую процедуру:

• мы начинаем со сплайна без внутренних узлов и проверяем условие гладкости для предоставленного пользователем значения \(s\). Если оно выполняется, мы закончили. В противном случае,

• итерация, где на каждой итерации мы

  • добавить новые узлы, разделяя интервал с максимальным отклонением между сплайн-функцией \(g(x_j)\) и данные \(y_j\).

  • построить следующее приближение для \(g(x)\) и проверить критерий гладкости.

Итерации останавливаются, если либо выполняется условие гладкости, либо достигается максимально допустимое количество узлов. Последнее может быть либо задано пользователем, либо взято как значение по умолчанию len(x) + k + 1 что соответствует интерполяции массива данных x со сплайнами степени k.

Перефразируя и опуская детали, процедура заключается в итерации по векторам узлов, сгенерированным generate_knots, применяя make_lsq_spline на каждом шаге. В псевдокоде:

for t in generate_knots(x, y, s=s):
    g = make_lsq_spline(x, y, t=t)     # construct
    if ((y - g(x))**2).sum() < s:      # check smoothness
        break

Примечание

Для s=0, мы используем сокращение и строим интерполяционный сплайн с граничным условием not-a-knot вместо итераций.

Итеративная процедура построения вектора узлов доступна через функцию-генератор generate_knots. Для иллюстрации:

>>> import numpy as np
>>> from scipy.interpolate import generate_knots
>>> x = np.arange(7)
>>> y = x**4
>>> list(generate_knots(x, y, s=1))   # default is cubic splines, k=3
[array([0., 0., 0., 0., 6., 6., 6., 6.]),
 array([0., 0., 0., 0., 3., 6., 6., 6., 6.]),
 array([0., 0., 0., 0., 3., 5., 6., 6., 6., 6.]),
 array([0., 0., 0., 0., 2., 3., 4., 6., 6., 6., 6.])]

Для s=0, генератор прерывается:

>>> list(generate_knots(x, y, s=0))
[array([0, 0, 0, 0, 2, 3, 4, 6, 6, 6, 6])]

Примечание

В общем случае узлы размещаются в точках данных. Исключение составляют сплайны четного порядка, где узлы могут быть размещены вдали от данных. Это происходит, когда s=0 (интерполяция), или когда s достаточно мал, чтобы максимальное количество узлов было достигнуто, и процедура переключается на s=0 вектор узлов (иногда известный как абсциссы Гревилля).

>>> list(generate_knots(x, y, s=1, k=2))   # k=2, quadratic spline
[array([0., 0., 0., 6., 6., 6.]),
 array([0., 0., 0., 3., 6., 6., 6.]),
 array([0., 0., 0., 3., 5., 6., 6., 6.]),
 array([0., 0., 0., 2., 3., 5., 6., 6., 6.]),
 array([0. , 0. , 0. , 1.5, 2.5, 3.5, 4.5, 6. , 6. , 6. ])]   # Greville sites

Примечание

Эвристики для построения вектора узлов следуют алгоритму, используемому библиотекой FITPACK на Fortran. Алгоритм тот же, и небольшие различия возможны из-за округления с плавающей запятой.

Теперь мы проиллюстрируем make_splrep результаты, используя тот же игрушечный набор данных, что и в предыдущем разделе

>>> import numpy as np
>>> from scipy.interpolate import make_splrep

Сгенерируйте некоторые зашумленные данные

>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y =  np.sin(x) + 0.4*rng.standard_normal(size=len(x))

Построить и отобразить сглаживающие сплайны для ряда значений s параметр:

>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi

>>> plt.plot(xnew, np.sin(xnew), '-.', label='sin(x)')
>>> plt.plot(xnew, make_splrep(x, y, s=0)(xnew), '-', label='s=0')
>>> plt.plot(xnew, make_splrep(x, y, s=len(x))(xnew), '-', label=f's={len(x)}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()

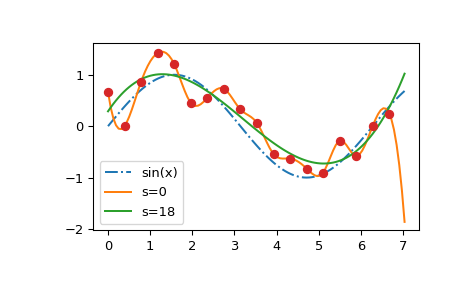
Мы видим, что \(s=0\) кривая следует за (случайными) флуктуациями точек данных, в то время как \(s > 0\) кривая близка к основной синусоидальной функции. Также обратите внимание, что экстраполированные значения сильно различаются в зависимости от значения \(s\).

Поиск хорошего значения \(s\) является процессом проб и ошибок. Если веса соответствуют обратным величинам стандартных отклонений входных данных, "хорошее" значение \(s\) ожидается где-то между \(m - \sqrt{2m}\) и \(m + \sqrt{2m}\), где \(m\) — это количество точек данных. Если все веса равны единице, разумным выбором может быть около \(s \sim m\,\sigma^2\), где \(\sigma\) является оценкой стандартного отклонения данных.

Примечание

Количество узлов сильно зависит от s. Возможно, что небольшие вариации s приводит к резким изменениям количества узлов.

Примечание

Оба make_smoothing_spline и make_splrep позволяют выполнять взвешенные подгонки, где пользователь предоставляет массив весов, w. Обратите внимание, что определение несколько отличается: make_smoothing_spline возводит веса в квадрат для согласованности с gcvspl, в то время как make_splrep не делает—для согласованности с FITPACK.

Сглаживающие сплайн-кривые в \(d>1\)

До сих пор мы рассматривали построение функций сглаживающих сплайнов, \(g(x)\) заданные массивы данных x и y. Теперь рассмотрим связанную проблему построения сглаживающего сплайна кривая, где мы рассматриваем данные как точки на плоскости, \(\mathbf{p}_j = (x_j, y_j)\), и мы хотим построить параметрическую функцию \(\mathbf{g}(\mathbf{p}) = (g_x(u), g_y(u))\), где значения параметра \(u_j\) соответствует \(x_j\) и \(y_j\).

Обратите внимание, что эта задача легко обобщается на более высокие размерности, \(d > 2\): мы просто имеем \(d\) массивы данных и построить параметрическую функцию с \(d\) компоненты.

Также обратите внимание, что выбор параметризации не может быть автоматизирован, и разные параметризации могут приводить к очень разным кривым для одних и тех же данных, даже для интерполирующие кривые.

После выбора конкретной формы параметризации задача построения сглаживающей кривой концептуально очень похожа на построение функции сглаживающего сплайна. Вкратце,

• узлы сплайна добавляются из значений параметра \(u\), и

• как минимизируемая функция стоимости, так и ограничение, которое мы рассматривали для сплайн-функции просто получает дополнительное суммирование по \(d\) компоненты.

«Параметрическое» обобщение make_splrep функция make_splprep, и его строка документации точно описывает математическую формулировку задачи минимизации, которую он решает.

Основное видимое пользователю различие параметрического случая — это пользовательский интерфейс:

• вместо двух массивов данных, x и y, make_splprep получает один двумерный массив, где второй размер имеет размер \(d\) и каждый массив данных хранится вдоль первого измерения (альтернативно, можно предоставить список одномерных массивов).

• возвращаемое значение - пара: a BSpline экземпляр и массив значений параметров, u, что соответствует входным массивам данных.

По умолчанию, make_splprep строит и возвращает параметризацию по длине хорды входных данных (см. Параметрические сплайн-кривые раздел для подробностей). В качестве альтернативы вы можете предоставить собственный массив значений параметров, u.

Для иллюстрации API рассмотрим простую задачу: у нас есть некоторые данные, взятые из фолиума Декарта плюс некоторый шум.

>>> import numpy as np
>>> from scipy.interpolate import make_splprep
>>> th = np.linspace(-0.2, np.pi/2 + 0.2, 21)
>>> r = 3 * np.sin(th) * np.cos(th) / (np.sin(th)**3 + np.cos(th)**3)
>>> x, y = r * np.cos(th), r * np.sin(th)

Добавьте немного шума и постройте интерполяторы

>>> rng = np.random.default_rng()
>>> xn = x + 0.1*rng.uniform(-1, 1, size=len(x))
>>> yn = y + 0.1*rng.uniform(-1, 1, size=len(x))
>>> spl, u = make_splprep([xn, yn], s=0)   # note the [xn, yn] argument
>>> spl_n, u_n = make_splprep([xn, yn], s=0.1)

И построить результаты (результат spl(u) является двумерным массивом, поэтому мы распаковываем его в пару x и y массивы для построения графиков).

>>> import matplotlib.pyplot as plt
>>> plt.plot(xn, yn, 'o')
>>> plt.plot(*spl(u), '--')
>>> plt.plot(*spl_n(u_n), '-')
>>> plt.show()

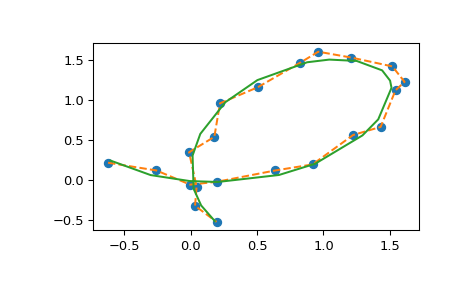
Пакетная обработка y массивы

В отличие от интерполирующие сплайны и Сглаживатели GCV, make_splrep и make_splprep делать не allow multidimensional y массивы и требуют, чтобы x.ndim == y.ndim == 1.

Техническая причина этого ограничения заключается в том, что длина вектора узлов t зависит от y значения, поэтому для пакетной y, пакетная t может быть рваным массивом, который BSpline не предназначен для обработки.

Поэтому если вам нужно обрабатывать пакетные входные данные, вам потребуется вручную перебирать пакет и создавать BSpline объект на срез пакета. После этого можно имитировать BSpline поведение для вычислений с обходным решением по аналогии с

class BatchSpline:
    """BSpline-like class with batch behavior."""
    def __init__(self, x, y, axis, *, spline, **kwargs):
        y = np.moveaxis(y, axis, -1)
        self._batch_shape = y.shape[:-1]
        self._splines = [
            spline(x, yi, **kwargs) for yi in y.reshape(-1, y.shape[-1])
        ]
        self._axis = axis

    def __call__(self, x):
        y = [spline(x) for spline in self._splines]
        y = np.reshape(y, self._batch_shape + x.shape)
        return np.moveaxis(y, -1, self._axis) if x.shape else y

Устаревшие процедуры для сглаживания сплайнами в 1-D

В дополнение к конструкторам сглаживающих сплайнов, которые мы обсуждали в предыдущих разделах, scipy.interpolate предоставляет прямые интерфейсы для подпрограмм из уважаемой библиотеки FITPACK на Fortran, созданной П. Дирксом.

Примечание

Эти интерфейсы следует считать устаревший—хотя мы не планируем их устаревание или удаление, мы рекомендуем, чтобы новый код использовал более современные альтернативы, make_smoothing_spline, make_splrep или make_splprep, вместо.

По историческим причинам, scipy.interpolate предоставляет два эквивалентных интерфейса для FITPACK: процедурный интерфейс и объектно-ориентированный интерфейс. Хотя они эквивалентны, эти интерфейсы имеют разные значения по умолчанию. Ниже мы рассмотрим их по очереди, начиная с процедурного интерфейса.

Процедурный (splrep)

Сплайн-интерполяция требует двух основных шагов: (1) вычисление сплайн-представления кривой и (2) вычисление сплайна в нужных точках. Чтобы найти сплайн-представление, существуют два разных способа представления кривой и получения коэффициентов (сглаживающего) сплайна: прямой и параметрический. Прямой метод находит сплайн-представление кривой в 2-D плоскости с помощью функции splrep. Первые два аргумента являются единственными обязательными, и они предоставляют \(x\) и \(y\) компоненты кривой. Нормальный вывод представляет собой кортеж из 3 элементов, \(\left(t,c,k\right)\) , содержащий точки узлов, \(t\) , коэффициенты \(c\) и порядок \(k\) сплайна. Порядок сплайна по умолчанию кубический, но это можно изменить с помощью входного ключевого слова, k.

Массив узлов определяет интервал интерполяции как t[k:-k], так что первый \(k+1\) и последний \(k+1\) элементы t определение массива граничные узлы. Коэффициенты представляют собой одномерный массив длиной не менее len(t) - k - 1. Некоторые процедуры дополняют этот массив, чтобы он имел len(c) == len(t)— эти дополнительные коэффициенты игнорируются при вычислении сплайна.

The tck-кортежный формат совместим с интерполяция B-сплайнами: вывод splrep может быть обёрнута в BSpline объекта, например. BSpline(*tck), и процедуры оценки/интегрирования/нахождения корней, описанные ниже, могут использовать tck-кортежи и BSpline объекты взаимозаменяемо.

Для кривых в N-мерном пространстве функция splprep позволяет определить кривую параметрически. Для этой функции требуется только 1 входной аргумент. Этот вход — список \(N\) массивы, представляющие кривую в N-мерном пространстве. Длина каждого массива — это количество точек кривой, и каждый массив предоставляет одну компоненту N-мерной точки данных. Параметр переменной задаётся с помощью ключевого аргумента, u, который по умолчанию представляет собой равномерно распределённую монотонную последовательность между \(0\) и \(1\) (т.е., равномерная параметризация).

Вывод состоит из двух объектов: кортежа из 3 элементов, \(\left(t,c,k\right)\) , содержащая сплайновое представление и переменную параметра \(u.\)

Коэффициенты представляют собой список \(N\) массивы, где каждый массив соответствует измерению входных данных. Обратите внимание, что узлы, t соответствуют параметризации кривой u.

Именованный аргумент, s используется для указания степени сглаживания при подгонке сплайна. Значение по умолчанию \(s\) является \(s=m-\sqrt{2m}\) где \(m\) это количество точек данных, которые подгоняются. Следовательно, если сглаживание не требуется, значение \(\mathbf{s}=0\) должны быть переданы в процедуры.

После того как сплайновая репрезентация данных определена, её можно оценить, используя splev функция или путем обертывания tck кортеж в BSpline объект, как показано ниже.

Мы начинаем с иллюстрации эффекта s параметр при сглаживании некоторых синтетических зашумленных данных

>>> import numpy as np
>>> from scipy.interpolate import splrep, BSpline

Сгенерируйте некоторые зашумленные данные

>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y =  np.sin(x) + 0.4*rng.standard_normal(size=len(x))

Построить два сплайна с разными значениями s.

>>> tck = splrep(x, y, s=0)
>>> tck_s = splrep(x, y, s=len(x))

И построить их

>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi
>>> plt.plot(xnew, np.sin(xnew), '-.', label='sin(x)')
>>> plt.plot(xnew, BSpline(*tck)(xnew), '-', label='s=0')
>>> plt.plot(xnew, BSpline(*tck_s)(xnew), '-', label=f's={len(x)}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()

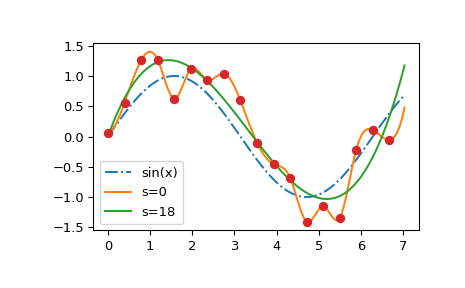
Мы видим, что s=0 кривая следует за (случайными) флуктуациями точек данных, в то время как s > 0 кривая близка к базовой синусоидальной функции. Также обратите внимание, что экстраполированные значения сильно различаются в зависимости от значения s.

Значение по умолчанию для s зависит от того, предоставлены ли веса или нет, а также отличается для splrep и splprep. Поэтому мы рекомендуем всегда предоставлять значение s явно.

Манипулирование сплайн-объектами: процедурный (splXXX)

После определения сплайн-представления данных, доступны функции для вычисления сплайна (splev) и её производные (splev, spalde) в любой точке и интеграл сплайна между любыми двумя точками ( splint). Кроме того, для кубических сплайнов ( \(k=3\) ) с 8 или более узлами, корни сплайна можно оценить ( sproot). Эти функции демонстрируются в следующем примере.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import interpolate

Кубический сплайн

>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
>>> y = np.sin(x)
>>> tck = interpolate.splrep(x, y, s=0)
>>> xnew = np.arange(0, 2*np.pi, np.pi/50)
>>> ynew = interpolate.splev(xnew, tck, der=0)

Обратите внимание, что последняя строка эквивалентна BSpline(*tck)(xnew).

>>> plt.figure()
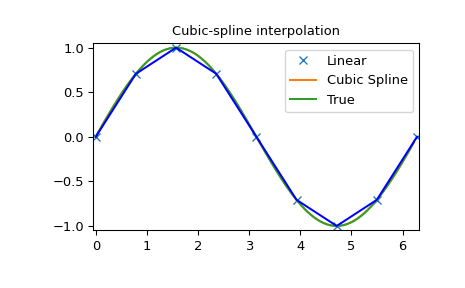
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Cubic-spline interpolation')
>>> plt.show()

Производная сплайна

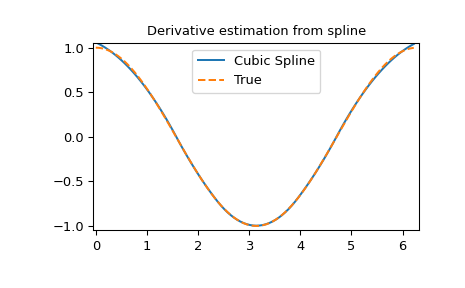
>>> yder = interpolate.splev(xnew, tck, der=1)   # or BSpline(*tck)(xnew, 1)
>>> plt.figure()
>>> plt.plot(xnew, yder, xnew, np.cos(xnew),'--')
>>> plt.legend(['Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Derivative estimation from spline')
>>> plt.show()

Все производные сплайна

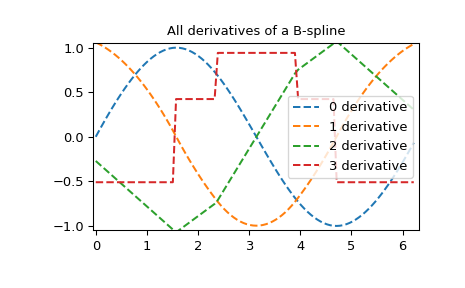
>>> yders = interpolate.spalde(xnew, tck)
>>> plt.figure()
>>> for i in range(len(yders[0])):
...    plt.plot(xnew, [d[i] for d in yders], '--', label=f"{i} derivative")
>>> plt.legend()
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('All derivatives of a B-spline')
>>> plt.show()

Интеграл сплайна

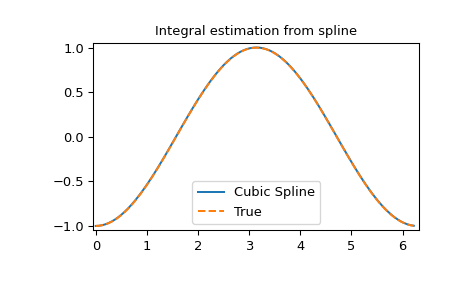
>>> def integ(x, tck, constant=-1):
...     x = np.atleast_1d(x)
...     out = np.zeros(x.shape, dtype=x.dtype)
...     for n in range(len(out)):
...         out[n] = interpolate.splint(0, x[n], tck)
...     out += constant
...     return out

>>> yint = integ(xnew, tck)
>>> plt.figure()
>>> plt.plot(xnew, yint, xnew, -np.cos(xnew), '--')
>>> plt.legend(['Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Integral estimation from spline')
>>> plt.show()

Корни сплайна

>>> interpolate.sproot(tck)
array([3.1416])  # may vary

Обратите внимание, что sproot может не найти очевидного решения на границе интервала аппроксимации, \(x = 0\). Если определить сплайн на немного большем интервале, мы восстановим оба корня \(x = 0\) и \(x = \pi\):

>>> x = np.linspace(-np.pi/4, np.pi + np.pi/4, 51)
>>> y = np.sin(x)
>>> tck = interpolate.splrep(x, y, s=0)
>>> interpolate.sproot(tck)
array([0., 3.1416])

Параметрический сплайн

>>> t = np.arange(0, 1.1, .1)
>>> x = np.sin(2*np.pi*t)
>>> y = np.cos(2*np.pi*t)
>>> tck, u = interpolate.splprep([x, y], s=0)
>>> unew = np.arange(0, 1.01, 0.01)
>>> out = interpolate.splev(unew, tck)
>>> plt.figure()
>>> plt.plot(x, y, 'x', out[0], out[1], np.sin(2*np.pi*unew), np.cos(2*np.pi*unew), x, y, 'b')
>>> plt.legend(['Linear', 'Cubic Spline', 'True'])
>>> plt.axis([-1.05, 1.05, -1.05, 1.05])
>>> plt.title('Spline of parametrically-defined curve')
>>> plt.show()

Обратите внимание, что в последнем примере, splprep возвращает коэффициенты сплайна в виде списка массивов, где каждый массив соответствует измерению входных данных. Таким образом, чтобы обернуть его вывод в BSpline, нам нужно транспонировать коэффициенты (или использовать BSpline(..., axis=1)):

>>> tt, cc, k = tck
>>> cc = np.array(cc)
>>> bspl = BSpline(tt, cc.T, k)    # note the transpose
>>> xy = bspl(u)
>>> xx, yy = xy.T   # transpose to unpack into a pair of arrays
>>> np.allclose(x, xx)
True
>>> np.allclose(y, yy)
True

Объектно-ориентированный (UnivariateSpline)

Возможности аппроксимации сплайнами, описанные выше, также доступны через объектно-ориентированный интерфейс. 1-D сплайны являются объектами класса UnivariateSpline класс, и создаются с помощью \(x\) и \(y\) компоненты кривой, предоставленные в качестве аргументов конструктору. Класс определяет __call__, позволяя объекту вызываться со значениями оси x, в которых сплайн должен быть оценен, возвращая интерполированные значения y. Это показано в примере ниже для подкласса InterpolatedUnivariateSpline. integral, derivatives, и roots методы также доступны в UnivariateSpline объекты, позволяющие вычислять определённые интегралы, производные и корни для сплайна.

Класс UnivariateSpline также может использоваться для сглаживания данных путём задания ненулевого значения параметра сглаживания s, с тем же значением, что и s ключевое слово splrep функция описанная выше. Это приводит к сплайну, который имеет меньше узлов, чем количество точек данных, и, следовательно, больше не является строго интерполирующим сплайном, а скорее сглаживающим сплайном. Если это нежелательно, то InterpolatedUnivariateSpline класс доступен. Это подкласс UnivariateSpline которая всегда проходит через все точки (эквивалентно принудительному установлению параметра сглаживания в 0). Этот класс демонстрируется в примере ниже.

The LSQUnivariateSpline класс является другим подклассом UnivariateSpline. Он позволяет пользователю явно указать количество и расположение внутренних узлов с параметром t. Это позволяет создавать настраиваемые сплайны с нелинейным шагом, интерполировать в одних областях и сглаживать в других, или изменять характер сплайна.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import interpolate

InterpolatedUnivariateSpline

>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
>>> y = np.sin(x)
>>> s = interpolate.InterpolatedUnivariateSpline(x, y)
>>> xnew = np.arange(0, 2*np.pi, np.pi/50)
>>> ynew = s(xnew)

>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'InterpolatedUnivariateSpline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('InterpolatedUnivariateSpline')
>>> plt.show()

LSQUnivarateSpline с неравномерными узлами

>>> t = [np.pi/2-.1, np.pi/2+.1, 3*np.pi/2-.1, 3*np.pi/2+.1]
>>> s = interpolate.LSQUnivariateSpline(x, y, t, k=2)
>>> ynew = s(xnew)

>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'LSQUnivariateSpline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Spline with Specified Interior Knots')
>>> plt.show()

2-D сглаживающие сплайны

В дополнение к сглаживанию 1-D сплайнов, библиотека FITPACK предоставляет средства для аппроксимации 2-D поверхности к двумерным данным. Поверхности можно рассматривать как функции двух аргументов, \(z = g(x, y)\), построенные как тензорные произведения одномерных сплайнов.

Предполагая, что данные хранятся в трех массивах, x, y и z, существует два способа интерпретации этих массивов данных. Первый — разбросанные задача интерполяции — данные предполагаются парными, т.е. пары значений x[i] и y[i] представляют координаты точки i, что соответствует z[i].

Поверхность \(g(x, y)\) сконструирована для удовлетворения

\[\sum_i \left[ w_i (g(x_i, y_i) - z_i)\right]^2 \leqslant s\]

где \(w_i\) являются неотрицательными весами, и s является входным параметром, известным как коэффициент сглаживания, который контролирует взаимодействие между гладкостью результирующей функции g(x, y) и качество аппроксимации данных (т.е., различия между \(g(x_i, y_i)\) и \(z_i\)). Предел \(s = 0\) формально соответствует интерполяции, где поверхность проходит через входные данные, \(g(x_i, y_i) = z_i\). Однако см. примечание ниже.

Второй случай — прямоугольная сетка интерполяционная задача — где точки данных предполагаются находящимися на прямоугольной сетке, определённой всеми парами элементов x и y массивы. Для этой задачи, z массив предполагается двумерным, и z[i, j] соответствует (x[i], y[j]). Бивариативная сплайн-функция \(g(x, y)\) сконструирована для удовлетворения

\[\sum_i \sum_j \left[ (g(x_i, y_j) - z_{i,j})\right]^2 \leqslant s\]

где s является коэффициентом сглаживания. Здесь предел \(s=0\) также формально соответствует интерполяции, \(g(x_i, y_j) = z_{i, j}\).

Примечание

Внутренне, сглаживающая поверхность \(g(x, y)\) строится путем размещения узлов сплайна в ограничивающем прямоугольнике, определенном массивами данных. Узлы размещаются автоматически с помощью алгоритма FITPACK до достижения желаемой гладкости.

Узлы могут быть размещены вдали от точек данных.

В то время как \(s=0\) формально соответствует бивариантной сплайн-интерполяции, алгоритм FITPACK не предназначен для интерполяции и может привести к неожиданным результатам.

(lu,piv,b,[trans,overwrite_b]) griddata; для данных на регулярной сетке предпочтительнее RegularGridInterpolator.

Примечание

Если входные данные, x и y, таков, что входные размерности имеют несоизмеримые единицы и различаются на много порядков величины, интерполянт \(g(x, y)\) может иметь численные артефакты. Рекомендуется масштабировать данные перед интерполяцией.

Теперь рассмотрим две задачи аппроксимации сплайнами по очереди.

Бивариативная сплайн-аппроксимация разбросанных данных

Существует два интерфейса для базовой библиотеки FITPACK: процедурный и объектно-ориентированный.

Процедурный интерфейс (`bisplrep`)

Для (гладкой) аппроксимации сплайнами 2-D поверхности функция bisplrep доступна. Эта функция принимает в качестве обязательных входных данных Одномерный массивы x, y, и z, которые представляют точки на поверхности \(z=f(x, y).\) Порядки сплайна в x и y направления могут быть указаны через необязательные параметры kx и ky. По умолчанию используется бикубический сплайн, kx=ky=3.

Вывод bisplrep является списком [tx ,ty, c, kx, ky] , записи которого представляют соответственно компоненты позиций узлов, коэффициенты сплайна и порядок сплайна в каждой координате. Удобно хранить этот список в одном объекте, tck, чтобы его можно было легко передать в функцию bisplev. Ключевое слово, s , может использоваться для изменения степени сглаживания, применяемого к данным при определении подходящего сплайна. Рекомендуемые значения для \(s\) зависят от весов \(w_i\). Если они взяты как \(1/d_i\), с \(d_i\) оценка стандартного отклонения \(z_i\), хорошее значение \(s\) должен быть найден в диапазоне \(m- \sqrt{2m}, m + \sqrt{2m}\), где где \(m\) — это количество точек данных в x, y, и z векторы.

Значение по умолчанию: \(s=m-\sqrt{2m}\). В результате, если сглаживание не требуется, то в `bisplrep` следует передать ``s=0``. (Однако см. примечание выше).

Для вычисления 2-D сплайна и его частных производных (до порядка сплайна), функция bisplev требуется. Эта функция принимает в качестве первых двух аргументов два 1-D массива чье векторное произведение задаёт область, по которой вычисляется сплайн. Третий аргумент — это tck список, возвращённый из bisplrep. При необходимости, четвёртый и пятый аргументы задают порядки частной производной в \(x\) и \(y\) направление, соответственно.

Примечание

Важно отметить, что 2-D интерполяция не должна использоваться для нахождения сплайн-представления изображений. Используемый алгоритм не подходит для большого количества входных точек. scipy.signal и scipy.ndimage содержат более подходящие алгоритмы для нахождения сплайн-представления изображения.

Команды 2-D интерполяции предназначены для использования при интерполяции 2-D функции, как показано в следующем примере. Этот пример использует mgrid команда в NumPy, которая полезна для определения «сетки» во многих измерениях. (См. также ogrid команда, если полная сетка не нужна). Количество выходных аргументов и количество измерений каждого аргумента определяется количеством объектов индексации, переданных в mgrid.

>>> import numpy as np
>>> from scipy import interpolate
>>> import matplotlib.pyplot as plt

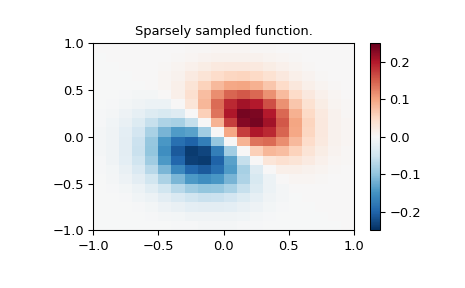
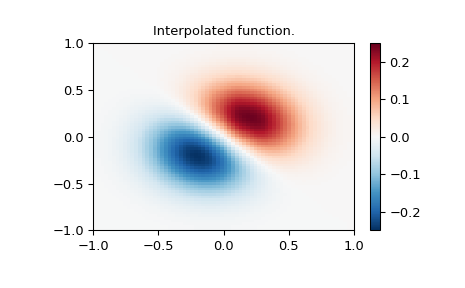
Определить функцию на разрежённой сетке 20x20

>>> x_edges, y_edges = np.mgrid[-1:1:21j, -1:1:21j]
>>> x = x_edges[:-1, :-1] + np.diff(x_edges[:2, 0])[0] / 2.
>>> y = y_edges[:-1, :-1] + np.diff(y_edges[0, :2])[0] / 2.
>>> z = (x+y) * np.exp(-6.0*(x*x+y*y))

>>> plt.figure()
>>> lims = dict(cmap='RdBu_r', vmin=-0.25, vmax=0.25)
>>> plt.pcolormesh(x_edges, y_edges, z, shading='flat', **lims)
>>> plt.colorbar()
>>> plt.title("Sparsely sampled function.")
>>> plt.show()

Интерполировать функцию на новой сетке 70x70

>>> xnew_edges, ynew_edges = np.mgrid[-1:1:71j, -1:1:71j]
>>> xnew = xnew_edges[:-1, :-1] + np.diff(xnew_edges[:2, 0])[0] / 2.
>>> ynew = ynew_edges[:-1, :-1] + np.diff(ynew_edges[0, :2])[0] / 2.
>>> tck = interpolate.bisplrep(x, y, z, s=0)
>>> znew = interpolate.bisplev(xnew[:,0], ynew[0,:], tck)

>>> plt.figure()
>>> plt.pcolormesh(xnew_edges, ynew_edges, znew, shading='flat', **lims)
>>> plt.colorbar()
>>> plt.title("Interpolated function.")
>>> plt.show()

Объектно-ориентированный интерфейс (`SmoothBivariateSpline`)

Объектно-ориентированный интерфейс для сглаживания двумерных сплайнов разбросанных данных, SmoothBivariateSpline класс, реализует подмножество функциональности bisplrep / bisplev пара, и имеет разные значения по умолчанию.

Он принимает элементы массива весов равными единице, \(w_i = 1\) и автоматически строит векторы узлов с учетом входного значения коэффициента сглаживания s— значение по умолчанию: \(m\), количество точек данных.

Порядки сплайнов в x и y направления управляются необязательными параметрами kx и ky, со значением по умолчанию kx=ky=3.

Мы демонстрируем эффект коэффициента сглаживания на следующем примере:

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import SmoothBivariateSpline

import warnings
warnings.simplefilter('ignore')

train_x, train_y = np.meshgrid(np.arange(-5, 5, 0.5), np.arange(-5, 5, 0.5))
train_x = train_x.flatten()
train_y = train_y.flatten()

def z_func(x, y):
    return np.cos(x) + np.sin(y) ** 2 + 0.05 * x + 0.1 * y

train_z = z_func(train_x, train_y)
interp_func = SmoothBivariateSpline(train_x, train_y, train_z, s=0.0)
smth_func = SmoothBivariateSpline(train_x, train_y, train_z)

test_x = np.arange(-9, 9, 0.01)
test_y = np.arange(-9, 9, 0.01)
grid_x, grid_y = np.meshgrid(test_x, test_y)

interp_result = interp_func(test_x, test_y).T
smth_result = smth_func(test_x, test_y).T
perfect_result = z_func(grid_x, grid_y)

fig, axes = plt.subplots(1, 3, figsize=(16, 8))
extent = [test_x[0], test_x[-1], test_y[0], test_y[-1]]
opts = dict(aspect='equal', cmap='nipy_spectral', extent=extent, vmin=-1.5, vmax=2.5)

im = axes[0].imshow(perfect_result, **opts)
fig.colorbar(im, ax=axes[0], orientation='horizontal')
axes[0].plot(train_x, train_y, 'w.')
axes[0].set_title('Perfect result, sampled function', fontsize=21)

im = axes[1].imshow(smth_result, **opts)
axes[1].plot(train_x, train_y, 'w.')
fig.colorbar(im, ax=axes[1], orientation='horizontal')
axes[1].set_title('s=default', fontsize=21)

im = axes[2].imshow(interp_result, **opts)
fig.colorbar(im, ax=axes[2], orientation='horizontal')
axes[2].plot(train_x, train_y, 'w.')
axes[2].set_title('s=0', fontsize=21)

plt.tight_layout()
plt.show()

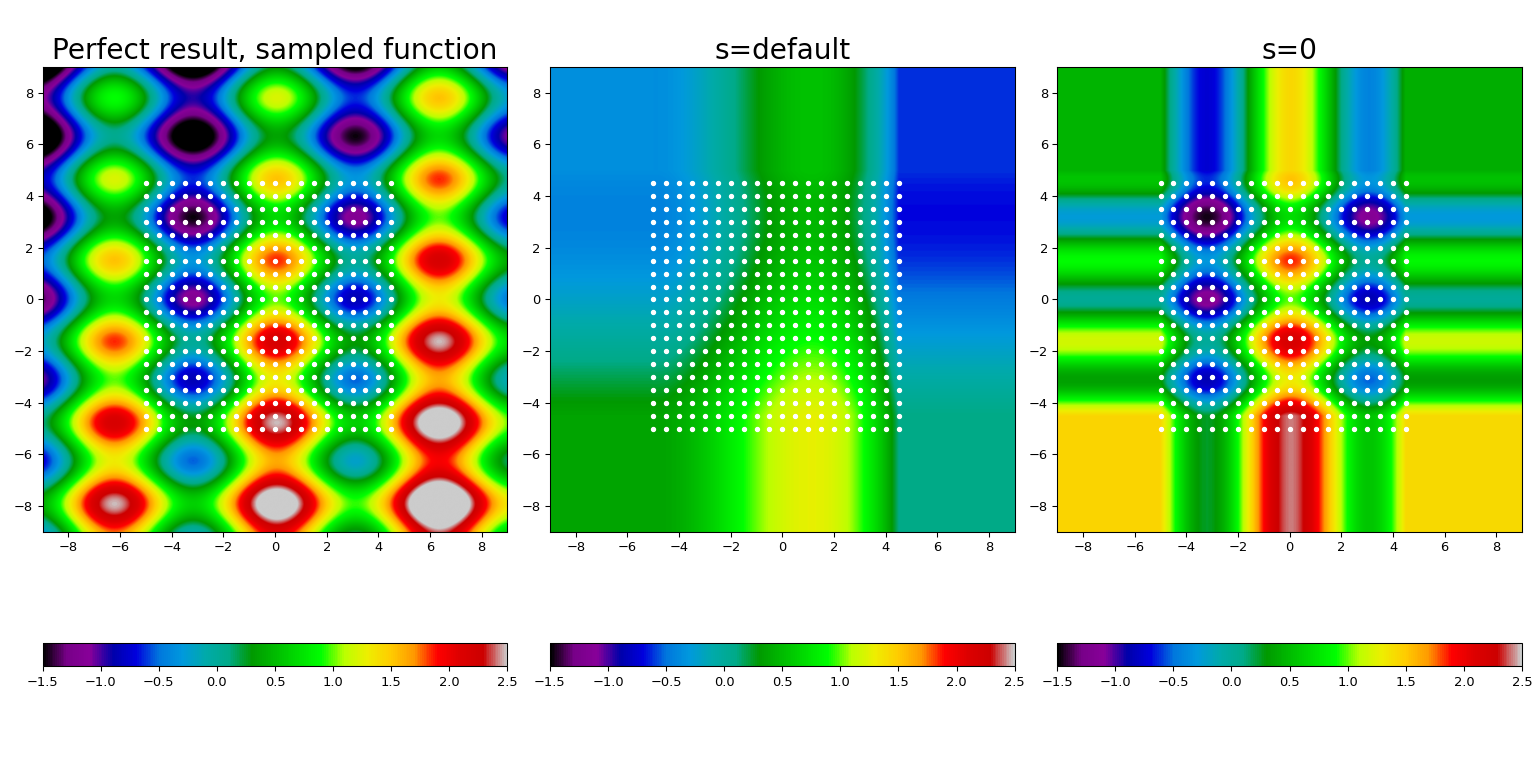
Здесь мы берем известную функцию (показана на левой панели), берем ее выборку на сетке точек (показаны белыми точками) и строим сплайн-аппроксимацию, используя сглаживание по умолчанию (центральная панель) и принудительную интерполяцию (правая панель).

Несколько особенностей хорошо видны. Во-первых, значение по умолчанию для s обеспечивает слишком сильное сглаживание для этих данных; принудительное выполнение условия интерполяции, s = 0, позволяет восстановить исходную функцию с разумной точностью. Во-вторых, вне диапазона интерполяции (т.е. области, покрытой белыми точками) результат экстраполируется с использованием константы ближайшего соседа. Наконец, нам пришлось заглушить предупреждения (что, да, плохой стиль!).

Предупреждение здесь выдается в s=0 случай и сигнализирует о внутренней сложности, с которой FITPACK столкнулся при принудительном выполнении условия интерполяции. Если вы видите это предупреждение в своём коде, рассмотрите переход на bisplrep и увеличить его nxest, nyest параметры (см. bisplrep docstring для подробностей).

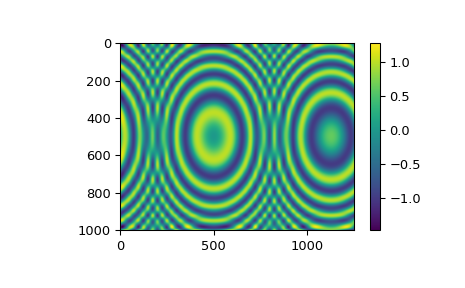
Бивариативная сплайн-аппроксимация данных на сетке

Для сеточных 2D данных подгонка сглаживающего тензорного произведения сплайнов может быть выполнена с использованием RectBivariateSpline класс. Он имеет интерфейс, похожий на интерфейс SmoothBivariateSpline, основное отличие в том, что одномерные входные массивы x и y понимаются как определяющие 2D сетку (как их внешнее произведение), и z массив является двумерным с формой len(x) by len(y).

Порядки сплайнов в x и y направления управляются необязательными параметрами kx и ky, со значением по умолчанию kx=ky=3, т.е. бикубический сплайн.

Значение по умолчанию для коэффициента сглаживания — s=0. Тем не менее, мы рекомендуем всегда указывать s явно.

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import RectBivariateSpline

x = np.arange(-5.01, 5.01, 0.25)        # the grid is an outer product
y = np.arange(-5.01, 7.51, 0.25)        # of x and y arrays

xx, yy = np.meshgrid(x, y, indexing='ij')
z = np.sin(xx**2 + 2.*yy**2)            # z array needs to be 2-D

func = RectBivariateSpline(x, y, z, s=0)

xnew = np.arange(-5.01, 5.01, 1e-2)
ynew = np.arange(-5.01, 7.51, 1e-2)
znew = func(xnew, ynew)

plt.imshow(znew)
plt.colorbar()
plt.show()

Бивариативная сплайн-аппроксимация данных в сферических координатах

Если ваши данные заданы в сферических координатах, \(r = r(\theta, \phi)\), SmoothSphereBivariateSpline и RectSphereBivariateSpline предоставляют удобные аналоги SmoothBivariateSpline и RectBivariateSpline, соответственно.

Эти классы обеспечивают периодичность сплайн-аппроксимаций для \(\theta \in [0, \pi]\) и \(\phi \in [0, 2\pi]\)и предоставляют некоторый контроль над непрерывностью на полюсах. Подробности см. в строках документации этих классов.