interp2d руководство по переходу

Эта страница содержит три набора демонстраций:

• низкоуровневые замены FITPACK для scipy.interpolate.interp2d для обратно совместимой с ошибками scipy.interpolate.interp2d замены;

• рекомендуемые замены для scipy.interpolate.interp2d для использования в новом коде;

• демонстрация режимов сбоя 2D линейной интерполяции на основе FITPACK и рекомендуемые замены.

1. Как перейти от использования interp2d

interp2d бесшумно переключается между интерполяцией на регулярной 2D сетке и интерполяцией 2D разбросанных данных. Переключение основано на длинах (развёрнутых) x, y, и z массивы. Короче говоря, для регулярной сетки используйте scipy.interpolate.RectBivariateSpline; для разбросанной интерполяции используйте bisprep/bisplev комбинация. Ниже приведены примеры буквального перехода точка-за-точку, который должен сохранить interp2d результаты точно.

1.1 interp2d на регулярной сетке

Мы начинаем с (слегка изменённого) примера из документации.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import interp2d, RectBivariateSpline

>>> x = np.arange(-5.01, 5.01, 0.25)
>>> y = np.arange(-5.01, 7.51, 0.25)
>>> xx, yy = np.meshgrid(x, y)
>>> z = np.sin(xx**2 + 2.*yy**2)
>>> f = interp2d(x, y, z, kind='cubic')

Это путь кода «регулярной сетки», потому что

>>> z.size == len(x) * len(y)
True

Также обратите внимание, что x.size != y.size:

>>> x.size, y.size
(41, 51)

Теперь создадим удобную функцию для построения интерполятора и его отрисовки.

>>> def plot(f, xnew, ynew):
...    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
...    znew = f(xnew, ynew)
...    ax1.plot(x, z[0, :], 'ro-', xnew, znew[0, :], 'b-')
...    im = ax2.imshow(znew)
...    plt.colorbar(im, ax=ax2)
...    plt.show()
...    return znew
...
>>> xnew = np.arange(-5.01, 5.01, 1e-2)
>>> ynew = np.arange(-5.01, 7.51, 1e-2)
>>> znew_i = plot(f, xnew, ynew)

Замена: Используйте RectBivariateSpline, результат идентичен

Обратите внимание на транспонирование: сначала в конструкторе, затем вам нужно транспонировать результат вычисления. Это делается для отмены транспонирования interp2d делает.

>>> r = RectBivariateSpline(x, y, z.T)
>>> rt = lambda xnew, ynew: r(xnew, ynew).T
>>> znew_r = plot(rt, xnew, ynew)

>>> from numpy.testing import assert_allclose
>>> assert_allclose(znew_i, znew_r, atol=1e-14)

Порядок интерполяции: линейный, кубический и т.д.

interp2d по умолчанию kind="linear", который является линейным в обоих направлениях, x- и y-. RectBivariateSpline, с другой стороны, по умолчанию использует кубическую интерполяцию, kx=3, ky=3.

Вот точное соответствие:

interp2d	RectBivariateSpline
без kwargs	kx = 1, ky = 1
kind='linear'	kx = 1, ky = 1
kind='cubic'	kx = 3, ky = 3

1.2. interp2d с полными координатами точек (интерполяция разбросанных данных)

Здесь мы сглаживаем сетку из предыдущего упражнения, чтобы проиллюстрировать функциональность.

>>> xxr = xx.ravel()
>>> yyr = yy.ravel()
>>> zzr = z.ravel()
>>> f = interp2d(xxr, yyr, zzr, kind='cubic')

Обратите внимание, что это путь кода «нерегулярной сетки», предназначенный для разбросанных данных, с len(x) == len(y) == len(z).

>>> len(xxr) == len(yyr) == len(zzr)
True

>>> xnew = np.arange(-5.01, 5.01, 1e-2)
>>> ynew = np.arange(-5.01, 7.51, 1e-2)
>>> znew_i = plot(f, xnew, ynew)

Замена: Используйте scipy.interpolate.bisplrep / scipy.interpolate.bisplev напрямую

>>> from scipy.interpolate import bisplrep, bisplev
>>> tck = bisplrep(xxr, yyr, zzr, kx=3, ky=3, s=0)
# convenience: make up a callable from bisplev
>>> ff = lambda xnew, ynew: bisplev(xnew, ynew, tck).T   # Note the transpose, to mimic what interp2d does
>>> znew_b = plot(ff, xnew, ynew)

>>> assert_allclose(znew_i, znew_b, atol=1e-15)

Порядок интерполяции: линейный, кубический и т.д.

interp2d по умолчанию kind="linear", который является линейным в обоих направлениях, x- и y-. bisplrep, с другой стороны, по умолчанию использует кубическую интерполяцию, kx=3, ky=3.

Вот точное соответствие:

interp2d	bisplrep
без kwargs	kx = 1, ky = 1
kind='linear'	kx = 1, ky = 1
kind='cubic'	kx = 3, ky = 3

2. Альтернатива interp2d: регулярная сетка

Для нового кода рекомендуется альтернатива RegularGridInterpolator. Это независимая реализация, не основанная на FITPACK. Поддерживает ближайшую, линейную интерполяцию и сплайны-произведения тензоров нечётного порядка.

Узлы сплайна гарантированно совпадают с точками данных.

Обратите внимание, что здесь:

1. аргумент кортежа, это (x, y)

2. z массив нуждается в транспонировании

3. ключевое слово называется метод, а не kind

4. bounds_error аргумент является True по умолчанию.

>>> from scipy.interpolate import RegularGridInterpolator as RGI
>>> r = RGI((x, y), z.T, method='linear', bounds_error=False)

Оценка: создание 2D сетки. Использование indexing='ij' и sparse=True чтобы сэкономить память:

>>> xxnew, yynew = np.meshgrid(xnew, ynew, indexing='ij', sparse=True)

Вычислить, обратите внимание на аргумент кортежа:

>>> znew_reggrid = r((xxnew, yynew))

>>> fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
# Again, note the transpose to undo the `interp2d` convention
>>> znew_reggrid_t = znew_reggrid.T
>>> ax1.plot(x, z[0, :], 'ro-', xnew, znew_reggrid_t[0, :], 'b-')
>>> im = ax2.imshow(znew_reggrid_t)
>>> plt.colorbar(im, ax=ax2)

3. Разреженная 2D линейная интерполяция: предпочитать LinearNDInterpolator to SmoothBivariateSpline или bisplrep

Для 2D линейной интерполяции разбросанных данных, оба SmoothBivariateSpline и biplrep может либо выдавать предупреждения, либо не интерполировать данные, либо создавать сплайны с узлами вне точек данных. Вместо этого предпочтительнее LinearNDInterpolator, который основан на триангуляции данных через QHull.

# TestSmoothBivariateSpline::test_integral
>>> from scipy.interpolate import SmoothBivariateSpline, LinearNDInterpolator
>>> x = np.array([1,1,1,2,2,2,4,4,4])
>>> y = np.array([1,2,3,1,2,3,1,2,3])
>>> z = np.array([0,7,8,3,4,7,1,3,4])

Теперь используйте линейную интерполяцию по триангуляции данных на основе Qhull:

>>> xy = np.c_[x, y]   # or just list(zip(x, y))
>>> lut2 = LinearNDInterpolator(xy, z)
>>> X = np.linspace(min(x), max(x))
>>> Y = np.linspace(min(y), max(y))
>>> X, Y = np.meshgrid(X, Y)

Результат легко понять и интерпретировать:

>>> fig = plt.figure()
>>> ax = fig.add_subplot(projection='3d')
>>> ax.plot_wireframe(X, Y, lut2(X, Y))
>>> ax.scatter(x, y, z,  'o', color='k', s=48)

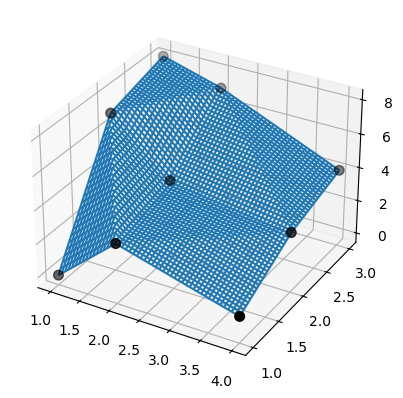
Обратите внимание, что bisplrep делает что-то другое! Он может размещать узлы сплайна вне данных.

Для иллюстрации рассмотрим те же данные из предыдущего примера:

>>> tck = bisplrep(x, y, z, kx=1, ky=1, s=0)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(projection='3d')
>>> xx = np.linspace(min(x), max(x))
>>> yy = np.linspace(min(y), max(y))
>>> X, Y = np.meshgrid(xx, yy)
>>> Z = bisplev(xx, yy, tck)
>>> Z = Z.reshape(*X.shape).T
>>> ax.plot_wireframe(X, Y, Z, rstride=2, cstride=2)
>>> ax.scatter(x, y, z,  'o', color='k', s=48)

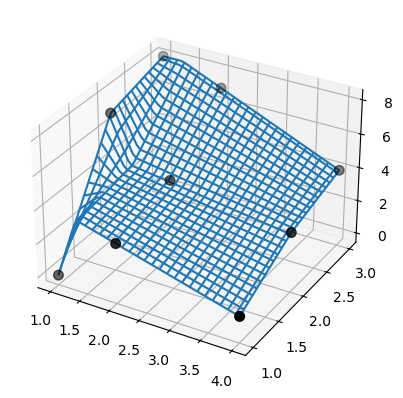
Также, SmoothBivariateSpline не удается интерполировать данные. Снова используйте те же данные из предыдущего примера.

>>> lut = SmoothBivariateSpline(x, y, z, kx=1, ky=1, s=0)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(projection='3d')
>>> xx = np.linspace(min(x), max(x))
>>> yy = np.linspace(min(y), max(y))
>>> X, Y = np.meshgrid(xx, yy)
>>> ax.plot_wireframe(X, Y, lut(xx, yy).T, rstride=4, cstride=4)
>>> ax.scatter(x, y, z,  'o', color='k', s=48)

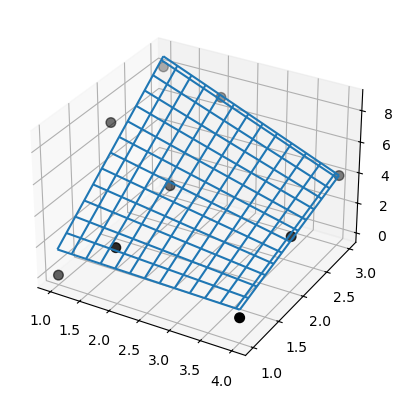
Обратите внимание, что оба SmoothBivariateSpline и bisplrep результаты содержат артефакты, в отличие от LinearNDInterpolators. Проблемы, проиллюстрированные здесь, были зарегистрированы для линейной интерполяции, однако механизм выбора узлов FITPACK не гарантирует избежания любой из этих проблем для поверхностей сплайнов более высокого порядка (например, кубических).