Советы и рекомендации по экстраполяции#
Обработка экстраполяции — вычисление интерполяторов в точках запроса вне области интерполированных данных — не полностью согласована между различными процедурами в scipy.interpolate. Разные интерполяторы используют разные наборы ключевых аргументов для управления поведением вне области данных: некоторые используют extrapolate=True/False/None, некоторые
позволяют fill_value ключевое слово. Обратитесь к документации API для подробностей по каждой конкретной интерполяционной процедуре.
В зависимости от конкретной задачи доступные ключевые слова могут быть достаточными или нет. Особое внимание следует уделить экстраполяции нелинейных интерполянтов. Очень часто экстраполированные результаты становятся менее осмысленными с увеличением расстояния от области данных. Это, конечно, ожидаемо: интерполянт знает только данные внутри области данных.
Когда результаты экстраполяции по умолчанию неадекватны, пользователям нужно реализовать желаемый режим экстраполяции самостоятельно.
В этом руководстве мы рассмотрим несколько рабочих примеров, где продемонстрируем как использование доступных ключевых слов, так и ручную реализацию желаемых режимов экстраполяции. Эти примеры могут быть или не быть применимы к вашей конкретной задаче; они не обязательно являются лучшими практиками; и они намеренно сведены к основным элементам, необходимым для демонстрации главных идей, в надежде, что они послужат вдохновением для вашего подхода к решению вашей конкретной задачи.
interp1d : репликация numpy.interp левое и правое значения заполнения#
TL;DR: Используйте fill_value=(left, right)
numpy.interp использует постоянную экстраполяцию и по умолчанию расширяет первое и последнее значения y массив в интервале интерполяции: выход np.interp(xnew, x, y) является y[0] для
xnew < x[0] и y[-1] для xnew > x[-1].
По умолчанию, interp1d отказывается экстраполировать и вызывает
ValueError при вычислении в точке данных вне
диапазона интерполяции. Это можно отключить с помощью
bounds_error=False аргумент: тогда interp1d устанавливает значения вне диапазона
с помощью fill_value, что является nan по умолчанию.
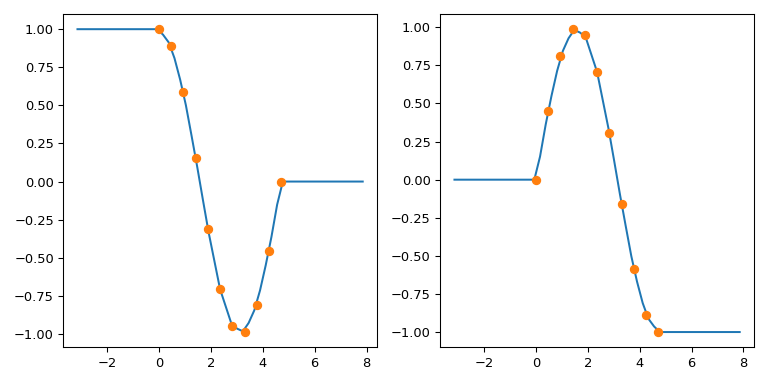
Чтобы имитировать поведение numpy.interp с interp1d, вы можете использовать
тот факт, что он поддерживает 2-кортеж в качестве fill_value. Затем элементы кортежа используются для заполнения xnew < min(x) и x > max(x),
соответственно. Для многомерных y, эти элементы должны иметь
ту же форму, что и y или быть транслируемыми к нему.
Для иллюстрации:
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
x = np.linspace(0, 1.5*np.pi, 11)
y = np.column_stack((np.cos(x), np.sin(x))) # y.shape is (11, 2)
func = interp1d(x, y,
axis=0, # interpolate along columns
bounds_error=False,
kind='linear',
fill_value=(y[0], y[-1]))
xnew = np.linspace(-np.pi, 2.5*np.pi, 51)
ynew = func(xnew)
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
ax1.plot(xnew, ynew[:, 0])
ax1.plot(x, y[:, 0], 'o')
ax2.plot(xnew, ynew[:, 1])
ax2.plot(x, y[:, 1], 'o')
plt.tight_layout()
CubicSpline расширяет граничные условия#
CubicSpline требует двух дополнительных граничных условий, которые контролируются параметром bc_type параметр. Этот параметр может либо перечислять
явные значения производных на границах, либо использовать полезные псевдонимы. Например, bc_type="clamped" устанавливает первые производные в ноль,
bc_type="natural" устанавливает вторые производные в ноль (два других
распознаваемых строковых значения — "periodic" и "not-a-knot")
Хотя экстраполяция контролируется граничным условием,
соотношение не очень интуитивно понятно. Например, можно ожидать, что для
bc_type="natural", экстраполяция линейна. Это ожидание слишком строгое: каждое граничное условие задает производные в единственной точке, на границе только. Экстраполяция выполняется из первого и последнего полиномиальных сегментов, которые — для естественного сплайна — являются кубическими с нулевой второй производной в данной точке.
Еще один способ понять, почему это ожидание слишком сильное — рассмотреть набор данных всего с тремя точками, где сплайн состоит из двух полиномиальных частей. Для линейной экстраполяции это ожидание подразумевает, что обе эти части линейны. Но тогда две линейные части не могут совпадать в средней точке с непрерывной 2-й производной! (Конечно, если только все три точки данных действительно лежат на одной прямой).
Для иллюстрации поведения мы рассматриваем синтетический набор данных и сравниваем несколько граничных условий:
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CubicSpline
xs = [1, 2, 3, 4, 5, 6, 7, 8]
ys = [4.5, 3.6, 1.6, 0.0, -3.3, -3.1, -1.8, -1.7]
notaknot = CubicSpline(xs, ys, bc_type='not-a-knot')
natural = CubicSpline(xs, ys, bc_type='natural')
clamped = CubicSpline(xs, ys, bc_type='clamped')
xnew = np.linspace(min(xs) - 4, max(xs) + 4, 101)
splines = [notaknot, natural, clamped]
titles = ['not-a-knot', 'natural', 'clamped']
fig, axs = plt.subplots(3, 3, figsize=(12, 12))
for i in [0, 1, 2]:
for j, spline, title in zip(range(3), splines, titles):
axs[i, j].plot(xs, spline(xs, nu=i),'o')
axs[i, j].plot(xnew, spline(xnew, nu=i),'-')
axs[i, j].set_title(f'{title}, deriv={i}')
plt.tight_layout()
plt.show()
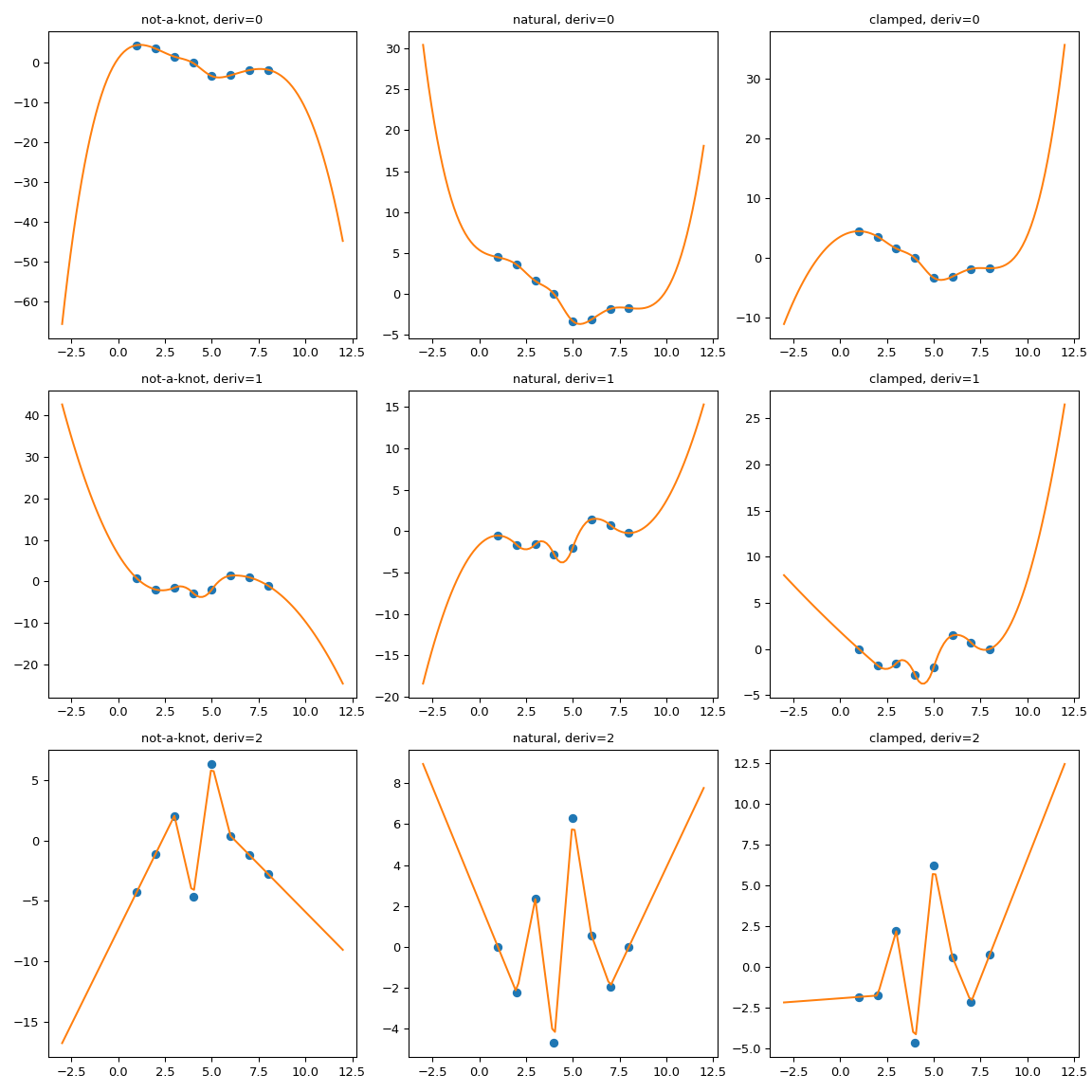
Чётко видно, что естественный сплайн действительно имеет нулевую вторую
производную на границах, но экстраполяция нелинейна.
bc_type="clamped" показывает аналогичное поведение: первые производные равны
нулю только точно на границе. Во всех случаях экстраполяция выполняется путем
расширения первого и последнего полиномиальных участков сплайна, какими бы они
ни были.
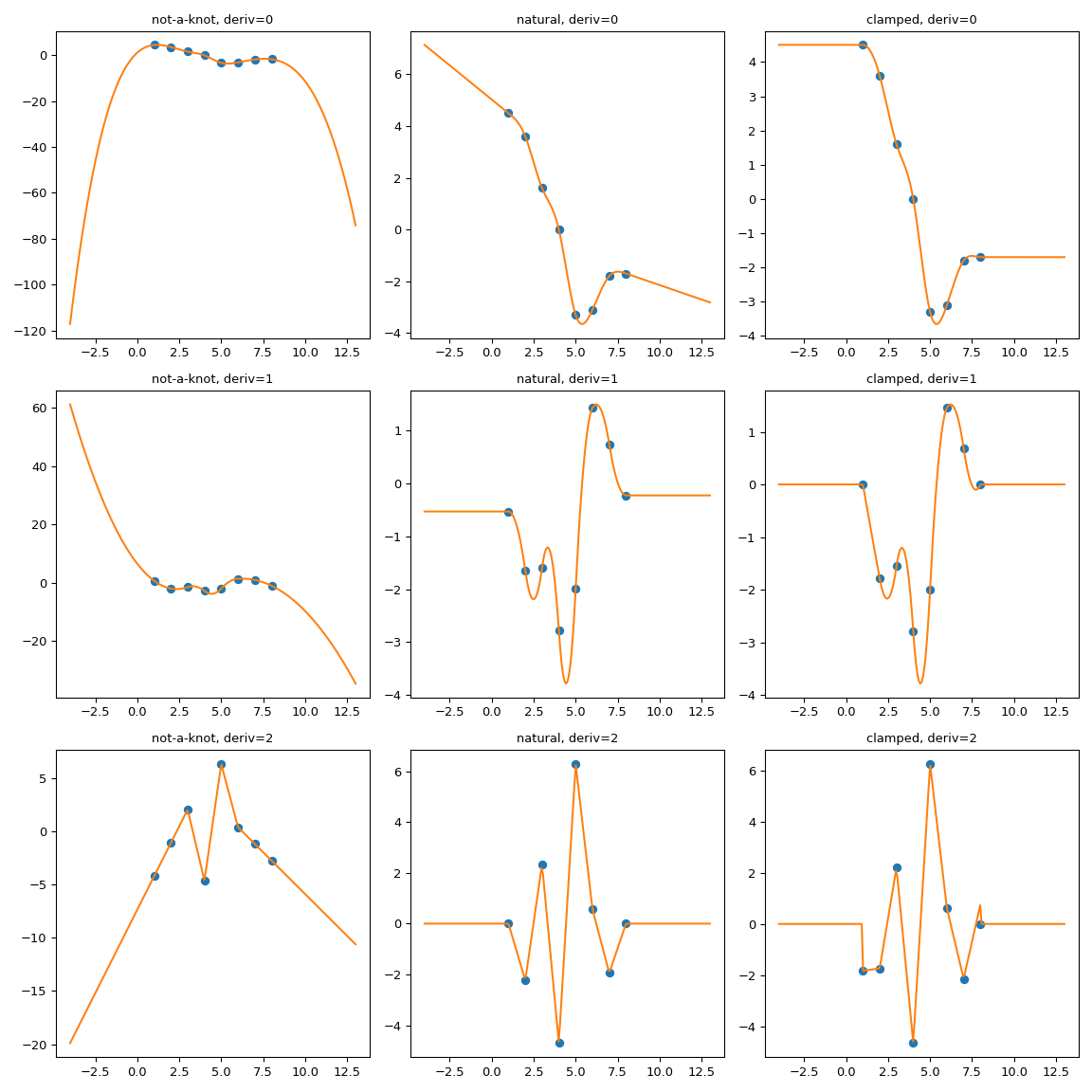
Один из возможных способов принудительной экстраполяции — расширить область интерполяции, добавив первый и последний полиномиальные сегменты с желаемыми свойствами.
Здесь мы используем extend метод CubicSpline суперкласс,
PPoly, чтобы добавить две дополнительные точки разрыва и убедиться, что дополнительные
полиномиальные куски сохраняют значения производных. Затем
экстраполяция продолжается с использованием этих двух дополнительных интервалов.
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CubicSpline
def add_boundary_knots(spline):
"""
Add knots infinitesimally to the left and right.
Additional intervals are added to have zero 2nd and 3rd derivatives,
and to maintain the first derivative from whatever boundary condition
was selected. The spline is modified in place.
"""
# determine the slope at the left edge
leftx = spline.x[0]
lefty = spline(leftx)
leftslope = spline(leftx, nu=1)
# add a new breakpoint just to the left and use the
# known slope to construct the PPoly coefficients.
leftxnext = np.nextafter(leftx, leftx - 1)
leftynext = lefty + leftslope*(leftxnext - leftx)
leftcoeffs = np.array([0, 0, leftslope, leftynext])
spline.extend(leftcoeffs[..., None], np.r_[leftxnext])
# repeat with additional knots to the right
rightx = spline.x[-1]
righty = spline(rightx)
rightslope = spline(rightx,nu=1)
rightxnext = np.nextafter(rightx, rightx + 1)
rightynext = righty + rightslope * (rightxnext - rightx)
rightcoeffs = np.array([0, 0, rightslope, rightynext])
spline.extend(rightcoeffs[..., None], np.r_[rightxnext])
xs = [1, 2, 3, 4, 5, 6, 7, 8]
ys = [4.5, 3.6, 1.6, 0.0, -3.3, -3.1, -1.8, -1.7]
notaknot = CubicSpline(xs,ys, bc_type='not-a-knot')
# not-a-knot does not require additional intervals
natural = CubicSpline(xs,ys, bc_type='natural')
# extend the natural natural spline with linear extrapolating knots
add_boundary_knots(natural)
clamped = CubicSpline(xs,ys, bc_type='clamped')
# extend the clamped spline with constant extrapolating knots
add_boundary_knots(clamped)
xnew = np.linspace(min(xs) - 5, max(xs) + 5, 201)
fig, axs = plt.subplots(3, 3,figsize=(12,12))
splines = [notaknot, natural, clamped]
titles = ['not-a-knot', 'natural', 'clamped']
for i in [0, 1, 2]:
for j, spline, title in zip(range(3), splines, titles):
axs[i, j].plot(xs, spline(xs, nu=i),'o')
axs[i, j].plot(xnew, spline(xnew, nu=i),'-')
axs[i, j].set_title(f'{title}, deriv={i}')
plt.tight_layout()
plt.show()
Вручную реализовать асимптотику#
Предыдущий трюк расширения области интерполяции основан на
CubicSpline.extend метод. Более общая альтернатива — реализовать обертку, которая явно обрабатывает поведение за пределами границ. Рассмотрим рабочий пример.
Настройка#
Предположим, мы хотим решить при заданном значении \(a\) уравнение
(Одно из применений, где появляются такие уравнения — решение для энергетических уровней квантовой частицы). Для простоты рассмотрим только \(x\in (0, \pi/2)\).
Решение этого уравнения однажды просто:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import brentq
def f(x, a):
return a*x - 1/np.tan(x)
a = 3
x0 = brentq(f, 1e-16, np.pi/2, args=(a,)) # here we shift the left edge
# by a machine epsilon to avoid
# a division by zero at x=0
xx = np.linspace(0.2, np.pi/2, 101)
plt.plot(xx, a*xx, '--')
plt.plot(xx, 1/np.tan(xx), '--')
plt.plot(x0, a*x0, 'o', ms=12)
plt.text(0.1, 0.9, fr'$x_0 = {x0:.3f}$',
transform=plt.gca().transAxes, fontsize=16)
plt.show()
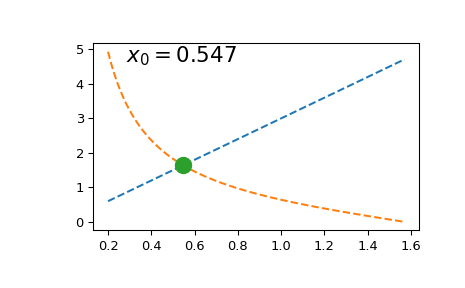
Однако, если нам нужно решить её несколько раз (например, чтобы найти ряд
корней из-за периодичности tan функция), повторные вызовы
scipy.optimize.brentq становятся непомерно дорогими.
Чтобы обойти эту трудность, мы табулируем \(y = ax - 1/\tan{x}\) и интерполировать её на табличной сетке. Фактически, мы будем использовать обратный интерполяция: мы интерполируем значения \(x\) против \(у\). Таким образом, решение исходного уравнения сводится просто к вычислению интерполированной функции в нуле \(y\) аргумент.
Чтобы улучшить точность интерполяции, мы будем использовать знание производных табулированной функции. Мы будем использовать
BPoly.from_derivatives для построения кубического интерполянта (эквивалентно, мы могли бы использовать CubicHermiteSpline)
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import BPoly
def f(x, a):
return a*x - 1/np.tan(x)
xleft, xright = 0.2, np.pi/2
x = np.linspace(xleft, xright, 11)
fig, ax = plt.subplots(1, 2, figsize=(12, 4))
for j, a in enumerate([3, 93]):
y = f(x, a)
dydx = a + 1./np.sin(x)**2 # d(ax - 1/tan(x)) / dx
dxdy = 1 / dydx # dx/dy = 1 / (dy/dx)
xdx = np.c_[x, dxdy]
spl = BPoly.from_derivatives(y, xdx) # inverse interpolation
yy = np.linspace(f(xleft, a), f(xright, a), 51)
ax[j].plot(yy, spl(yy), '--')
ax[j].plot(y, x, 'o')
ax[j].set_xlabel(r'$y$')
ax[j].set_ylabel(r'$x$')
ax[j].set_title(rf'$a = {a}$')
ax[j].plot(0, spl(0), 'o', ms=12)
ax[j].text(0.1, 0.85, fr'$x_0 = {spl(0):.3f}$',
transform=ax[j].transAxes, fontsize=18)
ax[j].grid(True)
plt.tight_layout()
plt.show()
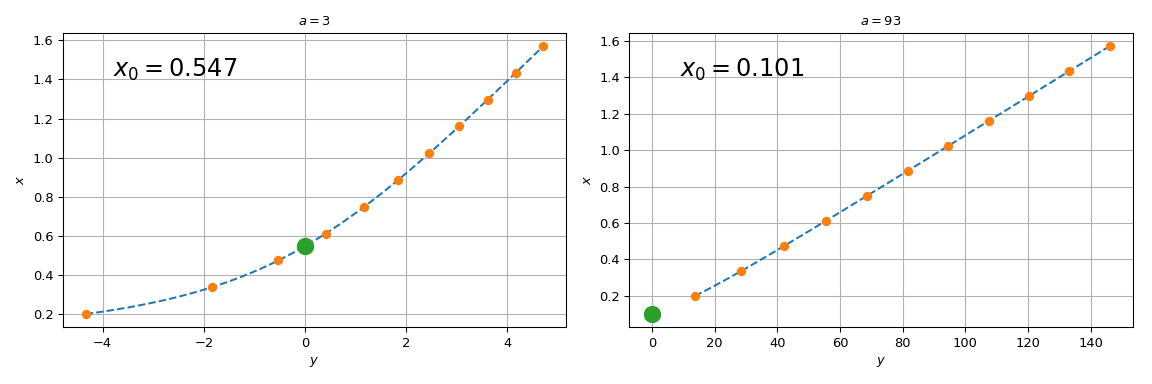
Заметим, что для \(a=3\), spl(0) согласуется с brentq вызов выше, в то время как для \(a = 93\), разница существенна. Причина, по которой процедура начинает давать сбой для больших \(a\) заключается в том, что
прямая линия \(y = ax\) стремится к вертикальной оси, а
корень исходного уравнения стремится к \(x=0\). Поскольку мы
табулировали исходную функцию на конечной сетке, spl(0) включает
экстраполяцию для слишком больших значений \(a\). Полагаться на экстраполяцию склонно к потере точности, и этого лучше избегать.
Используйте известные асимптотики#
Рассматривая исходное уравнение, мы отмечаем, что для \(x\to 0\), \(\tan(x) = x + O(x^3)\), и исходное уравнение становится
так что \(x_0 \approx 1/\sqrt{a}\) для \(a \gg 1\).
Мы будем использовать это для создания класса, который переключается с интерполяции на использование этого известного асимптотического поведения для данных вне диапазона. Базовая реализация может выглядеть так
class RootWithAsymptotics:
def __init__(self, a):
# construct the interpolant
xleft, xright = 0.2, np.pi/2
x = np.linspace(xleft, xright, 11)
y = f(x, a)
dydx = a + 1./np.sin(x)**2 # d(ax - 1/tan(x)) / dx
dxdy = 1 / dydx # dx/dy = 1 / (dy/dx)
# inverse interpolation
self.spl = BPoly.from_derivatives(y, np.c_[x, dxdy])
self.a = a
def root(self):
out = self.spl(0)
asympt = 1./np.sqrt(self.a)
return np.where(spl.x.min() < asympt, out, asympt)
И затем
>>> r = RootWithAsymptotics(93)
>>> r.root()
array(0.10369517)
что отличается от экстраполированного результата и согласуется с brentq вызов.
Обратите внимание, что эта реализация намеренно упрощена. С точки зрения API, вы можете вместо этого реализовать __call__ метод
так, чтобы полная зависимость от x на y доступен. С числовой точки зрения требуется дополнительная работа, чтобы убедиться, что переход между интерполяцией и асимптотикой происходит достаточно глубоко в асимптотическом режиме, чтобы результирующая функция была достаточно гладкой в точке перехода.
Также в этом примере мы искусственно ограничили задачу только
одним интервалом периодичности tan функция, и только
обрабатывалась \(a > 0\). Для отрицательных значений \(a\), нам потребуется реализовать другие асимптотики, для \(x\to \pi\).
Однако основная идея та же.
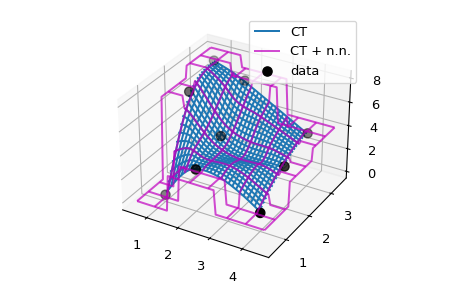
Экстраполяция в D > 1#
Основная идея реализации экстраполяции вручную в классе-обёртке
или функции может быть легко обобщена на более высокие размерности. В качестве
примера мы рассматриваем C1-гладкую интерполяционную задачу для 2D данных с использованием
CloughTocher2DInterpolator. По умолчанию он заполняет значения вне границ nans, и мы хотим вместо этого использовать для каждой точки запроса значение её ближайшего соседа.
Поскольку CloughTocher2DInterpolator принимает либо 2D данные, либо триангуляцию Делоне
точек данных; эффективный способ поиска ближайших
соседей точек запроса — построить триангуляцию (используя
scipy.spatial инструменты) и используйте его для поиска ближайших соседей на выпуклой оболочке данных.
Вместо этого мы будем использовать более простой, наивный метод и полагаться на цикл по всему набору данных с использованием трансляции NumPy.
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CloughTocher2DInterpolator as CT
def my_CT(xy, z):
"""CT interpolator + nearest-neighbor extrapolation.
Parameters
----------
xy : ndarray, shape (npoints, ndim)
Coordinates of data points
z : ndarray, shape (npoints)
Values at data points
Returns
-------
func : callable
A callable object which mirrors the CT behavior,
with an additional neareast-neighbor extrapolation
outside of the data range.
"""
x = xy[:, 0]
y = xy[:, 1]
f = CT(xy, z)
# this inner function will be returned to a user
def new_f(xx, yy):
# evaluate the CT interpolator. Out-of-bounds values are nan.
zz = f(xx, yy)
nans = np.isnan(zz)
if nans.any():
# for each nan point, find its nearest neighbor
inds = np.argmin(
(x[:, None] - xx[nans])**2 +
(y[:, None] - yy[nans])**2
, axis=0)
# ... and use its value
zz[nans] = z[inds]
return zz
return new_f
# Now illustrate the difference between the original ``CT`` interpolant
# and ``my_CT`` on a small example:
x = np.array([1, 1, 1, 2, 2, 2, 4, 4, 4])
y = np.array([1, 2, 3, 1, 2, 3, 1, 2, 3])
z = np.array([0, 7, 8, 3, 4, 7, 1, 3, 4])
xy = np.c_[x, y]
lut = CT(xy, z)
lut2 = my_CT(xy, z)
X = np.linspace(min(x) - 0.5, max(x) + 0.5, 71)
Y = np.linspace(min(y) - 0.5, max(y) + 0.5, 71)
X, Y = np.meshgrid(X, Y)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_wireframe(X, Y, lut(X, Y), label='CT')
ax.plot_wireframe(X, Y, lut2(X, Y), color='m',
cstride=10, rstride=10, alpha=0.7, label='CT + n.n.')
ax.scatter(x, y, z, 'o', color='k', s=48, label='data')
ax.legend()
plt.tight_layout()