Тест тау Кендалла#
Тау Кендалла — это мера соответствия между двумя ранжировками.
Рассмотрим следующие данные из [1], который изучал взаимосвязь между свободным пролином (аминокислотой) и общим коллагеном (белком, часто встречающимся в соединительной ткани) в больной человеческой печени.
The x и y массивы ниже записывают измерения двух соединений.
Наблюдения парные: каждое измерение свободного пролина было взято из той же
печени, что и измерение общего коллагена с тем же индексом.
import numpy as np
# total collagen (mg/g dry weight of liver)
x = np.array([7.1, 7.1, 7.2, 8.3, 9.4, 10.5, 11.4])
# free proline (μ mole/g dry weight of liver)
y = np.array([2.8, 2.9, 2.8, 2.6, 3.5, 4.6, 5.0])
Эти данные были проанализированы в [2] используя коэффициент корреляции Спирмена, статистику, похожую на тау Кендалла, поскольку она также чувствительна к порядковой корреляции между выборками. Проведём аналогичное исследование с использованием Kendall's tau.
from scipy import stats
res = stats.kendalltau(x, y)
res.statistic
np.float64(0.5499999999999999)
Значение этой статистики стремится быть высоким (близким к 1) для выборок с сильно положительной порядковой корреляцией, низким (близким к -1) для выборок с сильно отрицательной порядковой корреляцией и малым по величине (близким к нулю) для выборок со слабой порядковой корреляцией.
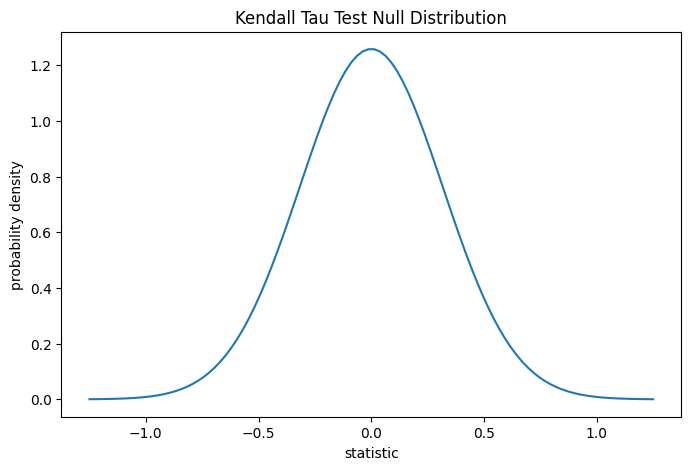
Тест выполняется путем сравнения наблюдаемого значения статистики с нулевым распределением: распределением значений статистики, полученных при нулевой гипотезе о том, что измерения общего коллагена и свободного пролина независимы.
Для этого теста нулевое распределение для больших выборок без связей
аппроксимируется нормальным распределением с дисперсией
(2*(2*n + 5))/(9*n*(n - 1)), где n = len(x).
import matplotlib.pyplot as plt
n = len(x) # len(x) == len(y)
var = (2*(2*n + 5))/(9*n*(n - 1))
dist = stats.norm(scale=np.sqrt(var))
z_vals = np.linspace(-1.25, 1.25, 100)
pdf = dist.pdf(z_vals)
fig, ax = plt.subplots(figsize=(8, 5))
def plot(ax): # we'll reuse this
ax.plot(z_vals, pdf)
ax.set_title("Kendall Tau Test Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
plot(ax)
plt.show()
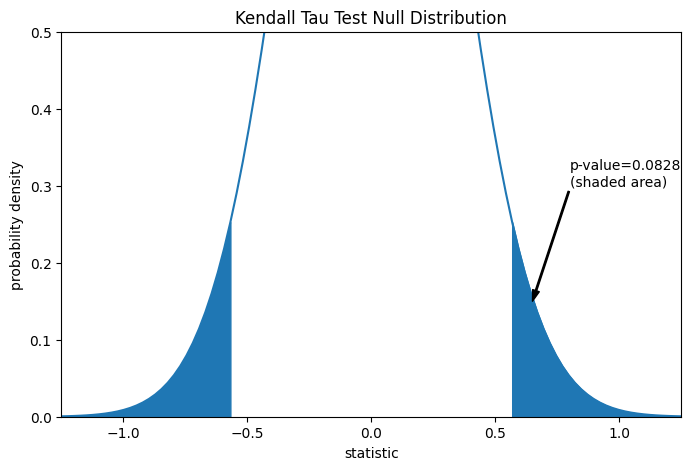
Сравнение количественно оценивается p-значением: долей значений в нулевом распределении, столь же экстремальных или более экстремальных, чем наблюдаемое значение статистики. В двустороннем тесте, в котором статистика положительна, элементы нулевого распределения больше преобразованной статистики и элементы нулевого распределения меньше отрицательного наблюдаемой статистики оба считаются "более экстремальными".
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
pvalue = dist.cdf(-res.statistic) + dist.sf(res.statistic)
annotation = (f'p-value={pvalue:.4f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (0.65, 0.15), (0.8, 0.3), arrowprops=props)
i = z_vals >= res.statistic
ax.fill_between(z_vals[i], y1=0, y2=pdf[i], color='C0')
i = z_vals <= -res.statistic
ax.fill_between(z_vals[i], y1=0, y2=pdf[i], color='C0')
ax.set_xlim(-1.25, 1.25)
ax.set_ylim(0, 0.5)
plt.show()
res.pvalue
np.float64(0.09108705741631495)
Обратите внимание, что есть небольшое расхождение между затенённой областью кривой и p-значением, возвращаемым scipy.stats.kendalltau. Это происходит потому, что наши данные
имеют связи, и мы пренебрегли поправкой на связи к дисперсии нулевого распределения,
которая scipy.stats.kendalltau выполняет. Для выборок без совпадений затенённые области нашего графика и p-значение, возвращаемое
scipy.stats.kendalltau будет точно совпадать.
Если p-значение «маленькое» — то есть если существует низкая вероятность выборки данных из независимых распределений, которые дают такое экстремальное значение статистики — это может рассматриваться как свидетельство против нулевой гипотезы в пользу альтернативной: распределение общего коллагена и свободного пролина не независимы. Обратите внимание, что:
Обратное неверно; то есть тест не используется для предоставления доказательств в пользу нулевой гипотезы.
Порог для значений, которые будут считаться «малыми», — это выбор, который следует сделать до анализа данных [3] с учетом рисков как ложноположительных (ошибочное отклонение нулевой гипотезы), так и ложноотрицательных (неспособность отклонить ложную нулевую гипотезу).
Маленькие p-значения не являются доказательством большой эффект; скорее, они могут только предоставить доказательства «значимого» эффекта, означающего, что они маловероятны при нулевой гипотезе.
Для выборок без связей умеренного размера, scipy.stats.kendalltau может точно вычислить p-значение. Однако при наличии связей,
scipy.stats.kendalltau прибегает к асимптотическому приближению.
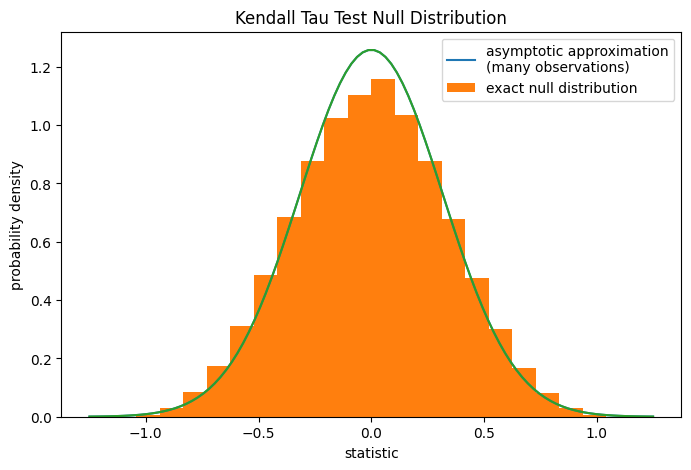
Тем не менее, мы можем использовать перестановочный тест для точного вычисления
нулевого распределения: В соответствии с нулевой гипотезой о независимости общего коллагена и свободного пролина,
каждое измерение свободного пролина было одинаково вероятно наблюдаться
с любым из измерений общего коллагена. Поэтому мы можем
сформировать точный нулевое распределение путем вычисления статистики для каждой
возможной пары элементов между x и y.
def statistic(x): # explore all possible pairings by permuting `x`
return stats.kendalltau(x, y).statistic # ignore pvalue
ref = stats.permutation_test((x,), statistic,
permutation_type='pairings')
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
bins = np.linspace(-1.25, 1.25, 25)
ax.hist(ref.null_distribution, bins=bins, density=True)
ax.legend(['asymptotic approximation\n(many observations)',
'exact null distribution'])
plot(ax)
plt.show()
ref.pvalue
np.float64(0.12222222222222222)
Обратите внимание, что существует значительное расхождение между точным p-значением, вычисленным
здесь, и аппроксимацией, возвращаемой scipy.stats.kendalltau выше. Для малых выборок со связями рассмотрите выполнение перестановочного теста для более точных результатов.