Тест на эксцесс#
Тест на эксцесс scipy.stats.kurtosistest функция проверяет нулевую гипотезу о том, что эксцесс генеральной совокупности, из которой была взята выборка, соответствует нормальному распределению.
Предположим, мы хотим сделать вывод из измерений, отличаются ли веса взрослых мужчин
в медицинском исследовании от нормального распределения [1]. Веса (фунты)
записываются в массив x ниже.
import numpy as np
x = np.array([148, 154, 158, 160, 161, 162, 166, 170, 182, 195, 236])
Тест эксцесса из [2] начинается с вычисления статистики на основе выборочного (избыточного/Фишера) эксцесса.
from scipy import stats
res = stats.kurtosistest(x)
res.statistic
np.float64(2.3048235214240873)
(Тест предупреждает, что в нашей выборке слишком мало наблюдений для выполнения теста. Мы вернемся к этому в конце примера.) Поскольку нормальные распределения имеют нулевой эксцесс (по определению), величина этой статистики обычно мала для выборок, взятых из нормального распределения.
Тест выполняется путем сравнения наблюдаемого значения статистики с нулевым распределением: распределением значений статистики, полученным при нулевой гипотезе о том, что веса были взяты из нормального распределения.
Для этого теста нулевое распределение статистики для очень больших выборок является стандартным нормальным распределением.
import matplotlib.pyplot as plt
dist = stats.norm()
kt_val = np.linspace(-5, 5, 100)
pdf = dist.pdf(kt_val)
fig, ax = plt.subplots(figsize=(8, 5))
def kt_plot(ax): # we'll reuse this
ax.plot(kt_val, pdf)
ax.set_title("Kurtosis Test Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
kt_plot(ax)
plt.show()
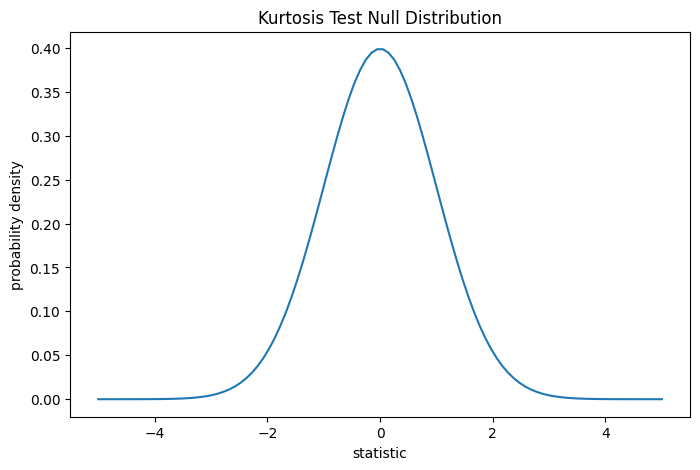
Сравнение количественно оценивается с помощью p-значения: доли значений в нулевом распределении, столь же или более экстремальных, чем наблюдаемое значение статистики. В двустороннем тесте, где статистика положительна, элементы нулевого распределения, превышающие наблюдаемую статистику, и элементы нулевого распределения, меньшие отрицательного значения наблюдаемой статистики, оба считаются «более экстремальными».
fig, ax = plt.subplots(figsize=(8, 5))
kt_plot(ax)
pvalue = dist.cdf(-res.statistic) + dist.sf(res.statistic)
annotation = (f'p-value={pvalue:.3f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (3, 0.005), (3.25, 0.02), arrowprops=props)
i = kt_val >= res.statistic
ax.fill_between(kt_val[i], y1=0, y2=pdf[i], color='C0')
i = kt_val <= -res.statistic
ax.fill_between(kt_val[i], y1=0, y2=pdf[i], color='C0')
ax.set_xlim(-5, 5)
ax.set_ylim(0, 0.1)
plt.show()
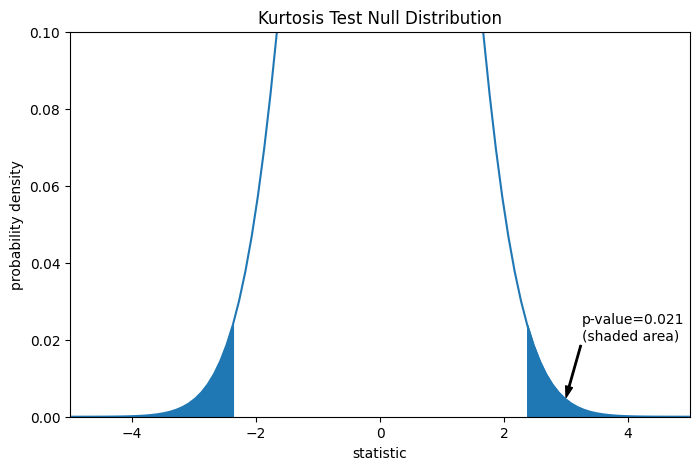
res.pvalue
np.float64(0.0211764592113868)
Если p-значение «маленькое» - то есть если существует низкая вероятность выборки данных из нормально распределенной совокупности, которая дает такое экстремальное значение статистики - это может быть принято как свидетельство против нулевой гипотезы в пользу альтернативы: веса не были взяты из нормального распределения. Обратите внимание, что:
Обратное неверно; то есть тест не используется для предоставления доказательств в пользу нулевой гипотезы.
Порог для значений, которые будут считаться «малыми», — это выбор, который следует сделать до анализа данных [3] с учетом рисков как ложноположительных (ошибочное отклонение нулевой гипотезы), так и ложноотрицательных (неспособность отклонить ложную нулевую гипотезу).
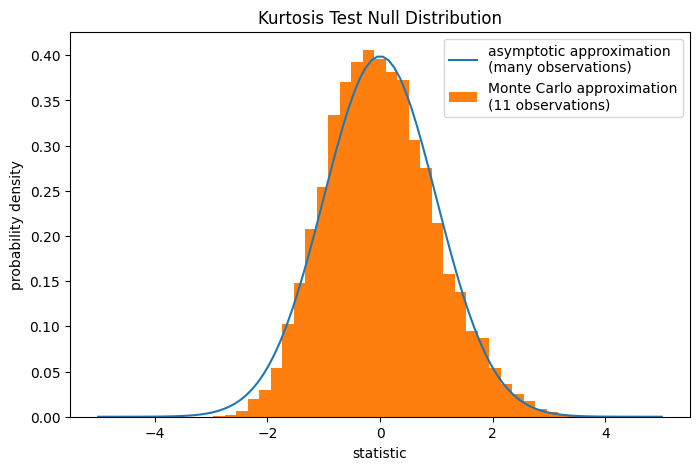
Обратите внимание, что стандартное нормальное распределение даёт асимптотическое приближение
нулевого распределения; оно точно только для выборок с большим
количеством наблюдений. Это причина, по которой мы получили предупреждение в начале
примера; наша выборка довольно мала. В этом случае,
scipy.stats.monte_carlo_test может дать более точное, хотя и стохастическое, приближение точного p-значения.
def statistic(x, axis):
# get just the skewtest statistic; ignore the p-value
return stats.kurtosistest(x, axis=axis).statistic
res = stats.monte_carlo_test(x, stats.norm.rvs, statistic)
fig, ax = plt.subplots(figsize=(8, 5))
kt_plot(ax)
ax.hist(res.null_distribution, np.linspace(-5, 5, 50),
density=True)
ax.legend(['asymptotic approximation\n(many observations)',
'Monte Carlo approximation\n(11 observations)'])
plt.show()
res.pvalue
np.float64(0.0274)
Более того, несмотря на их стохастическую природу, p-значения, вычисленные таким образом, могут быть использованы для точного контроля уровня ложных отклонений нулевой гипотезы [4].