Тест Шапиро-Уилка на нормальность#

Предположим, мы хотим сделать вывод из измерений, отличаются ли веса взрослых мужчин в медицинском исследовании от нормального распределения [1]. Веса (фунты) записываются в массив x ниже.

import numpy as np
x = np.array([148, 154, 158, 160, 161, 162, 166, 170, 182, 195, 236])

Тест на нормальность scipy.stats.shapiro of [1] и [2] начинается с вычисления статистики на основе взаимосвязи между наблюдениями и ожидаемыми порядковыми статистиками нормального распределения.

from scipy import stats
res = stats.shapiro(x)
res.statistic

np.float64(0.7888146948631716)

Значение этой статистики обычно высокое (близко к 1) для выборок, взятых из нормального распределения.

Тест выполняется путём сравнения наблюдаемого значения статистики с нулевым распределением: распределением значений статистики, сформированным при нулевой гипотезе, что веса были взяты из нормального распределения. Для этого теста на нормальность нулевое распределение нелегко вычислить точно, поэтому оно обычно аппроксимируется методами Монте-Карло, то есть путём генерации многих выборок того же размера, что и x из нормального распределения и вычисления значений статистики для каждого.

def statistic(x):
    # Get only the `shapiro` statistic; ignore its p-value
    return stats.shapiro(x).statistic
ref = stats.monte_carlo_test(x, stats.norm.rvs, statistic,
                             alternative='less')
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 5))
bins = np.linspace(0.65, 1, 50)

def plot(ax):  # we'll reuse this
    ax.hist(ref.null_distribution, density=True, bins=bins)
    ax.set_title("Shapiro-Wilk Test Null Distribution \n"
                 "(Monte Carlo Approximation, 11 Observations)")
    ax.set_xlabel("statistic")
    ax.set_ylabel("probability density")

plot(ax)
plt.show()

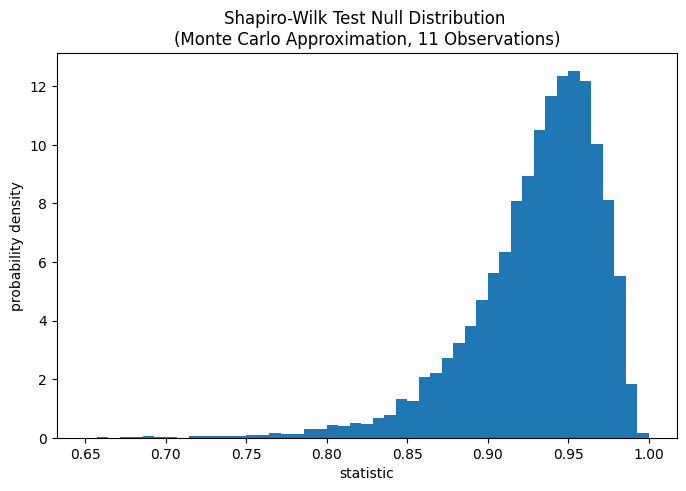
../../_images/c9a5287e20ee08b1094a8d760d8dc7a106bcdc50995e50d747444ab5b8499e79.png

Сравнение количественно оценивается p-значением: долей значений в нулевом распределении, меньших или равных наблюдаемому значению статистики.

fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
annotation = (f'p-value={res.pvalue:.6f}\n(highlighted area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (0.75, 0.1), (0.68, 0.7), arrowprops=props)
i_extreme = np.where(bins <= res.statistic)[0]
for i in i_extreme:
    ax.patches[i].set_color('C1')
plt.xlim(0.65, 0.9)
plt.ylim(0, 4)
plt.show()

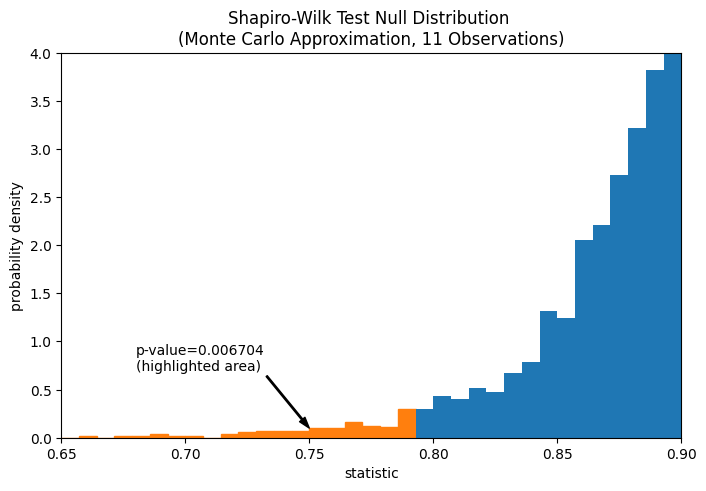
../../_images/eda620ecf2954c373bc6109794e07476aa07ddddf039864ec0cc176f5abddd64.png

res.pvalue

np.float64(0.006703814061898823)

Если p-значение «маленькое» - то есть если существует низкая вероятность выборки данных из нормально распределенной совокупности, которая дает такое экстремальное значение статистики - это может быть принято как свидетельство против нулевой гипотезы в пользу альтернативы: веса не были взяты из нормального распределения. Обратите внимание, что:

Обратное неверно; то есть тест не используется для предоставления доказательств для нулевая гипотеза.
Порог для значений, которые будут считаться «малыми», — это выбор, который следует сделать до анализа данных [3] с учетом рисков как ложноположительных (ошибочное отклонение нулевой гипотезы), так и ложноотрицательных (неспособность отклонить ложную нулевую гипотезу).

Тест Шапиро-Уилка на нормальность#

Ссылки#