Корреляция Пирсона#
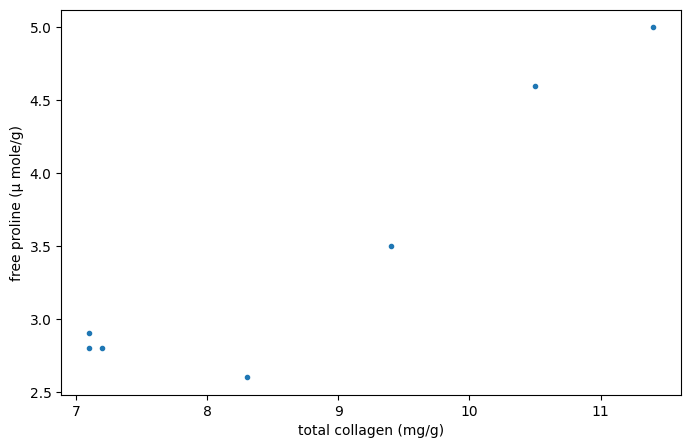
Рассмотрим следующие данные из [1], который изучал взаимосвязь между свободным пролином (аминокислотой) и общим коллагеном (белком, часто встречающимся в соединительной ткани) в больной печени человека.
The x и y массивы ниже содержат измерения двух соединений. Наблюдения парные: каждое измерение свободного пролина было взято из той же печени, что и измерение общего коллагена с тем же индексом.
import numpy as np
# total collagen (mg/g dry weight of liver)
x = np.array([7.1, 7.1, 7.2, 8.3, 9.4, 10.5, 11.4])
# free proline (μ mole/g dry weight of liver)
y = np.array([2.8, 2.9, 2.8, 2.6, 3.5, 4.6, 5.0])
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 5))
ax.plot(x, y, '.')
ax.set_xlabel("total collagen (mg/g)")
ax.set_ylabel("free proline (μ mole/g)")
plt.show()
Эти данные были проанализированы в [2] используя коэффициент корреляции Спирмена, статистику, чувствительную к монотонной корреляции между выборками. Здесь мы проанализируем данные с использованием коэффициента корреляции Пирсона ({class}scipy.stats.pearsonr`), который чувствителен к линейной корреляции.
from scipy import stats
res = stats.pearsonr(x, y)
res.statistic
np.float64(0.9347467974524514)
Значение этой статистики стремится быть высоким (близким к 1) для выборок с сильно положительной линейной корреляцией, низким (близким к -1) для выборок с сильно отрицательной линейной корреляцией и малым по величине (близким к нулю) для выборок со слабой линейной корреляцией.
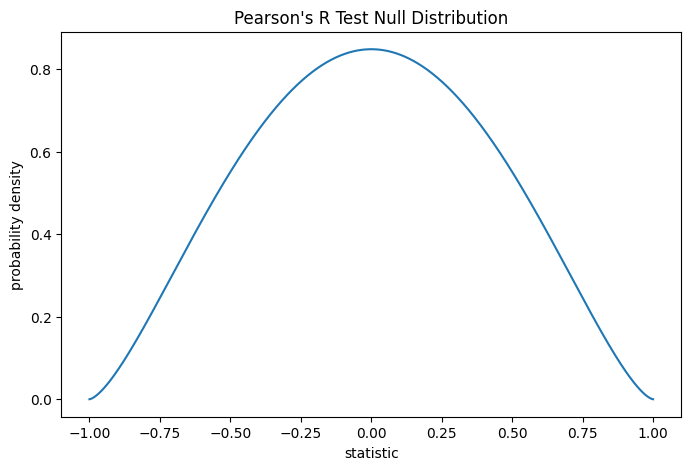
Тест выполняется путем сравнения наблюдаемого значения статистики с нулевым распределением: распределением значений статистики, полученным при нулевой гипотезе, что измерения общего коллагена и свободного пролина взяты из независимых нормальных распределений.
При нулевой гипотезе коэффициент корреляции генеральной совокупности равен нулю, а выборочный коэффициент корреляции следует бета-распределению на интервале \((-1, 1)\) с параметрами формы \(a = b = \frac{n}{2}-1\), где \(n\) — это количество наблюдений в каждой выборке.
n = len(x) # len(x) == len(y)
a = b = n/2 - 1 # shape parameter
loc, scale = -1, 2 # support is (-1, 1)
dist = stats.beta(a=a, b=b, loc=loc, scale=scale)
r_vals = np.linspace(-1, 1, 1000)
pdf = dist.pdf(r_vals)
fig, ax = plt.subplots(figsize=(8, 5))
def plot(ax): # we'll re-use this
ax.plot(r_vals, pdf)
ax.set_title("Pearson's R Test Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
plot(ax)
plt.show()
Сравнение количественно выражается через p-значение: доля значений в нулевом распределении, столь же экстремальных или более экстремальных, чем наблюдаемое значение статистики. В двустороннем тесте, где статистика положительна, элементы нулевого распределения, большие преобразованной статистики, и элементы нулевого распределения, меньшие отрицательного значения наблюдаемой статистики, оба считаются «более экстремальными».
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
rs = res.statistic # original statistic
pvalue = dist.cdf(-rs) + dist.sf(rs)
annotation = (f'p-value={pvalue:.4f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (rs, 0.01), (0.25, 0.1), arrowprops=props)
i = r_vals >= rs
ax.fill_between(r_vals[i], y1=0, y2=pdf[i], color='C0')
i = r_vals <= -rs
ax.fill_between(r_vals[i], y1=0, y2=pdf[i], color='C0')
ax.set_xlim(-1.1, 1.1)
ax.set_ylim(0, 0.9)
plt.show()
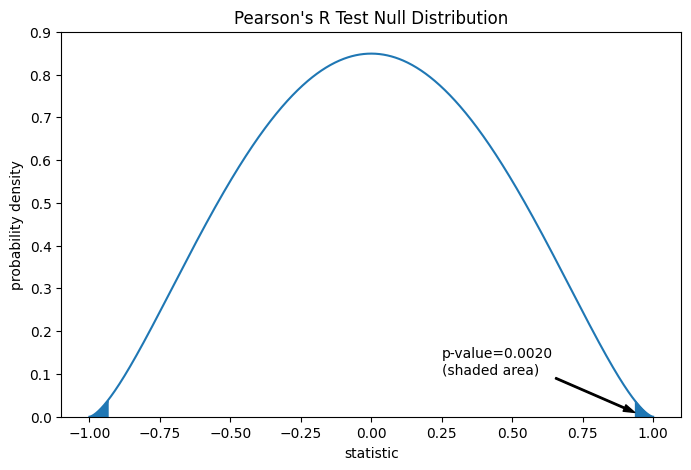
res.pvalue # two-sided p-value
np.float64(0.002016532795489407)
Если p-значение 'маленькое' — то есть если существует низкая вероятность выборки данных из независимых нормальных распределений, которые дают такое экстремальное значение статистики — это может быть принято как свидетельство против нулевой гипотезы в пользу альтернативной: распределения общего коллагена и свободного пролина не являются независимыми. Обратите внимание, что:
Обратное неверно; то есть тест не используется для предоставления доказательств в пользу нулевой гипотезы.
Порог для значений, которые будут считаться "малыми", — это выбор, который должен быть сделан до анализа данных [3] с учётом рисков как ложных срабатываний (ошибочного отклонения нулевой гипотезы), так и пропусков (неотклонения ложной нулевой гипотезы).
Маленькие p-значения не являются доказательством большого эффекта; скорее, они могут лишь свидетельствовать о «значимом» эффекте, означая, что они маловероятны при нулевой гипотезе.
Предположим, что перед проведением эксперимента у авторов были основания предсказывать положительную линейную корреляцию между измерениями общего коллагена и свободного пролина, и что они выбрали оценку правдоподобия нулевой гипотезы против односторонней альтернативы: свободный пролин имеет положительную линейную корреляцию с общим коллагеном. В этом случае только те значения в нулевом распределении, которые равны или больше наблюдаемой статистики, будут считаться более экстремальными.
res = stats.pearsonr(x, y, alternative='greater')
res.statistic
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
pvalue = dist.sf(rs)
annotation = (f'p-value={pvalue:.6f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (rs, 0.01), (0.86, 0.04), arrowprops=props)
i = r_vals >= rs
ax.fill_between(r_vals[i], y1=0, y2=pdf[i], color='C0')
ax.set_xlim(0.85, 1)
ax.set_ylim(0, 0.1)
plt.show()
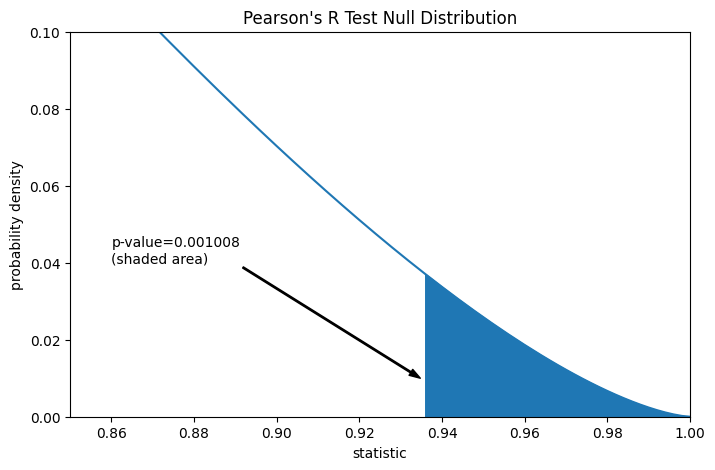
res.pvalue # one-sided p-value; half of the two-sided p-value
np.float64(0.0010082663977447036)
Обратите внимание, что бета-распределение является точным нулевым распределением для выборок любого размера при этой нулевой гипотезе. Мы можем проверить это, вычислив нулевое распределение Монте-Карло: явно рисуя выборки из независимых нормальных распределений и вычисляя статистику Пирсона для каждой пары.
rng = np.random.default_rng(332520619051409741187796892627751113442)
def statistic(x, y, axis):
return stats.pearsonr(x, y, axis=axis).statistic # ignore pvalue
ref = stats.monte_carlo_test((x, y), rvs=(rng.standard_normal, rng.standard_normal),
statistic=statistic, alternative='greater', n_resamples=9999)
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
ax.hist(ref.null_distribution, np.linspace(-1, 1, 26), density=True)
ax.legend(['exact null distribution (independent, normally-distributed observations)',
f'Monte Carlo null distribution \n({len(ref.null_distribution)} permutations)'])
plt.show()
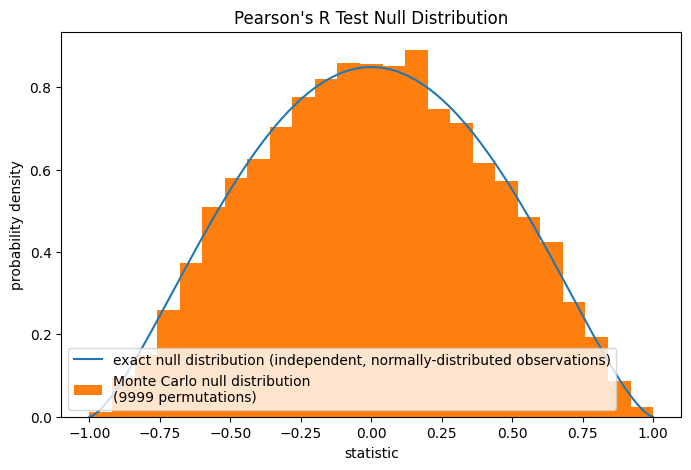
Это часто разумная нулевая гипотеза для проверки, но в других случаях может быть более уместно выполнить перестановочный тест: При нулевой гипотезе, что общий коллаген и свободный пролин независимы (но не обязательно нормально распределены), каждое измерение свободного пролина равновероятно наблюдаться с любым измерением общего коллагена. Поэтому мы можем сформировать точное нулевое распределение, вычислив статистику для каждой возможной пары элементов между x и y. Это нулевое распределение, используемое, когда мы предоставляем pearsonr с method=stats.PermutationMethod().
res = stats.pearsonr(x, y, alternative='greater', method=stats.PermutationMethod())
res.pvalue
np.float64(0.005555555555555556)