Дискретный метод урны с псевдонимами (DAU)#
Требуется: вектор вероятностей (PV) или PMF вместе с конечной областью определения
Скорость:
Настройка: медленная (линейная с длиной вектора)
Сэмплирование: очень быстрое
DAU-выборки из распределений с произвольными, но конечными векторами вероятностей (PV) длины N. Алгоритм основан на изобретательном методе А.Дж. Уокера и требует таблицы размера (как минимум) N. Для каждой генерируемой случайной величины требуется одно случайное число и только одно сравнение. Время настройки для построения таблиц составляет O(N).
>>> import numpy as np
>>> from scipy.stats.sampling import DiscreteAliasUrn
>>>
>>> pv = [0.18, 0.02, 0.8]
>>> urng = np.random.default_rng()
>>> rng = DiscreteAliasUrn(pv, random_state=urng)
>>> rng.rvs()
0 # may vary
По умолчанию вектор вероятностей индексируется, начиная с 0. Однако это можно изменить, передав domain параметр. Когда domain при использовании в комбинации с PV, это приводит к перемещению распределения из (0, len(pv)) to (domain[0], domain[0] + len(pv)).
domain[1] игнорируется в этом случае.
>>> rng = DiscreteAliasUrn(pv, domain=(10, 13), random_state=urng)
>>> rng.rvs()
12 # may vary
Метод также работает, когда вместо вектора вероятностей задана PMF.
В этом случае ограниченная (конечная) область также должна быть задана либо путём
передачи domain параметр явно или путем предоставления support
метод в объекте распределения:
>>> class Distribution:
... def __init__(self, c):
... self.c = c
... def pmf(self, x):
... return x**self.c
... def support(self):
... return (0, 10)
...
>>> dist = Distribution(2)
>>> rng = DiscreteAliasUrn(dist, random_state=urng)
>>> rng.rvs()
10 # may vary
>>> import matplotlib.pyplot as plt
>>> from scipy.stats.sampling import DiscreteAliasUrn
>>> class Distribution:
... def __init__(self, c):
... self.c = c
... def pmf(self, x):
... return x**self.c
... def support(self):
... return (0, 10)
...
>>> dist = Distribution(2)
>>> urng = np.random.default_rng()
>>> rng = DiscreteAliasUrn(dist, random_state=urng)
>>> rvs = rng.rvs(1000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> x = np.arange(1, 11)
>>> fx = dist.pmf(x)
>>> fx = fx / fx.sum()
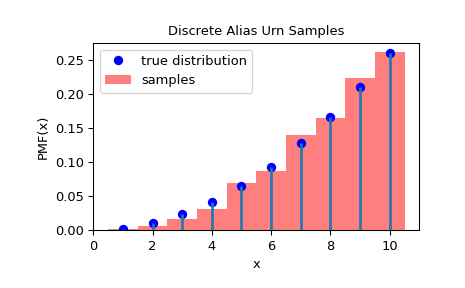
>>> ax.plot(x, fx, 'bo', label='true distribution')
>>> ax.vlines(x, 0, fx, lw=2)
>>> ax.hist(rvs, bins=np.r_[x, 11]-0.5, density=True, alpha=0.5, color='r',
... label='samples')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('PMF(x)')
>>> ax.set_title('Discrete Alias Urn Samples')
>>> plt.legend()
>>> plt.show()
Примечание
Поскольку DiscreteAliasUrn ожидает PMF с сигнатурой
def pmf(self, x: float) -> float, сначала векторизует PMF с помощью np.vectorize и затем вычисляет её во всех точках области определения. Но если PMF уже векторизован, гораздо быстрее просто вычислить её в каждой точке области определения и передать полученный PV вместе с областью. Например, pmf методы дискретных распределений SciPy векторизованы, и PV можно получить, выполнив:
>>> from scipy.stats import binom
>>> from scipy.stats.sampling import DiscreteAliasUrn
>>> dist = binom(10, 0.2) # distribution object
>>> domain = dist.support() # the domain of your distribution
>>> x = np.arange(domain[0], domain[1] + 1)
>>> pv = dist.pmf(x)
>>> rng = DiscreteAliasUrn(pv, domain=domain)
Здесь требуется домен для перемещения распределения.
Производительность может незначительно зависеть от размера используемой таблицы, который можно изменить, передав urn_factor параметр.
>>> # use a table twice the length of PV.
>>> urn_factor = 2
>>> rng = DiscreteAliasUrn(pv, urn_factor=urn_factor, random_state=urng)
>>> rng.rvs()
2 # may vary
Примечание
Рекомендуется держать этот параметр ниже 2.
Пожалуйста, смотрите [1] и [2] для получения дополнительных сведений об этом методе.