numpy.random.Generator.normal#

метод

random.Generator.нормальный(loc=0.0, scale=1.0, размер=None)#

Генерация случайных выборок из нормального (гауссовского) распределения.

Функция плотности вероятности нормального распределения, впервые выведенная Де Муавром и 200 лет спустя независимо Гауссом и Лапласом [2], часто называется кривой колокола из-за её характерной формы (см. пример ниже).

Нормальное распределение часто встречается в природе. Например, оно описывает часто встречающееся распределение выборок, на которые влияет большое количество крошечных случайных возмущений, каждое со своим уникальным распределением [2].

Параметры:

locfloat или array_like из float: Среднее («центр») распределения.
scalefloat или array_like из float: Стандартное отклонение (разброс или «ширина») распределения. Должно быть неотрицательным.
размерint или кортеж ints, опционально: Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если loc и scale оба являются скалярами. В противном случае, np.broadcast(loc, scale).size выбираются образцы.

Возвращает:

выходndarray или скаляр: Выбранные образцы из параметризованного нормального распределения.

Смотрите также

scipy.stats.norm: функция плотности вероятности, распределение или интегральная функция распределения и т.д.

Примечания

Функция плотности вероятности для нормального распределения равна

\[p(x) = \frac{1}{\sqrt{ 2 \pi \sigma^2 }} e^{ - \frac{ (x - \mu)^2 } {2 \sigma^2} },\]

где \(\mu\) является средним значением и \(\sigma\) стандартное отклонение. Квадрат стандартного отклонения, \(\sigma^2\), называется дисперсией.

Функция достигает пика при среднем значении, и её «разброс» увеличивается со стандартным отклонением (функция достигает 0.607 от максимума при \(x + \sigma\) и \(x - \sigma\) [2]). Это подразумевает, что normal с большей вероятностью возвращает выборки, лежащие близко к среднему значению, а не те, что далеко.

Ссылки

[1]

Википедия, "Нормальное распределение", https://en.wikipedia.org/wiki/Normal_distribution

[2] (1,2,3)

P. R. Peebles Jr., "Центральная предельная теорема" в "Вероятность, случайные величины и принципы случайных сигналов", 4-е изд., 2001, стр. 51, 51, 125.

Примеры

Извлечь выборки из распределения:

>>> mu, sigma = 0, 0.1 # mean and standard deviation
>>> rng = np.random.default_rng()
>>> s = rng.normal(mu, sigma, 1000)

Проверьте среднее значение и стандартное отклонение:

>>> abs(mu - np.mean(s))
0.0  # may vary

>>> abs(sigma - np.std(s, ddof=1))
0.0  # may vary

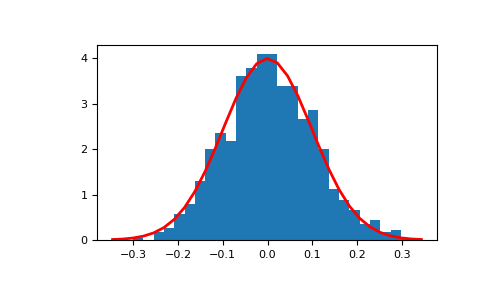
Отображение гистограммы выборок вместе с функцией плотности вероятности:

>>> import matplotlib.pyplot as plt
>>> count, bins, _ = plt.hist(s, 30, density=True)
>>> plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
...                np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
...          linewidth=2, color='r')
>>> plt.show()

../../../_images/numpy-random-Generator-normal-1_00_00.png

Двухмерный массив 2x4 выборок из нормального распределения со средним 3 и стандартным отклонением 2.5:

>>> rng = np.random.default_rng()
>>> rng.normal(3, 2.5, size=(2, 4))
array([[-4.49401501,  4.00950034, -1.81814867,  7.29718677],   # random
       [ 0.39924804,  4.68456316,  4.99394529,  4.84057254]])  # random