Тест Флигнера-Киллена на равенство дисперсий#
В [1], влияние витамина C на рост зубов морских свинок было исследовано. В контрольном исследовании 60 субъектов были разделены на группы малой дозы, средней дозы и большой дозы, которые получали ежедневные дозы 0.5, 1.0 и 2.0 мг витамина C соответственно. Через 42 дня был измерен рост зубов.
The small_dose, medium_dose, и large_dose Массивы ниже содержат измерения роста зубов трех групп в микронах.
import numpy as np
small_dose = np.array([
4.2, 11.5, 7.3, 5.8, 6.4, 10, 11.2, 11.2, 5.2, 7,
15.2, 21.5, 17.6, 9.7, 14.5, 10, 8.2, 9.4, 16.5, 9.7
])
medium_dose = np.array([
16.5, 16.5, 15.2, 17.3, 22.5, 17.3, 13.6, 14.5, 18.8, 15.5,
19.7, 23.3, 23.6, 26.4, 20, 25.2, 25.8, 21.2, 14.5, 27.3
])
large_dose = np.array([
23.6, 18.5, 33.9, 25.5, 26.4, 32.5, 26.7, 21.5, 23.3, 29.5,
25.5, 26.4, 22.4, 24.5, 24.8, 30.9, 26.4, 27.3, 29.4, 23
])
Статистика Флигнера-Киллена (scipy.stats.fligner) чувствителен к различиям в дисперсиях между выборками.
from scipy import stats
res = stats.fligner(small_dose, medium_dose, large_dose)
res.statistic
np.float64(1.3878943408857916)
Значение статистики стремится быть высоким, когда есть большая разница в дисперсиях.
Мы можем проверить неравенство дисперсий между группами, сравнив наблюдаемое значение статистики с нулевым распределением: распределением значений статистики, полученных при нулевой гипотезе о том, что дисперсии генеральных совокупностей трех групп равны.
Для этого теста нулевое распределение следует распределение хи-квадрат как показано ниже.
import matplotlib.pyplot as plt
k = 3 # number of samples
dist = dist = stats.chi2(df=k-1)
val = np.linspace(0, 8, 100)
pdf = dist.pdf(val)
fig, ax = plt.subplots(figsize=(8, 5))
def plot(ax): # we'll reuse this
ax.plot(val, pdf, color='C0')
ax.set_title("Fligner Test Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
ax.set_xlim(0, 8)
ax.set_ylim(0, 0.5)
plot(ax)
plt.show()
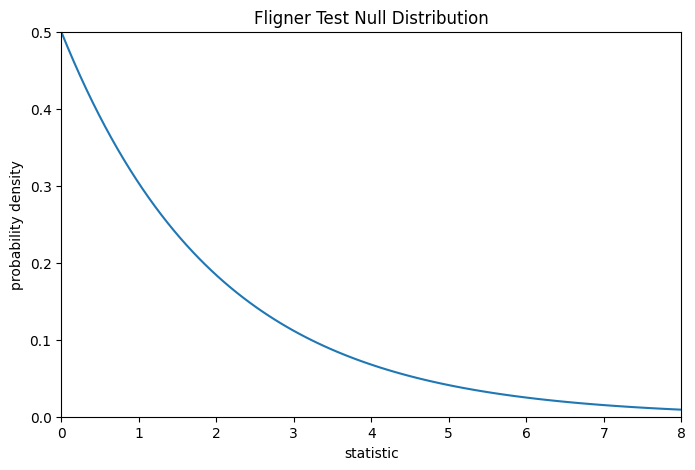
Сравнение количественно выражается через p-значение: доля значений в нулевом распределении, больших или равных наблюдаемому значению статистики.
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
pvalue = dist.sf(res.statistic)
annotation = (f'p-value={pvalue:.4f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (1.5, 0.22), (2.25, 0.3), arrowprops=props)
i = val >= res.statistic
ax.fill_between(val[i], y1=0, y2=pdf[i], color='C0')
plt.show()
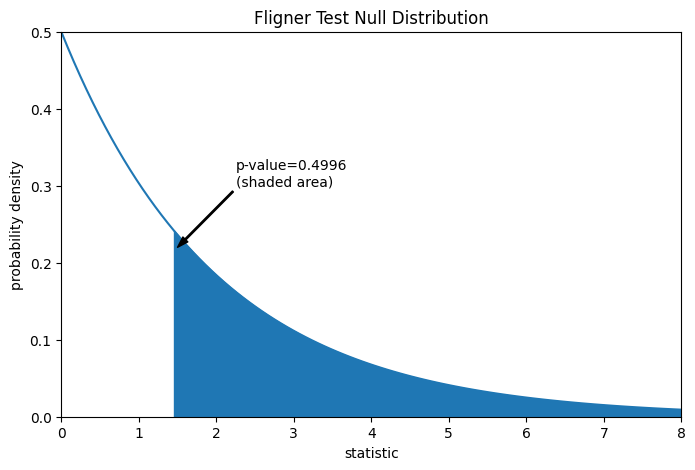
res.pvalue
np.float64(0.49960016501182125)
Если p-значение "маленькое" - то есть, если существует низкая вероятность выборки данных из распределений с одинаковыми дисперсиями, которые дают такое экстремальное значение статистики - это может быть принято как свидетельство против нулевой гипотезы в пользу альтернативной: дисперсии групп не равны. Обратите внимание, что:
Обратное неверно; то есть тест не используется для предоставления доказательств в пользу нулевой гипотезы.
Порог для значений, которые будут считаться «малыми», — это выбор, который следует сделать до анализа данных [2] с учетом рисков как ложноположительных (ошибочное отклонение нулевой гипотезы), так и ложноотрицательных (неспособность отклонить ложную нулевую гипотезу).
Маленькие p-значения не являются доказательством большой эффект; скорее, они могут только предоставить доказательства «значимого» эффекта, означающего, что они маловероятны при нулевой гипотезе.
Обратите внимание, что распределение хи-квадрат даёт асимптотическое приближение нулевого распределения. Для малых выборок может быть более уместно выполнить перестановочный тест: при нулевой гипотезе, что все три выборки были взяты из одной и той же совокупности, каждое измерение с равной вероятностью могло быть наблюдаемо в любой из трёх выборок. Поэтому мы можем сформировать рандомизированное нулевое распределение, вычисляя статистику при многих случайно сгенерированных разбиениях наблюдений на три выборки.
def statistic(*samples):
return stats.fligner(*samples).statistic
ref = stats.permutation_test(
(small_dose, medium_dose, large_dose), statistic,
permutation_type='independent', alternative='greater'
)
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
bins = np.linspace(0, 8, 25)
ax.hist(
ref.null_distribution, bins=bins, density=True, facecolor="C1"
)
ax.legend(['asymptotic approximation\n(many observations)',
'randomized null distribution'])
plot(ax)
plt.show()
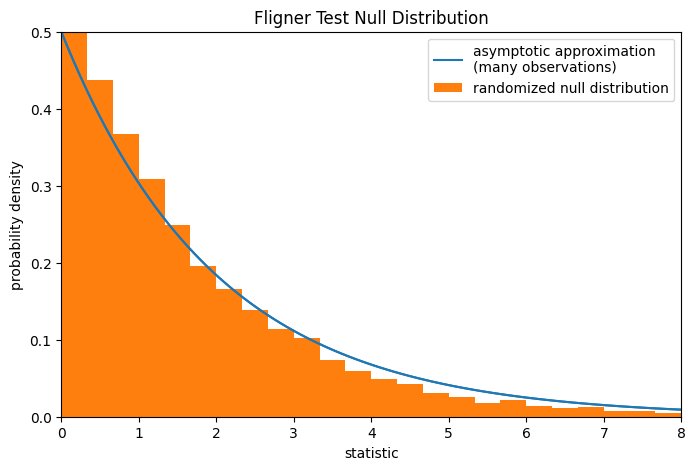
ref.pvalue # randomized test p-value
np.float64(0.4379)
Обратите внимание, что существует значительное расхождение между p-значением, рассчитанным здесь, и асимптотической аппроксимацией, возвращаемой scipy.stats.fligner выше.
Статистические выводы, которые можно строго сделать из перестановочного теста, ограничены; тем не менее, они могут быть предпочтительным подходом во многих обстоятельствах [3].