Тест Левена на равенство дисперсий#
Тест Левена scipy.stats.levene проверяет нулевую гипотезу о том, что все
входные выборки взяты из популяций с равными дисперсиями. Тест Левена является альтернативой тесту Бартлетта scipy.stats.bartlett в случае, когда
имеются значительные отклонения от нормальности.
В [1], влияние витамина C на рост зубов морских свинок было исследовано. В контрольном исследовании 60 субъектов были разделены на группы малой дозы, средней дозы и большой дозы, которые получали ежедневные дозы 0.5, 1.0 и 2.0 мг витамина C соответственно. Через 42 дня был измерен рост зубов.
The small_dose, medium_dose, и large_dose Массивы ниже содержат измерения роста зубов трех групп в микронах.
import numpy as np
small_dose = np.array([
4.2, 11.5, 7.3, 5.8, 6.4, 10, 11.2, 11.2, 5.2, 7,
15.2, 21.5, 17.6, 9.7, 14.5, 10, 8.2, 9.4, 16.5, 9.7
])
medium_dose = np.array([
16.5, 16.5, 15.2, 17.3, 22.5, 17.3, 13.6, 14.5, 18.8, 15.5,
19.7, 23.3, 23.6, 26.4, 20, 25.2, 25.8, 21.2, 14.5, 27.3
])
large_dose = np.array([
23.6, 18.5, 33.9, 25.5, 26.4, 32.5, 26.7, 21.5, 23.3, 29.5,
25.5, 26.4, 22.4, 24.5, 24.8, 30.9, 26.4, 27.3, 29.4, 23
])
The scipy.stats.levene статистика чувствительна к различиям в
дисперсиях между выборками.
from scipy import stats
res = stats.levene(small_dose, medium_dose, large_dose)
res.statistic
np.float64(0.6457341109631506)
Значение статистики стремится быть высоким, когда есть большая разница в дисперсиях.
Мы можем проверить неравенство дисперсий между группами, сравнив наблюдаемое значение статистики с нулевым распределением: распределением значений статистики, полученных при нулевой гипотезе о том, что дисперсии генеральных совокупностей трех групп равны.
Для этого теста нулевое распределение следует F-распределению, как показано ниже.
import matplotlib.pyplot as plt
k, n = 3, 60 # number of samples, total number of observations
dist = stats.f(dfn=k-1, dfd=n-k)
val = np.linspace(0, 5, 100)
pdf = dist.pdf(val)
fig, ax = plt.subplots(figsize=(8, 5))
def plot(ax): # we'll reuse this
ax.plot(val, pdf, color='C0')
ax.set_title("Levene Test Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
ax.set_xlim(0, 5)
ax.set_ylim(0, 1)
plot(ax)
plt.show()
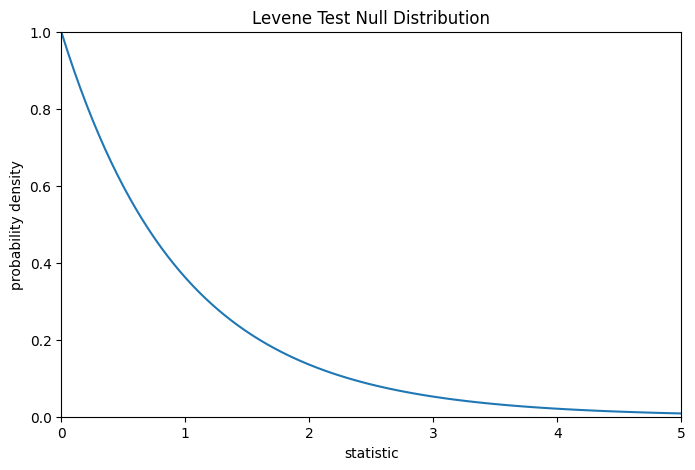
Сравнение количественно выражается через p-значение: доля значений в нулевом распределении, больших или равных наблюдаемому значению статистики.
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
pvalue = dist.sf(res.statistic)
annotation = (f'p-value={pvalue:.3f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (1.5, 0.22), (2.25, 0.3), arrowprops=props)
i = val >= res.statistic
ax.fill_between(val[i], y1=0, y2=pdf[i], color='C0')
plt.show()
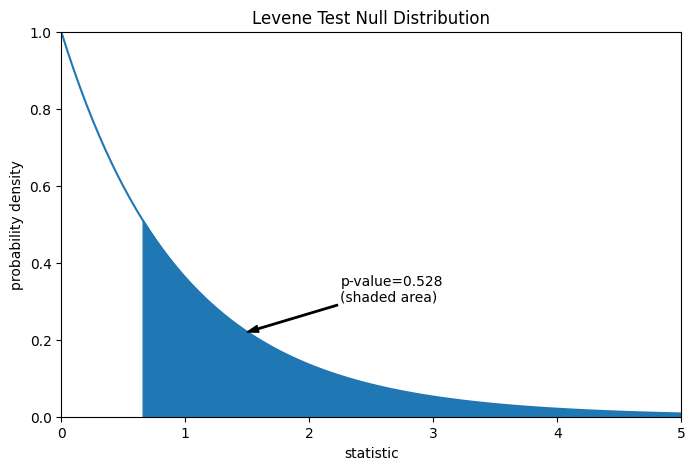
res.pvalue
np.float64(0.5280694573759905)
Если p-значение "маленькое" - то есть, если существует низкая вероятность выборки данных из распределений с одинаковыми дисперсиями, которые дают такое экстремальное значение статистики - это может быть принято как свидетельство против нулевой гипотезы в пользу альтернативной: дисперсии групп не равны. Обратите внимание, что:
Обратное неверно; то есть тест не используется для предоставления доказательств в пользу нулевой гипотезы.
Порог для значений, которые будут считаться «малыми», — это выбор, который следует сделать до анализа данных [2] с учетом рисков как ложноположительных (ошибочное отклонение нулевой гипотезы), так и ложноотрицательных (неспособность отклонить ложную нулевую гипотезу).
Маленькие p-значения не являются доказательством большой эффект; скорее, они могут только предоставить доказательства «значимого» эффекта, означающего, что они маловероятны при нулевой гипотезе.
Обратите внимание, что распределение Фишера даёт асимптотическое приближение нулевого распределения. Для малых выборок может быть более уместным выполнить перестановочный тест: согласно нулевой гипотезе о том, что все три выборки были взяты из одной и той же совокупности, каждое измерение с равной вероятностью могло быть наблюдаемо в любой из трёх выборок. Следовательно, мы можем сформировать рандомизированное нулевое распределение, вычисляя статистику для многих случайно сгенерированных разбиений наблюдений на три выборки.
def statistic(*samples):
return stats.levene(*samples).statistic
ref = stats.permutation_test(
(small_dose, medium_dose, large_dose), statistic,
permutation_type='independent', alternative='greater'
)
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
bins = np.linspace(0, 5, 25)
ax.hist(
ref.null_distribution, bins=bins, density=True, facecolor="C1"
)
ax.legend(['asymptotic approximation\n(many observations)',
'randomized null distribution'])
plot(ax)
plt.show()
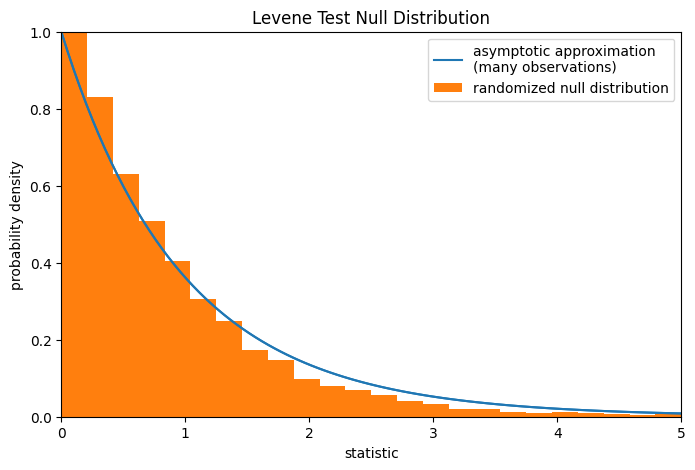
ref.pvalue # randomized test p-value
np.float64(0.4645)
Обратите внимание, что существует значительное расхождение между p-значением, рассчитанным здесь, и асимптотической аппроксимацией, возвращаемой scipy.stats.levene выше.
Статистические выводы, которые можно строго сделать из перестановочного теста, ограничены; тем не менее, они могут быть предпочтительным подходом во многих обстоятельствах [3].