Оценка плотности ядра

Распространённой задачей в статистике является оценка функции плотности вероятности (PDF) случайной величины по набору выборочных данных. Эта задача называется оценкой плотности. Наиболее известный инструмент для этого — гистограмма. Гистограмма полезна для визуализации (в основном потому, что её понимают все), но не очень эффективно использует доступные данные. Оценка плотности ядра (KDE) — более эффективный инструмент для той же задачи. scipy.stats.gaussian_kde оценщик может использоваться для оценки PDF одномерных, а также многомерных данных. Он работает лучше всего, если данные унимодальны.

Одномерное оценивание

Мы начинаем с минимального количества данных, чтобы увидеть, как scipy.stats.gaussian_kde работает и что делают различные варианты выбора полосы пропускания. Данные, выбранные из PDF, показаны синими черточками внизу рисунка (это называется rug plot):

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt

>>> x1 = np.array([-7, -5, 1, 4, 5], dtype=np.float64)
>>> kde1 = stats.gaussian_kde(x1)
>>> kde2 = stats.gaussian_kde(x1, bw_method='silverman')

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)

>>> ax.plot(x1, np.zeros(x1.shape), 'b+', ms=20)  # rug plot
>>> x_eval = np.linspace(-10, 10, num=200)
>>> ax.plot(x_eval, kde1(x_eval), 'k-', label="Scott's Rule")
>>> ax.plot(x_eval, kde2(x_eval), 'r-', label="Silverman's Rule")

>>> plt.show()

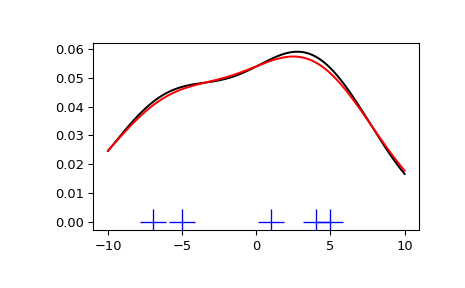
Мы видим, что между правилом Скотта и правилом Сильвермана очень мало разницы, и что выбор ширины полосы с ограниченным количеством данных, вероятно, немного слишком широк. Мы можем определить свою собственную функцию ширины полосы, чтобы получить менее сглаженный результат.

>>> def my_kde_bandwidth(obj, fac=1./5):
...     """We use Scott's Rule, multiplied by a constant factor."""
...     return np.power(obj.n, -1./(obj.d+4)) * fac

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)

>>> ax.plot(x1, np.zeros(x1.shape), 'b+', ms=20)  # rug plot
>>> kde3 = stats.gaussian_kde(x1, bw_method=my_kde_bandwidth)
>>> ax.plot(x_eval, kde3(x_eval), 'g-', label="With smaller BW")

>>> plt.show()

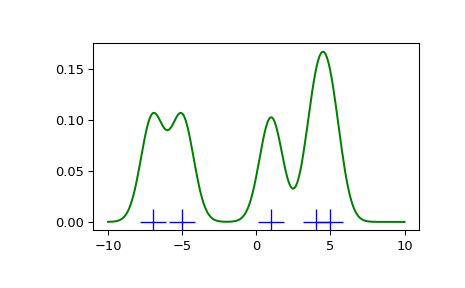
Мы видим, что если установить ширину полосы очень узкой, полученная оценка для функции плотности вероятности (PDF) представляет собой просто сумму гауссиан вокруг каждой точки данных.

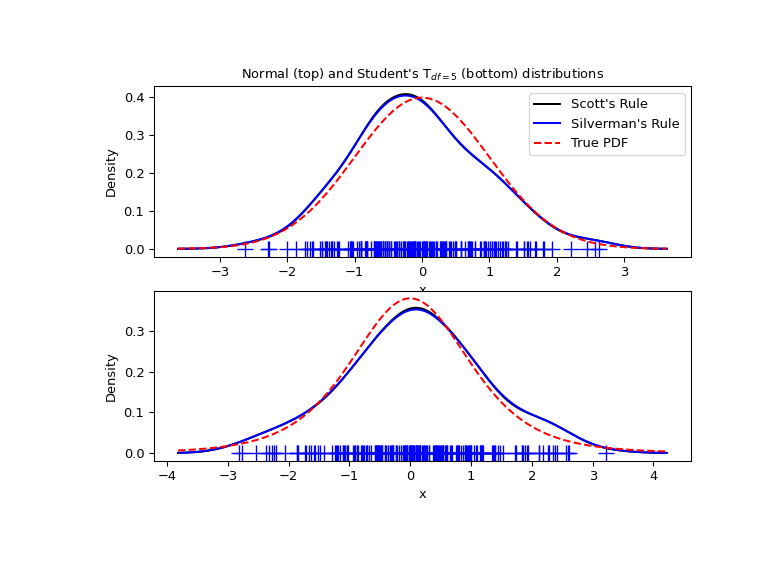
Теперь рассмотрим более реалистичный пример и посмотрим на разницу между двумя доступными правилами выбора ширины окна. Известно, что эти правила хорошо работают для (близких к) нормальным распределениям, но даже для унимодальных распределений, которые довольно сильно отличаются от нормального, они работают достаточно хорошо. В качестве ненормального распределения возьмем распределение Стьюдента с 5 степенями свободы.

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats


rng = np.random.default_rng()
x1 = rng.normal(size=200)  # random data, normal distribution
xs = np.linspace(x1.min()-1, x1.max()+1, 200)

kde1 = stats.gaussian_kde(x1)
kde2 = stats.gaussian_kde(x1, bw_method='silverman')

fig = plt.figure(figsize=(8, 6))

ax1 = fig.add_subplot(211)
ax1.plot(x1, np.zeros(x1.shape), 'b+', ms=12)  # rug plot
ax1.plot(xs, kde1(xs), 'k-', label="Scott's Rule")
ax1.plot(xs, kde2(xs), 'b-', label="Silverman's Rule")
ax1.plot(xs, stats.norm.pdf(xs), 'r--', label="True PDF")

ax1.set_xlabel('x')
ax1.set_ylabel('Density')
ax1.set_title("Normal (top) and Student's T$_{df=5}$ (bottom) distributions")
ax1.legend(loc=1)

x2 = stats.t.rvs(5, size=200, random_state=rng)  # random data, T distribution
xs = np.linspace(x2.min() - 1, x2.max() + 1, 200)

kde3 = stats.gaussian_kde(x2)
kde4 = stats.gaussian_kde(x2, bw_method='silverman')

ax2 = fig.add_subplot(212)
ax2.plot(x2, np.zeros(x2.shape), 'b+', ms=12)  # rug plot
ax2.plot(xs, kde3(xs), 'k-', label="Scott's Rule")
ax2.plot(xs, kde4(xs), 'b-', label="Silverman's Rule")
ax2.plot(xs, stats.t.pdf(xs, 5), 'r--', label="True PDF")

ax2.set_xlabel('x')
ax2.set_ylabel('Density')

plt.show()

Теперь рассмотрим бимодальное распределение с одной более широкой и одной более узкой гауссовой особенностью. Ожидается, что это будет более сложная плотность для аппроксимации из-за различных полос пропускания, необходимых для точного разрешения каждой особенности.

>>> from functools import partial

>>> loc1, scale1, size1 = (-2, 1, 175)
>>> loc2, scale2, size2 = (2, 0.2, 50)
>>> x2 = np.concatenate([np.random.normal(loc=loc1, scale=scale1, size=size1),
...                      np.random.normal(loc=loc2, scale=scale2, size=size2)])

>>> x_eval = np.linspace(x2.min() - 1, x2.max() + 1, 500)

>>> kde = stats.gaussian_kde(x2)
>>> kde2 = stats.gaussian_kde(x2, bw_method='silverman')
>>> kde3 = stats.gaussian_kde(x2, bw_method=partial(my_kde_bandwidth, fac=0.2))
>>> kde4 = stats.gaussian_kde(x2, bw_method=partial(my_kde_bandwidth, fac=0.5))

>>> pdf = stats.norm.pdf
>>> bimodal_pdf = pdf(x_eval, loc=loc1, scale=scale1) * float(size1) / x2.size + \
...               pdf(x_eval, loc=loc2, scale=scale2) * float(size2) / x2.size

>>> fig = plt.figure(figsize=(8, 6))
>>> ax = fig.add_subplot(111)

>>> ax.plot(x2, np.zeros(x2.shape), 'b+', ms=12)
>>> ax.plot(x_eval, kde(x_eval), 'k-', label="Scott's Rule")
>>> ax.plot(x_eval, kde2(x_eval), 'b-', label="Silverman's Rule")
>>> ax.plot(x_eval, kde3(x_eval), 'g-', label="Scott * 0.2")
>>> ax.plot(x_eval, kde4(x_eval), 'c-', label="Scott * 0.5")
>>> ax.plot(x_eval, bimodal_pdf, 'r--', label="Actual PDF")

>>> ax.set_xlim([x_eval.min(), x_eval.max()])
>>> ax.legend(loc=2)
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('Density')
>>> plt.show()

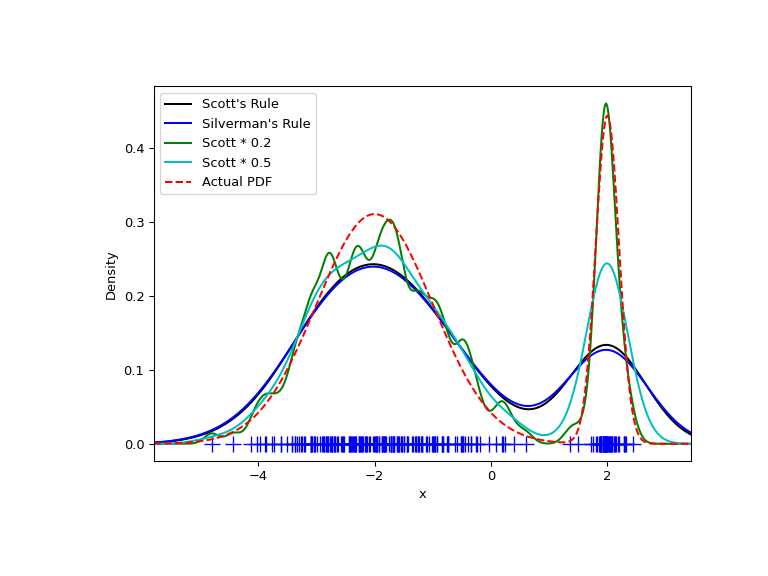
Как и ожидалось, KDE не так близок к истинной PDF, как нам хотелось бы, из-за различного характерного размера двух особенностей бимодального распределения. Уменьшив полосу пропускания по умолчанию вдвое (Scott * 0.5), мы можем добиться несколько лучших результатов, в то время как использование полосы пропускания в 5 раз меньше, чем по умолчанию, недостаточно сглаживает. Однако в данном случае нам действительно нужна неоднородная (адаптивная) полоса пропускания.

Многомерное оценивание

С scipy.stats.gaussian_kde мы можем выполнить многомерную, а также одномерную оценку. Мы демонстрируем двумерный случай. Сначала мы генерируем некоторые случайные данные с моделью, в которой две переменные коррелированы.

>>> def measure(n):
...     """Measurement model, return two coupled measurements."""
...     m1 = np.random.normal(size=n)
...     m2 = np.random.normal(scale=0.5, size=n)
...     return m1+m2, m1-m2

>>> m1, m2 = measure(2000)
>>> xmin = m1.min()
>>> xmax = m1.max()
>>> ymin = m2.min()
>>> ymax = m2.max()

Затем применяем KDE к данным:

>>> X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
>>> positions = np.vstack([X.ravel(), Y.ravel()])
>>> values = np.vstack([m1, m2])
>>> kernel = stats.gaussian_kde(values)
>>> Z = np.reshape(kernel.evaluate(positions).T, X.shape)

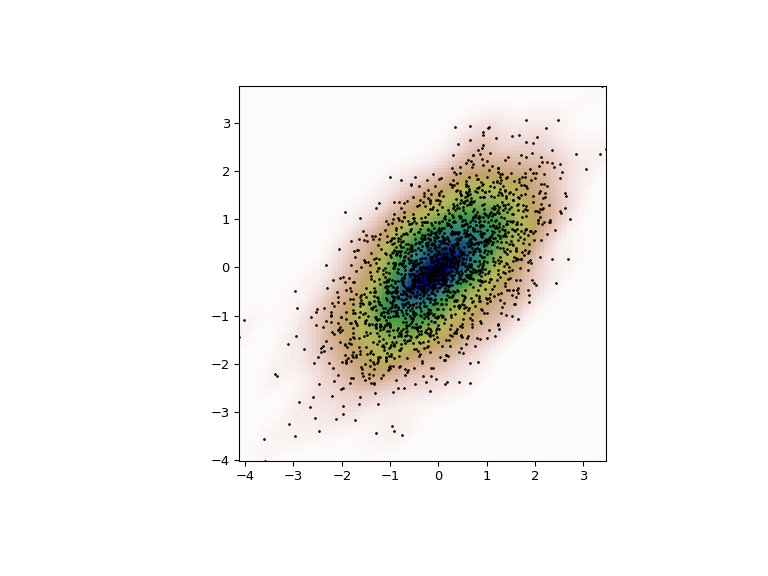
Наконец, мы строим оценённое двумерное распределение как цветовую карту и наносим отдельные точки данных сверху.

>>> fig = plt.figure(figsize=(8, 6))
>>> ax = fig.add_subplot(111)

>>> ax.imshow(np.rot90(Z), cmap=plt.cm.gist_earth_r,
...           extent=[xmin, xmax, ymin, ymax])
>>> ax.plot(m1, m2, 'k.', markersize=2)

>>> ax.set_xlim([xmin, xmax])
>>> ax.set_ylim([ymin, ymax])

>>> plt.show()