Simple Ratio-of-Uniforms (SROU)#
Требуется: PDF, площадь под PDF, если отличается от 1
Опционально: мода, CDF в моде
Скорость:
Настройка: быстро
Выборка: медленно
SROU основан на методе отношения равномерных распределений, который использует универсальные неравенства для построения (универсального) ограничивающего прямоугольника. Он работает для T-вогнутых распределений с T(x) = -1/sqrt(x).
>>> import numpy as np
>>> from scipy.stats.sampling import SimpleRatioUniforms
Предположим, у нас есть нормальное распределение:
>>> class StdNorm:
... def pdf(self, x):
... return np.exp(-0.5 * x**2)
Обратите внимание, что PDF не интегрируется в 1. Мы можем либо передать точную площадь под PDF при инициализации генератора, либо верхнюю границу точной площади под PDF. Также рекомендуется передать моду распределения для ускорения настройки:
>>> urng = np.random.default_rng()
>>> dist = StdNorm()
>>> rng = SimpleRatioUniforms(dist, mode=0,
... pdf_area=np.sqrt(2*np.pi),
... random_state=urng)
Теперь мы можем использовать rvs метод для генерации выборок из распределения:
>>> rvs = rng.rvs(10)
Если доступна CDF в моде, её можно установить для улучшения производительности rvs:
>>> from scipy.stats import norm
>>> rng = SimpleRatioUniforms(dist, mode=0,
... pdf_area=np.sqrt(2*np.pi),
... cdf_at_mode=norm.cdf(0),
... random_state=urng)
>>> rvs = rng.rvs(1000)
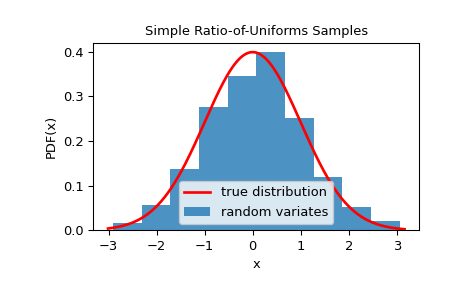
Мы можем проверить, что выборки взяты из заданного распределения, визуализировав его гистограмму:
>>> from scipy.stats.sampling import SimpleRatioUniforms
>>> from scipy.stats import norm
>>> import matplotlib.pyplot as plt
>>> class StdNorm:
... def pdf(self, x):
... return np.exp(-0.5 * x**2)
...
>>> urng = np.random.default_rng()
>>> dist = StdNorm()
>>> rng = SimpleRatioUniforms(dist, mode=0,
... pdf_area=np.sqrt(2*np.pi),
... cdf_at_mode=norm.cdf(0),
... random_state=urng)
>>> rvs = rng.rvs(1000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000)
>>> fx = 1/np.sqrt(2*np.pi) * dist.pdf(x)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> ax.hist(rvs, bins=10, density=True, alpha=0.8, label='random variates')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('PDF(x)')
>>> ax.set_title('Simple Ratio-of-Uniforms Samples')
>>> ax.legend()
>>> plt.show()
Основное преимущество метода — быстрая настройка. Это может быть полезно, если нужно
повторно генерировать небольшие или умеренные выборки распределения с
различными параметрами формы. В такой ситуации шаг настройки
sampling.NumericalInverseHermite или sampling.NumericalInversePolynomial приведет к плохой производительности. В качестве примера предположим, что мы хотим сгенерировать 100 выборок для гамма-распределения с 1000 различными параметрами формы, заданными np.arange(1.5, 5, 1000).
>>> import math
>>> class GammaDist:
... def __init__(self, p):
... self.p = p
... def pdf(self, x):
... return x**(self.p-1) * np.exp(-x)
...
>>> urng = np.random.default_rng()
>>> p = np.arange(1.5, 5, 1000)
>>> res = np.empty((1000, 100))
>>> for i in range(1000):
... dist = GammaDist(p[i])
... rng = SimpleRatioUniforms(dist, mode=p[i]-1,
... pdf_area=math.gamma(p[i]),
... random_state=urng)
... with np.testing.suppress_warnings() as sup:
... sup.filter(RuntimeWarning, "invalid value encountered in double_scalars")
... sup.filter(RuntimeWarning, "overflow encountered in exp")
... res[i] = rng.rvs(100)
См. [1], [2], и [3] для получения дополнительной информации.