Интерполяция Эрмита на основе инверсии CDF (HINV)#
Требуется: CDF
Опционально: PDF, dPDF
Скорость:
Настройка: (очень) медленная
Сэмплирование: (очень) быстрое
HINV — это вариант численной инверсии, где обратная CDF аппроксимируется с помощью интерполяции Эрмита, т.е. интервал [0,1] разбивается на несколько интервалов, и в каждом интервале обратная CDF аппроксимируется полиномами, построенными на основе значений CDF и PDF на границах интервалов. Это позволяет улучшить точность, разбивая конкретный интервал без пересчётов в незатронутых интервалах. Реализованы три типа сплайнов: линейная, кубическая и квинтическая интерполяция. Для линейной интерполяции требуется только CDF. Кубическая интерполяция также требует PDF, а квинтическая — PDF и её производную.
Эти сплайны должны быть вычислены на этапе настройки. Однако это работает только для распределений с ограниченной областью; для распределений с неограниченной областью хвосты обрезаются так, что вероятность для хвостовых областей мала по сравнению с заданным u-разрешением.
Метод не является точным, так как он производит только случайные величины аппроксимированного
распределения. Тем не менее, максимальная численная ошибка в "u-направлении" (т.е.
|U - CDF(X)| где X является приблизительным процентилем, соответствующим
квантилю U т.е. X = approx_ppf(U)) может быть установлено на требуемое разрешение (в пределах машинной точности). Обратите внимание, что очень маленькие значения u-разрешения возможны, но могут увеличить стоимость шага настройки.
NumericalInverseHermite аппроксимирует обратную функцию непрерывного
статистического распределения CDF с помощью сплайна Эрмита. Порядок
сплайна Эрмита может быть задан передачей порядок параметр.
Как описано в [1], он начинается с вычисления PDF и
CDF распределения на сетке квантилей x в пределах носителя распределения.
Он использует результаты для подгонки сплайна Эрмита H такой, что
H(p) == x, где p является массивом процентилей, соответствующих
квантилям x. Поэтому сплайн аппроксимирует обратную
функцию CDF распределения с машинной точностью на перцентилях p, но обычно сплайн будет менее точным в средних точках между процентилями:
p_mid = (p[:-1] + p[1:])/2
так что сетка квантилей уточняется по мере необходимости для уменьшения максимальной "u-ошибки":
u_error = np.max(np.abs(dist.cdf(H(p_mid)) - p_mid))
ниже указанного допуска u_resolutionУточнение останавливается, когда достигнута требуемая допустимая погрешность или когда количество интервалов сетки после следующего уточнения может превысить максимально допустимое количество интервалов (100000).
>>> import numpy as np
>>> from scipy.stats.sampling import NumericalInverseHermite
>>> from scipy.stats import norm, genexpon
>>> from scipy.special import ndtr
Чтобы создать генератор для выборки из стандартного нормального распределения, сделайте:
>>> class StandardNormal:
... def pdf(self, x):
... return 1/np.sqrt(2*np.pi) * np.exp(-x**2 / 2)
... def cdf(self, x):
... return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInverseHermite(dist, random_state=urng)
The NumericalInverseHermite имеет метод, который аппроксимирует PPF
распределения.
>>> rng = NumericalInverseHermite(dist)
>>> p = np.linspace(0.01, 0.99, 99) # percentiles from 1% to 99%
>>> np.allclose(rng.ppf(p), norm.ppf(p))
True
В зависимости от реализации метода случайной выборки распределения, сгенерированные случайные величины могут быть почти идентичными при одинаковом случайном состоянии.
>>> dist = genexpon(9, 16, 3)
>>> rng = NumericalInverseHermite(dist)
>>> # `seed` ensures identical random streams are used by each `rvs` method
>>> seed = 500072020
>>> rvs1 = dist.rvs(size=100, random_state=np.random.default_rng(seed))
>>> rvs2 = rng.rvs(size=100, random_state=np.random.default_rng(seed))
>>> np.allclose(rvs1, rvs2)
True
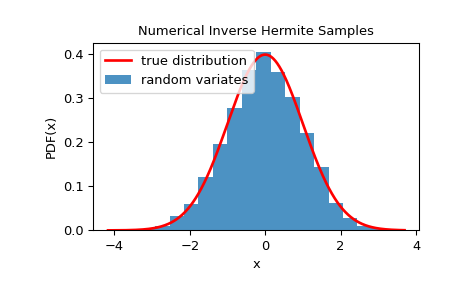
Чтобы проверить, что случайные величины близко следуют заданному распределению, можно посмотреть на его гистограмму:
>>> import matplotlib.pyplot as plt
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInverseHermite(dist, random_state=urng)
>>> rvs = rng.rvs(10000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000)
>>> fx = norm.pdf(x)
>>> plt.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates')
>>> plt.xlabel('x')
>>> plt.ylabel('PDF(x)')
>>> plt.title('Numerical Inverse Hermite Samples')
>>> plt.legend()
>>> plt.show()
Учитывая производную PDF по переменной (т.е. x), мы можем использовать
интерполяцию Эрмита пятой степени для аппроксимации PPF, передавая порядок
параметр:
>>> class StandardNormal:
... def pdf(self, x):
... return 1/np.sqrt(2*np.pi) * np.exp(-x**2 / 2)
... def dpdf(self, x):
... return -1/np.sqrt(2*np.pi) * x * np.exp(-x**2 / 2)
... def cdf(self, x):
... return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInverseHermite(dist, order=5, random_state=urng)
Более высокие порядки приводят к меньшему количеству интервалов:
>>> rng3 = NumericalInverseHermite(dist, order=3)
>>> rng5 = NumericalInverseHermite(dist, order=5)
>>> rng3.intervals, rng5.intervals
(3000, 522)
Ошибку u можно оценить, вызвав u_error метод. Он запускает небольшое моделирование Монте-Карло для оценки u-ошибки. По умолчанию используется 100 000 образцов. Это можно изменить, передав sample_size аргумент:
>>> rng1 = NumericalInverseHermite(dist, u_resolution=1e-10)
>>> rng1.u_error(sample_size=1000000) # uses one million samples
UError(max_error=9.53167544892608e-11, mean_absolute_error=2.2450136432146864e-11)
Это возвращает namedtuple, который содержит максимальную u-ошибку и среднюю абсолютную u-ошибку.
U-ошибку можно уменьшить, снизив u-разрешение (максимально допустимая u-ошибка):
>>> rng2 = NumericalInverseHermite(dist, u_resolution=1e-13)
>>> rng2.u_error(sample_size=1000000)
UError(max_error=9.32027892364129e-14, mean_absolute_error=1.5194172675685075e-14)
Обратите внимание, что это происходит за счет времени вычислений из-за увеличенного времени настройки и количества интервалов.
>>> rng1.intervals
1022
>>> rng2.intervals
5687
>>> from timeit import timeit
>>> f = lambda: NumericalInverseHermite(dist, u_resolution=1e-10)
>>> timeit(f, number=1)
0.017409582000254886 # may vary
>>> f = lambda: NumericalInverseHermite(dist, u_resolution=1e-13)
>>> timeit(f, number=1)
0.08671202100003939 # may vary
См. [1] и [2] для получения дополнительных сведений об этом методе.