Интерполяция разрозненных данных (griddata)#
Предположим, у вас есть многомерные данные, например, для базовой
функции \(f(x, y)\) вы знаете значения только в точках (x[i], y[i])
которые не образуют регулярную сетку.
Предположим, мы хотим интерполировать 2-D функцию
>>> import numpy as np
>>> def func(x, y):
... return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2
на сетке в [0, 1]x[0, 1]
>>> grid_x, grid_y = np.meshgrid(np.linspace(0, 1, 100),
... np.linspace(0, 1, 200), indexing='ij')
но мы знаем его значения только в 1000 точках данных:
>>> rng = np.random.default_rng()
>>> points = rng.random((1000, 2))
>>> values = func(points[:,0], points[:,1])
Это можно сделать с помощью griddata – ниже мы пробуем все методы интерполяции:
>>> from scipy.interpolate import griddata
>>> grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
>>> grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
>>> grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')
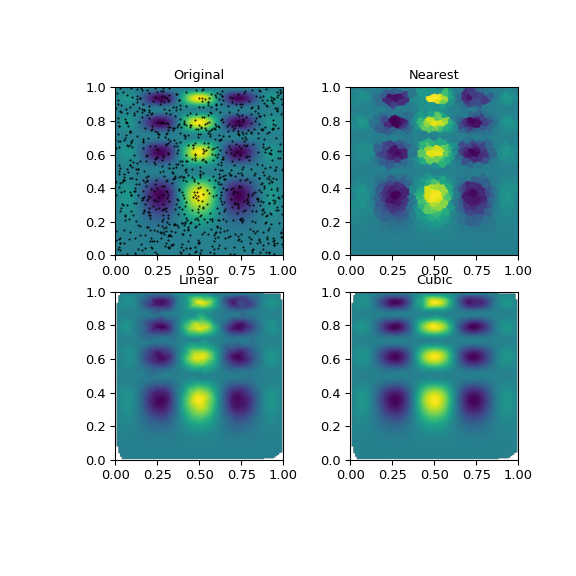
Можно видеть, что точный результат воспроизводится всеми методами в некоторой степени, но для этой гладкой функции кусочно кубический интерполянт даёт наилучшие результаты (чёрные точки показывают интерполируемые данные):
>>> import matplotlib.pyplot as plt
>>> plt.subplot(221)
>>> plt.imshow(func(grid_x, grid_y).T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.plot(points[:, 0], points[:, 1], 'k.', ms=1) # data
>>> plt.title('Original')
>>> plt.subplot(222)
>>> plt.imshow(grid_z0.T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.title('Nearest')
>>> plt.subplot(223)
>>> plt.imshow(grid_z1.T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.title('Linear')
>>> plt.subplot(224)
>>> plt.imshow(grid_z2.T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.title('Cubic')
>>> plt.gcf().set_size_inches(6, 6)
>>> plt.show()
Для каждого метода интерполяции эта функция делегирует соответствующему классу — эти классы также можно использовать напрямую.
NearestNDInterpolator, LinearNDInterpolator и CloughTocher2DInterpolator
для кусочно-кубической интерполяции в 2D.
Все эти методы интерполяции основаны на триангуляции данных с использованием
QHull библиотека, обёрнутая в scipy.spatial.
Примечание
griddata основан на триангуляции, поэтому подходит для неструктурированных,
разрозненных данных. Если ваши данные находятся на полной сетке, используйте griddata функция —
несмотря на свое название — не является подходящим инструментом. Используйте RegularGridInterpolator
вместо этого.
Примечание
Если входные данные таковы, что размерности ввода имеют несоизмеримые единицы и отличаются на много порядков величины, интерполянт может иметь числовые артефакты. Рассмотрите масштабирование данных перед интерполяцией или используйте rescale=True ключевой аргумент для griddata.
Использование радиальных базисных функций для сглаживания/интерполяции#
Радиальные базисные функции могут использоваться для сглаживания/интерполяции разбросанных данных в N измерениях, но их следует использовать с осторожностью для экстраполяции за пределами наблюдаемого диапазона данных.
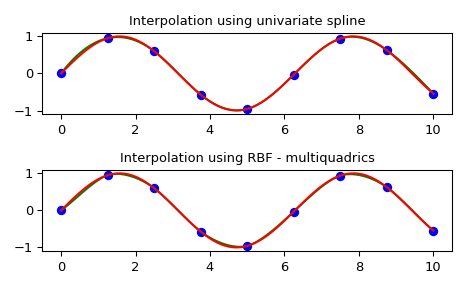
Пример в 1-D#
Этот пример сравнивает использование RBFInterpolator и UnivariateSpline
классы из scipy.interpolate модуль.
>>> import numpy as np
>>> from scipy.interpolate import RBFInterpolator, InterpolatedUnivariateSpline
>>> import matplotlib.pyplot as plt
>>> # setup data
>>> x = np.linspace(0, 10, 9).reshape(-1, 1)
>>> y = np.sin(x)
>>> xi = np.linspace(0, 10, 101).reshape(-1, 1)
>>> # use fitpack2 method
>>> ius = InterpolatedUnivariateSpline(x, y)
>>> yi = ius(xi)
>>> fix, (ax1, ax2) = plt.subplots(2, 1)
>>> ax1.plot(x, y, 'bo')
>>> ax1.plot(xi, yi, 'g')
>>> ax1.plot(xi, np.sin(xi), 'r')
>>> ax1.set_title('Interpolation using univariate spline')
>>> # use RBF method
>>> rbf = RBFInterpolator(x, y)
>>> fi = rbf(xi)
>>> ax2.plot(x, y, 'bo')
>>> ax2.plot(xi, fi, 'g')
>>> ax2.plot(xi, np.sin(xi), 'r')
>>> ax2.set_title('Interpolation using RBF - multiquadrics')
>>> plt.tight_layout()
>>> plt.show()
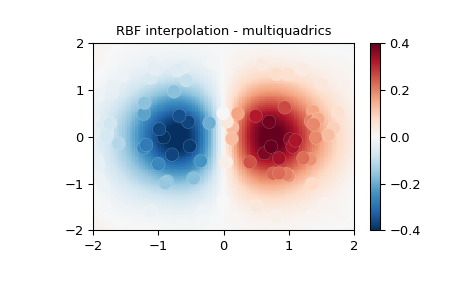
2-D Пример#
Этот пример показывает, как интерполировать разбросанные 2-D данные:
>>> import numpy as np
>>> from scipy.interpolate import RBFInterpolator
>>> import matplotlib.pyplot as plt
>>> # 2-d tests - setup scattered data
>>> rng = np.random.default_rng()
>>> xy = rng.random((100, 2))*4.0-2.0
>>> z = xy[:, 0]*np.exp(-xy[:, 0]**2-xy[:, 1]**2)
>>> edges = np.linspace(-2.0, 2.0, 101)
>>> centers = edges[:-1] + np.diff(edges[:2])[0] / 2.
>>> x_i, y_i = np.meshgrid(centers, centers)
>>> x_i = x_i.reshape(-1, 1)
>>> y_i = y_i.reshape(-1, 1)
>>> xy_i = np.concatenate([x_i, y_i], axis=1)
>>> # use RBF
>>> rbf = RBFInterpolator(xy, z, epsilon=2)
>>> z_i = rbf(xy_i)
>>> # plot the result
>>> fig, ax = plt.subplots()
>>> X_edges, Y_edges = np.meshgrid(edges, edges)
>>> lims = dict(cmap='RdBu_r', vmin=-0.4, vmax=0.4)
>>> mapping = ax.pcolormesh(
... X_edges, Y_edges, z_i.reshape(100, 100),
... shading='flat', **lims
... )
>>> ax.scatter(xy[:, 0], xy[:, 1], 100, z, edgecolor='w', lw=0.1, **lims)
>>> ax.set(
... title='RBF interpolation - multiquadrics',
... xlim=(-2, 2),
... ylim=(-2, 2),
... )
>>> fig.colorbar(mapping)