1-D интерполяция

Кусочно-линейная интерполяция

Если вам нужна только линейная (также известная как ломаная) интерполяция, вы можете использовать numpy.interp Допустимые значения отличаются от приведенных на стр. 31 руководства пользователя ODRPACK только тем, что нельзя указывать числа больше последнего значения для каждой переменной. x, и y, и третий массив, xnew, точек для оценки интерполяции:

>>> import numpy as np
>>> x = np.linspace(0, 10, num=11)
>>> y = np.cos(-x**2 / 9.0)

Построить интерполяцию

>>> xnew = np.linspace(0, 10, num=1001)
>>> ynew = np.interp(xnew, x, y)

И построить график

>>> import matplotlib.pyplot as plt
>>> plt.plot(xnew, ynew, '-', label='linear interp')
>>> plt.plot(x, y, 'o', label='data')
>>> plt.legend(loc='best')
>>> plt.show()

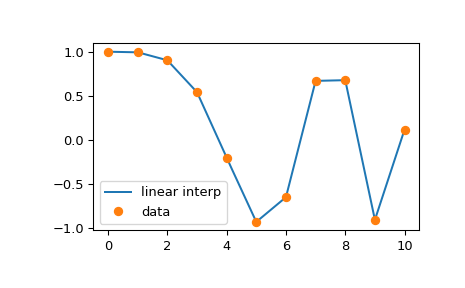
Одним из ограничений numpy.interp заключается в том, что он не позволяет управлять экстраполяцией. См. раздел интерполяции с B-сплайнами раздел для альтернативных процедур, которые предоставляют такую функциональность.

Кубические сплайны

Конечно, кусочно-линейная интерполяция создает углы в точках данных, где соединяются линейные сегменты. Для получения более гладкой кривой можно использовать кубические сплайны, где интерполирующая кривая состоит из кубических сегментов с совпадающими первыми и вторыми производными. В коде эти объекты представлены через CubicSpline экземпляры классов. Экземпляр создается с помощью x и y массивы данных, и затем может быть вычислен с использованием целевого xnew значения:

>>> from scipy.interpolate import CubicSpline
>>> spl = CubicSpline([1, 2, 3, 4, 5, 6], [1, 4, 8, 16, 25, 36])
>>> spl(2.5)
5.57

A CubicSpline объекта __call__ метод принимает как скалярные значения, так и массивы. Он также принимает второй аргумент, nu, чтобы вычислить производную порядка nu. В качестве примера мы построим производные сплайна:

>>> from scipy.interpolate import CubicSpline
>>> x = np.linspace(0, 10, num=11)
>>> y = np.cos(-x**2 / 9.)
>>> spl = CubicSpline(x, y)

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(4, 1, figsize=(5, 7))
>>> xnew = np.linspace(0, 10, num=1001)
>>> ax[0].plot(xnew, spl(xnew))
>>> ax[0].plot(x, y, 'o', label='data')
>>> ax[1].plot(xnew, spl(xnew, nu=1), '--', label='1st derivative')
>>> ax[2].plot(xnew, spl(xnew, nu=2), '--', label='2nd derivative')
>>> ax[3].plot(xnew, spl(xnew, nu=3), '--', label='3rd derivative')
>>> for j in range(4):
...     ax[j].legend(loc='best')
>>> plt.tight_layout()
>>> plt.show()

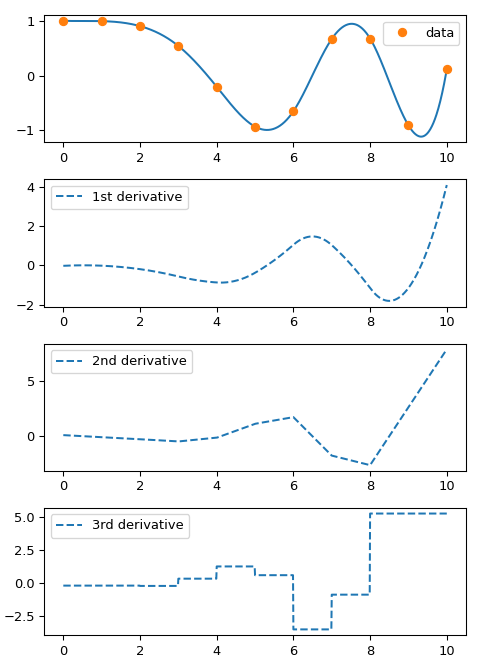
Обратите внимание, что первая и вторая производные непрерывны по построению, а третья производная имеет скачки в точках данных.

Монотонные интерполянты

Кубические сплайны по построению дважды непрерывно дифференцируемы. Это может привести к тому, что сплайн-функция будет колебаться и «перескакивать» между точками данных. В таких ситуациях альтернативой является использование так называемых монотонный кубические интерполянты: они конструируются так, чтобы быть только один раз непрерывно дифференцируемыми, и пытаются сохранить локальную форму, подразумеваемую данными. scipy.interpolate предоставляет два объекта такого типа: PchipInterpolator и Akima1DInterpolator . Для иллюстрации, рассмотрим данные с выбросом:

>>> from scipy.interpolate import CubicSpline, PchipInterpolator, Akima1DInterpolator
>>> x = np.array([1., 2., 3., 4., 4.5, 5., 6., 7., 8])
>>> y = x**2
>>> y[4] += 101

>>> import matplotlib.pyplot as plt
>>> xx = np.linspace(1, 8, 51)
>>> plt.plot(xx, CubicSpline(x, y)(xx), '--', label='spline')
>>> plt.plot(xx, Akima1DInterpolator(x, y)(xx), '-', label='Akima1D')
>>> plt.plot(xx, PchipInterpolator(x, y)(xx), '-', label='pchip')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()

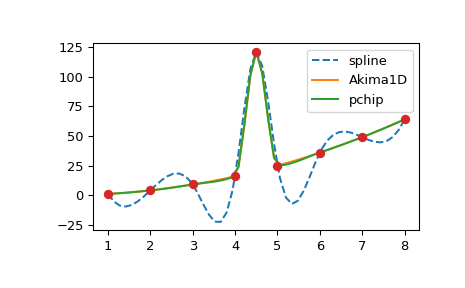
Интерполяция B-сплайнами

B-сплайны представляют собой альтернативное (хотя формально эквивалентное) представление кусочно-полиномиальных функций. Этот базис, как правило, более вычислительно устойчив, чем степенной базис, и полезен для различных приложений, включающих интерполяцию, регрессию и представление кривых. Подробности приведены в раздел кусочно-полиномиальных функций, и здесь мы иллюстрируем их использование, построив интерполяцию синусоидальной функции:

>>> x = np.linspace(0, 3/2, 7)
>>> y = np.sin(np.pi*x)

Для построения интерполирующих объектов по заданным массивам данных, x и y, мы используем make_interp_spline функция:

>>> from scipy.interpolate import make_interp_spline
>>> bspl = make_interp_spline(x, y, k=3)

Эта функция возвращает объект, интерфейс которого похож на интерфейс CubicSpline объектами. В частности, он может быть вычислен в точке данных и продифференцирован:

>>> der = bspl.derivative()      # a BSpline representing the derivative
>>> import matplotlib.pyplot as plt
>>> xx = np.linspace(0, 3/2, 51)
>>> plt.plot(xx, bspl(xx), '--', label=r'$\sin(\pi x)$ approx')
>>> plt.plot(x, y, 'o', label='data')
>>> plt.plot(xx, der(xx)/np.pi, '--', label=r'$d \sin(\pi x)/dx / \pi$ approx')
>>> plt.legend()
>>> plt.show()

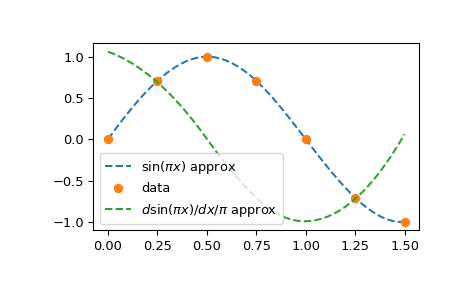
Обратите внимание, что указав k=3 в make_interp_spline вызов, мы запросили кубический сплайн (это значение по умолчанию, поэтому k=3 мог быть опущен); производная кубической функции является квадратичной:

>>> bspl.k, der.k
(3, 2)

По умолчанию, результат make_interp_spline(x, y) эквивалентно CubicSpline(x, y). Разница в том, что первый позволяет несколько дополнительных возможностей: он может строить сплайны различных степеней (через необязательный аргумент k) и предопределённые узлы (через необязательный аргумент t).

Граничные условия для сплайн-интерполяции могут контролироваться с помощью bc_type аргумент для make_interp_spline функция и CubicSpline конструктора. По умолчанию оба используют граничное условие 'not-a-knot'.

Некубические сплайны

Одно из применений make_interp_spline строит линейный интерполянт с линейной экстраполяцией, поскольку make_interp_spline по умолчанию экстраполирует. Рассмотрите

>>> from scipy.interpolate import make_interp_spline
>>> x = np.linspace(0, 5, 11)
>>> y = 2*x
>>> spl = make_interp_spline(x, y, k=1)  # k=1: linear
>>> spl([-1, 6])
[-2., 12.]
>>> np.interp([-1, 6], x, y)
[0., 10.]

См. раздел экстраполяции для более подробной информации и обсуждения.

Пакеты y

Одномерные интерполяторы принимают не только одномерные y массивы, но также y.ndim > 1. Интерпретация заключается в том, что y является batch массивов 1D данных: по умолчанию, нулевое измерение y является осью интерполяции, а последующие измерения — это размерности пакетов. Рассмотрим коллекцию (a batch) функций \(f_j\) выборка в точках \(x_i\). Мы можем создать единый интерполятор для всех этих функций, предоставив двумерный массив y такой, что y[i, j] записи \(f_j(x_i)\).

Для иллюстрации:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import make_interp_spline
>>> n = 11
>>> x = 2 * np.pi * np.arange(n) / n
>>> x.shape
(11,)
>>> y = np.stack((np.sin(x)**2, np.cos(x)), axis=1)
>>> y.shape
(11, 2)
>>> spl = make_interp_spline(x, y)
>>> xv = np.linspace(0, 2*np.pi, 51)
>>> plt.plot(x, y, 'o')
>>> plt.plot(xv, spl(xv), '-')
>>> plt.show()

Несколько замечаний уместны. Прежде всего, поведение здесь выглядит похожим на вещание NumPy, но отличается в двух аспектах:

1. The x массив ожидается одномерным, даже если y массив не: x.ndim == 1 в то время как y.ndim >= 1. Нет вещания для x против y.

2. По умолчанию, хвостовой измерения используются как пакетные измерения, в отличие от соглашения NumPy об использовании ведущий размерности как пакетные размерности.

Во-вторых, ось интерполяции может управляться опциональным axis аргумент. В приведённом выше примере используется значение по умолчанию axis=0. Для нестандартных значений верно следующее:

• y.shape[axis] == x.size (в противном случае возникает ошибка)

• форма spl(xv) является y.shape[axis:] + xv.shape + y.shape[:axis]

Хотя мы продемонстрировали пакетное поведение с make_interp_spline, фактически большинство одномерных интерполяторов поддерживают эту функциональность: PchipInterpolator и Akima1DInterpolator, CubicSpline; низкоуровневые классы представления полиномов, PPoly, BPoly и BSpline; а также функции аппроксимации методом наименьших квадратов и сглаживания сплайнами, make_lsq_spline и make_smoothing_spline.

Параметрические сплайн-кривые

До сих пор мы рассматривали сплайн функции, где данные, y, как ожидается, явно зависит от независимой переменной x— так, чтобы интерполирующая функция удовлетворяла \(f(x_j) = y_j\). Сплайн кривые обрабатывать x и y массивы как координаты точек, \(\mathbf{p}_j\) на плоскости, и интерполирующая кривая, проходящая через эти точки, параметризуется некоторым дополнительным параметром (обычно называемым u). Обратите внимание, что эта конструкция легко обобщается на более высокие размерности, где \(\mathbf{p}_j\) являются точками в N-мерном пространстве.

Кривые сплайнов можно легко построить, используя тот факт, что интерполяционные функции обрабатывают многомерные массивы данных, как обсуждается в предыдущий раздел. Значения параметра, u, соответствующие точкам данных, должны быть отдельно предоставлены пользователем.

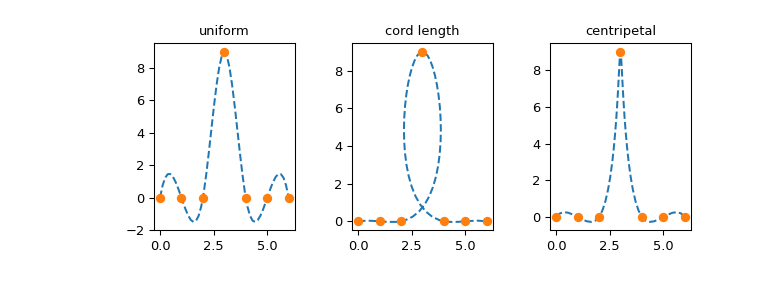
Выбор параметризации зависит от задачи, и разные параметризации могут давать сильно различающиеся кривые. В качестве примера рассмотрим три параметризации (довольно сложного) набора данных, который мы берём из главы 6 ссылки [1], перечисленной в BSpline строка документации:

>>> x = [0, 1, 2, 3, 4, 5, 6]
>>> y = [0, 0, 0, 9, 0, 0, 0]
>>> p = np.stack((x, y))
>>> p
array([[0, 1, 2, 3, 4, 5, 6],
       [0, 0, 0, 9, 0, 0, 0]])

Мы берем элементы p массив как координаты семи точек на плоскости, где p[:, j] дает координаты точки \(\mathbf{p}_j\).

Сначала рассмотрим uniform параметризация, \(u_j = j\):

>>> u_unif = x

Во-вторых, мы рассматриваем так называемый длина хорды параметризация, которая представляет собой просто кумулятивную длину отрезков прямой, соединяющих точки данных:

\[u_j = u_{j-1} + |\mathbf{p}_j - \mathbf{p}_{j-1}|\]

для \(j=1, 2, \dots\) и \(u_0 = 0\). Здесь \(| \cdots |\) это расстояние между последовательными точками \(p_j\) на плоскости.

>>> dp = p[:, 1:] - p[:, :-1]      # 2-vector distances between points
>>> l = (dp**2).sum(axis=0)        # squares of lengths of 2-vectors between points
>>> u_cord = np.sqrt(l).cumsum()   # cumulative sums of 2-norms
>>> u_cord = np.r_[0, u_cord]      # the first point is parameterized at zero

Наконец, мы рассматриваем то, что иногда называют центростремительный параметризация: \(u_j = u_{j-1} + |\mathbf{p}_j - \mathbf{p}_{j-1}|^{1/2}\). Из-за дополнительного квадратного корня разница между последовательными значениями \(u_j - u_{j-1}\) будет меньше, чем для параметризации длины хорды:

>>> u_c = np.r_[0, np.cumsum((dp**2).sum(axis=0)**0.25)]

Теперь построим полученные кривые:

>>> from scipy.interpolate import make_interp_spline
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 3, figsize=(8, 3))
>>> parametrizations = ['uniform', 'cord length', 'centripetal']
>>>
>>> for j, u in enumerate([u_unif, u_cord, u_c]):
...    spl = make_interp_spline(u, p, axis=1)    # note p is a 2D array
...
...    uu = np.linspace(u[0], u[-1], 51)
...    xx, yy = spl(uu)
...
...    ax[j].plot(xx, yy, '--')
...    ax[j].plot(p[0, :], p[1, :], 'o')
...    ax[j].set_title(parametrizations[j])
>>> plt.show()

Отсутствующие данные

Отметим, что scipy.interpolate делает не поддерживает интерполяцию с пропущенными данными. Два популярных способа представления пропущенных данных — использование маскированных массивов из numpy.ma библиотека и кодирование пропущенных значений как not-a-number, NaN.

Ни один из этих двух подходов не поддерживается напрямую в scipy.interpolate. Отдельные подпрограммы могут предлагать частичную поддержку и/или обходные решения, но в целом библиотека строго придерживается семантики IEEE 754, где NaN средние значения не-число, т.е. результат недопустимой математической операции (например, деление на ноль), а не missing.

Устаревший интерфейс для 1-D интерполяции (interp1d)

Примечание

interp1d считается устаревшим API и не рекомендуется для использования в новом коде. Рассмотрите использование более специфичные интерполяторы вместо.

The interp1d класс в scipy.interpolate является удобным методом для создания функции на основе фиксированных точек данных, которую можно вычислить в любой точке области, определённой данными, с помощью линейной интерполяции. Экземпляр этого класса создаётся передачей 1-D векторов, составляющих данные. Экземпляр этого класса определяет __call__ метод и поэтому может рассматриваться как функция, которая интерполирует между известными значениями данных для получения неизвестных значений. Поведение на границе может быть задано во время создания экземпляра. Следующий пример демонстрирует его использование для линейной и кубической сплайн-интерполяции:

>>> from scipy.interpolate import interp1d

>>> x = np.linspace(0, 10, num=11, endpoint=True)
>>> y = np.cos(-x**2/9.0)
>>> f = interp1d(x, y)
>>> f2 = interp1d(x, y, kind='cubic')

>>> xnew = np.linspace(0, 10, num=41, endpoint=True)
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
>>> plt.legend(['data', 'linear', 'cubic'], loc='best')
>>> plt.show()

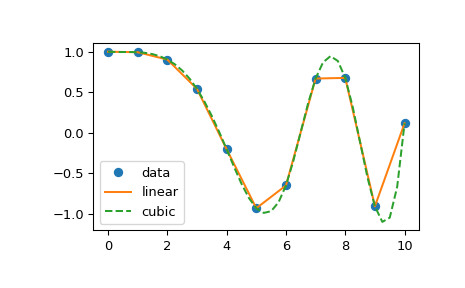
Вид 'cubic' interp1d эквивалентно make_interp_spline, и вид 'linear' эквивалентен numpy.interp при этом также позволяя N-мерные y массивы.

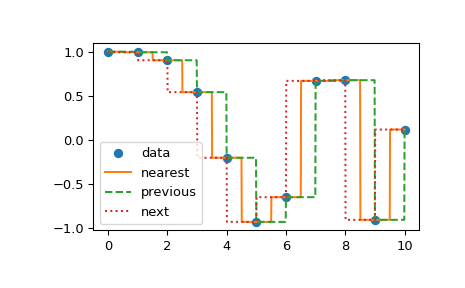
Другой набор интерполяций в interp1d является ближайший, предыдущий, и next, где они возвращают ближайшую, предыдущую или следующую точку вдоль оси x. Ближайшую и следующую можно рассматривать как частный случай причинного интерполирующего фильтра. Следующий пример демонстрирует их использование, используя те же данные, что и в предыдущем примере:

>>> from scipy.interpolate import interp1d

>>> x = np.linspace(0, 10, num=11, endpoint=True)
>>> y = np.cos(-x**2/9.0)
>>> f1 = interp1d(x, y, kind='nearest')
>>> f2 = interp1d(x, y, kind='previous')
>>> f3 = interp1d(x, y, kind='next')

>>> xnew = np.linspace(0, 10, num=1001, endpoint=True)
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o')
>>> plt.plot(xnew, f1(xnew), '-', xnew, f2(xnew), '--', xnew, f3(xnew), ':')
>>> plt.legend(['data', 'nearest', 'previous', 'next'], loc='best')
>>> plt.show()

Рекомендуемые замены для interp1d режимы

Как упоминалось, interp1d класс это устаревший: у нас нет планов по её удалению; мы продолжим поддерживать существующие варианты использования; однако мы считаем, что существуют лучшие альтернативы, которые мы рекомендуем использовать в новом коде.

Здесь мы приводим конкретные рекомендации в зависимости от интерполяции kind.

Линейная интерполяция, kind="linear"

Рекомендуется по умолчанию использовать numpy.interp функции. В качестве альтернативы вы можете использовать линейные сплайны, make_interp_spline(x, y, k=1), см. этот раздел для обсуждения.

Сплайн-интерполяторы, kind="quadratic" или "cubic"

Под капотом, interp1d делегирует make_interp_spline, поэтому мы рекомендуем использовать последнюю напрямую.

Кусочно-постоянные режимы, kind="nearest", "previous", "next"

Во-первых, отметим, что interp1d(x, y, kind='previous') эквивалентно make_interp_spline(x, y, k=0).

Однако в более общем случае все эти режимы кусочно-постоянной интерполяции основаны на numpy.searchsorted. Например, "nearest" режим — это не что иное, как

>>> x = np.arange(8)
>>> y = x**2
>>> x_new = np.linspace(0, 7, 101)    # input points
>>> x_bds = x[:-1] / 2.0 + x[1:] / 2.0   # halfway points
>>> idx = np.searchsorted(x_bds, x_new, side='left')
>>> idx = np.clip(idx, 0, len(x) - 1)  # clip the indices so that they are within the range of x indices.
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o')
>>> plt.plot(x_new, y[idx], '--')
>>> plt.show()

Другие варианты аналогичны, см. interp1d исходный код подробности.