Вероятностные распределения#

SciPy имеет две инфраструктуры для работы с распределениями вероятностей. Это руководство предназначено для старой, которая имеет много предопределённых распределений; однако новая инфраструктура может использоваться с большинством из них и имеет много преимуществ. Для новой инфраструктуры см. Руководство по переходу для случайных величин.

Существует два общих класса распределений, которые были реализованы для инкапсуляции непрерывные случайные величины и дискретные случайные величины. Более 100 непрерывных случайных величин (НСВ) и 20 дискретных случайных величин были реализованы с использованием этих классов. Для математической справочной информации об отдельных распределениях, пожалуйста, см. Непрерывные статистические распределения и Дискретные статистические распределения.

Все статистические функции находятся в подпакете scipy.stats и довольно полный список этих функций и случайных величин также можно получить из строки документации для подпакета stats.

В обсуждении ниже мы в основном фокусируемся на непрерывных случайных величинах. Почти всё также применимо к дискретным переменным, но мы отмечаем некоторые различия здесь: Конкретные моменты для дискретных распределений.

В приведённых ниже примерах кода мы предполагаем, что scipy.stats пакет импортируется как

>>> from scipy import stats

и в некоторых случаях мы предполагаем, что отдельные объекты импортируются как

>>> from scipy.stats import norm

Все распределения

Получение помощи#

Прежде всего, все распределения сопровождаются вспомогательными функциями. Чтобы получить лишь основную информацию, мы выводим соответствующий docstring: print(stats.norm.__doc__).

Чтобы найти носитель, т.е. верхнюю и нижнюю границы распределения, вызовите:

>>> print('bounds of distribution lower: %s, upper: %s' % norm.support())
bounds of distribution lower: -inf, upper: inf

Мы можем перечислить все методы и свойства распределения с помощью dir(norm). Как оказалось, некоторые методы являются приватными, хотя они не названы как таковые (их имена не начинаются с подчеркивания), например veccdf, доступны только для внутренних вычислений (эти методы будут выдавать предупреждения при попытке их использования и будут удалены в какой-то момент).

Для получения вещественный основные методы, мы перечисляем методы замороженного распределения. (Мы объясняем значение замороженный распределение ниже).

>>> rv = norm()
>>> dir(rv)  # reformatted
['__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__',
 '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__',
 '__init__', '__le__', '__lt__', '__module__', '__ne__', '__new__',
 '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__',
 '__str__', '__subclasshook__', '__weakref__', 'a', 'args', 'b', 'cdf',
 'dist', 'entropy', 'expect', 'interval', 'isf', 'kwds', 'logcdf',
 'logpdf', 'logpmf', 'logsf', 'mean', 'median', 'moment', 'pdf', 'pmf',
 'ppf', 'random_state', 'rvs', 'sf', 'stats', 'std', 'var']

Наконец, мы можем получить список доступных распределений через интроспекцию:

>>> dist_continu = [d for d in dir(stats) if
...                 isinstance(getattr(stats, d), stats.rv_continuous)]
>>> dist_discrete = [d for d in dir(stats) if
...                  isinstance(getattr(stats, d), stats.rv_discrete)]
>>> print('number of continuous distributions: %d' % len(dist_continu))
number of continuous distributions: 109
>>> print('number of discrete distributions:   %d' % len(dist_discrete))
number of discrete distributions:   21

Общие методы#

Основные публичные методы для непрерывных случайных величин:

  • rvs: Случайные величины

  • pdf: Функция плотности вероятности

  • cdf: Функция распределения

  • sf: Функция выживания (1-CDF)

  • ppf: Функция процентной точки (обратная к CDF)

  • isf: Обратная функция выживания (обратная к SF)

  • stats: Возвращает среднее, дисперсию, (Фишера) асимметрию или (Фишера) эксцесс

  • moment: нецентральные моменты распределения

Возьмем нормальную случайную величину в качестве примера.

>>> norm.cdf(0)
0.5

Для вычисления cdf в нескольких точках, мы можем передать список или массив numpy.

>>> norm.cdf([-1., 0, 1])
array([ 0.15865525,  0.5,  0.84134475])
>>> import numpy as np
>>> norm.cdf(np.array([-1., 0, 1]))
array([ 0.15865525,  0.5,  0.84134475])

Таким образом, основные методы, такие как pdf, функция распределения, и так далее, векторизованы.

Также поддерживаются другие общеполезные методы:

>>> norm.mean(), norm.std(), norm.var()
(0.0, 1.0, 1.0)
>>> norm.stats(moments="mv")
(array(0.0), array(1.0))

Чтобы найти медиану распределения, можно использовать функцию процентилей ppf, который является обратным к cdf:

>>> norm.ppf(0.5)
0.0

Для генерации последовательности случайных величин используйте size ключевой аргумент:

>>> norm.rvs(size=3)
array([-0.35687759,  1.34347647, -0.11710531])   # random

Не думайте, что norm.rvs(5) генерирует 5 вариантов:

>>> norm.rvs(5)
5.471435163732493  # random

Здесь, 5 без ключевого слова интерпретируется как первый возможный аргумент ключевого слова, loc, который является первым из пары ключевых аргументов, принимаемых всеми непрерывными распределениями. Это подводит нас к теме следующего подраздела.

Генерация случайных чисел#

Генерация случайных чисел основана на генераторах из numpy.random пакет. В примерах выше конкретный поток случайных чисел не воспроизводим между запусками. Для достижения воспроизводимости вы можете явно seed генератор случайных чисел. В NumPy генератор является экземпляром numpy.random.Generator. Вот канонический способ создания генератора:

>>> from numpy.random import default_rng
>>> rng = default_rng()

А фиксация начального значения может быть выполнена так:

>>> # do NOT copy this value
>>> rng = default_rng(301439351238479871608357552876690613766)

Предупреждение

Не используйте это число или общие значения, такие как 0. Использование лишь небольшого набора сидов для инициализации больших пространств состояний означает, что существуют некоторые начальные состояния, которые невозможно достичь. Это создает некоторые смещения, если все используют такие значения. Хороший способ получить сид — использовать numpy.random.SeedSequence:

>>> from numpy.random import SeedSequence
>>> print(SeedSequence().entropy)
301439351238479871608357552876690613766  # random

The random_state параметр в распределениях принимает экземпляр numpy.random.Generator класс, или целое число, которое затем используется для инициализации внутреннего Generator объект:

>>> norm.rvs(size=5, random_state=rng)
array([ 0.47143516, -1.19097569,  1.43270697, -0.3126519 , -0.72058873])  # random

Для дополнительной информации см. Документация NumPy.

Чтобы узнать больше о генераторах случайных чисел, реализованных в SciPy, см. руководство по неоднородной выборке случайных чисел и руководство по квази Монте-Карло

Сдвиг и масштабирование#

Все непрерывные распределения принимают loc и scale как ключевые параметры для настройки положения и масштаба распределения, например, для стандартного нормального распределения положение — это среднее, а масштаб — стандартное отклонение.

>>> norm.stats(loc=3, scale=4, moments="mv")
(array(3.0), array(16.0))

Во многих случаях стандартизированное распределение для случайной величины X получается через преобразование (X - loc) / scale. Значения по умолчанию: loc = 0 и scale = 1.

Умное использование loc и scale может помочь модифицировать стандартные распределения многими способами. Чтобы проиллюстрировать масштабирование далее, cdf экспоненциально распределённой случайной величины со средним \(1/\lambda\) задается формулой

\[F(x) = 1 - \exp(-\lambda x)\]

Применяя правило масштабирования выше, можно увидеть, что взяв scale  = 1./lambda мы получаем правильный масштаб.

>>> from scipy.stats import expon
>>> expon.mean(scale=3.)
3.0

Примечание

Распределения, принимающие параметры формы, могут требовать большего, чем простое применение loc и/или scale для достижения желаемой формы. Например, распределение длин 2-D векторов при заданном постоянном векторе длины \(R\) возмущены независимыми N(0, \(\sigma^2\)) отклонения в каждом компоненте rice(\(R/\sigma\), scale= \(\sigma\)). Первый аргумент - это параметр формы, который нужно масштабировать вместе с \(x\).

Равномерное распределение также интересно:

>>> from scipy.stats import uniform
>>> uniform.cdf([0, 1, 2, 3, 4, 5], loc=1, scale=4)
array([ 0.  ,  0.  ,  0.25,  0.5 ,  0.75,  1.  ])

Наконец, вспомним из предыдущего абзаца, что у нас осталась проблема значения norm.rvs(5). Как оказалось, при вызове распределения таким образом, первый аргумент, т.е. 5, передается для установки loc параметр. Посмотрим:

>>> np.mean(norm.rvs(5, size=500))
5.0098355106969992  # random

Таким образом, чтобы объяснить вывод примера из предыдущего раздела: norm.rvs(5) генерирует одну нормально распределённую случайную величину со средним loc=5, из-за значения по умолчанию size=1.

Мы рекомендуем установить loc и scale параметры явно, передавая значения как ключевые слова, а не как аргументы. Повторение можно минимизировать при вызове более одного метода данного RV, используя технику Замораживание распределения, как объяснено ниже.

Параметры формы#

Хотя общую непрерывную случайную величину можно сдвигать и масштабировать с помощью loc и scale параметры, некоторые распределения требуют дополнительных параметров формы. Например, гамма-распределение с плотностью

\[\gamma(x, a) = \frac{\lambda (\lambda x)^{a-1}}{\Gamma(a)} e^{-\lambda x}\;,\]

требует параметр формы \(a\). Заметьте, что установка \(\lambda\) может быть получена установкой scale ключевое слово для \(1/\lambda\).

Давайте проверим количество и имя параметров формы гамма- распределения. (Мы знаем из вышесказанного, что их должно быть 1.)

>>> from scipy.stats import gamma
>>> gamma.numargs
1
>>> gamma.shapes
'a'

Теперь мы устанавливаем значение переменной формы равным 1, чтобы получить экспоненциальное распределение, чтобы легко сравнить, получаем ли мы ожидаемые результаты.

>>> gamma(1, scale=2.).stats(moments="mv")
(array(2.0), array(4.0))

Обратите внимание, что мы также можем указать параметры формы как ключевые слова:

>>> gamma(a=1, scale=2.).stats(moments="mv")
(array(2.0), array(4.0))

Замораживание распределения#

Передача loc и scale ключевые слова снова и снова могут стать довольно надоедливыми. Концепция замораживание случайная величина используется для решения таких задач.

>>> rv = gamma(1, scale=2.)

Используя rv нам больше не нужно включать параметры масштаба или формы. Таким образом, распределения можно использовать одним из двух способов: либо передавая все параметры распределения при каждом вызове метода (как мы делали ранее), либо замораживая параметры для экземпляра распределения. Давайте проверим это:

>>> rv.mean(), rv.std()
(2.0, 2.0)

Это действительно то, что мы должны получить.

Трансляция (Broadcasting)#

Основные методы pdf, и так далее, удовлетворяют обычным правилам трансляции numpy. Например, мы можем вычислить критические значения для верхнего хвоста t-распределения для различных вероятностей и степеней свободы.

>>> stats.t.isf([0.1, 0.05, 0.01], [[10], [11]])
array([[ 1.37218364,  1.81246112,  2.76376946],
       [ 1.36343032,  1.79588482,  2.71807918]])

Здесь первая строка содержит критические значения для 10 степеней свободы и вторая строка для 11 степеней свободы (с.с.). Таким образом, правила трансляции дают тот же результат вызова isf дважды:

>>> stats.t.isf([0.1, 0.05, 0.01], 10)
array([ 1.37218364,  1.81246112,  2.76376946])
>>> stats.t.isf([0.1, 0.05, 0.01], 11)
array([ 1.36343032,  1.79588482,  2.71807918])

Если массив с вероятностями, т.е., [0.1, 0.05, 0.01] и массив степеней свободы, т.е., [10, 11, 12], имеют одинаковую форму массива, тогда используется поэлементное сопоставление. Например, мы можем получить 10% хвост для 10 степеней свободы, 5% хвост для 11 степеней свободы и 1% хвост для 12 степеней свободы, вызвав

>>> stats.t.isf([0.1, 0.05, 0.01], [10, 11, 12])
array([ 1.37218364,  1.79588482,  2.68099799])

Конкретные моменты для дискретных распределений#

Дискретные распределения в основном имеют те же базовые методы, что и непрерывные распределения. Однако pdf заменяется функцией вероятности массы pmf, методы оценки, такие как fit, недоступны, и scale не является допустимым ключевым параметром. Параметр расположения, ключевое слово loc, всё ещё может использоваться для сдвига распределения.

Вычисление функции распределения требует особого внимания. В случае непрерывного распределения, кумулятивная функция распределения, в большинстве стандартных случаев, строго монотонно возрастает в границах (a,b) и, следовательно, имеет уникальную обратную функцию. Однако функция распределения дискретного распределения является ступенчатой функцией, поэтому обратная функция распределения, т.е., функция процентной точки, требует другого определения:

ppf(q) = min{x : cdf(x) >= q, x integer}

Для дополнительной информации см. документацию здесь.

Мы можем рассмотреть гипергеометрическое распределение в качестве примера

>>> from scipy.stats import hypergeom
>>> [M, n, N] = [20, 7, 12]

Если мы используем функцию распределения в некоторых целых точках, а затем вычисляем обратную функцию распределения в этих значениях, мы получаем исходные целые числа обратно, например

>>> x = np.arange(4) * 2
>>> x
array([0, 2, 4, 6])
>>> prb = hypergeom.cdf(x, M, n, N)
>>> prb
array([  1.03199174e-04,   5.21155831e-02,   6.08359133e-01,
         9.89783282e-01])
>>> hypergeom.ppf(prb, M, n, N)
array([ 0.,  2.,  4.,  6.])

Если использовать значения, не находящиеся в точках излома ступенчатой функции cdf, мы получаем следующее большее целое число:

>>> hypergeom.ppf(prb + 1e-8, M, n, N)
array([ 1.,  3.,  5.,  7.])
>>> hypergeom.ppf(prb - 1e-8, M, n, N)
array([ 0.,  2.,  4.,  6.])

Подгонка распределений#

Основные дополнительные методы незамороженного распределения связаны с оценкой параметров распределения:

  • fit: оценка максимального правдоподобия параметров распределения, включая местоположение

    и масштаб

  • fit_loc_scale: оценка местоположения и масштаба при заданных параметрах формы

  • nnlf: функция отрицательного логарифма правдоподобия

  • expect: вычислить математическое ожидание функции относительно pdf или pmf

Проблемы производительности и предупреждения#

Производительность отдельных методов с точки зрения скорости значительно варьируется в зависимости от распределения и метода. Результаты метода получаются одним из двух способов: либо путем явного вычисления, либо с помощью универсального алгоритма, не зависящего от конкретного распределения.

Явный расчет, с одной стороны, требует, чтобы метод был напрямую указан для данного распределения, либо через аналитические формулы, либо через специальные функции в scipy.special или numpy.random для rvs. Эти вычисления обычно относительно быстрые.

С другой стороны, общие методы используются, если распределение не задаёт явных вычислений. Для определения распределения достаточно только pdf или cdf; все остальные методы могут быть выведены с использованием численного интегрирования и поиска корней. Однако эти косвенные методы могут быть очень медленно. Например, rgh = stats.gausshyper.rvs(0.5, 2, 2, 2, size=100) создает случайные переменные очень косвенным способом и занимает около 19 секунд для 100 случайных переменных на моем компьютере, в то время как один миллион случайных переменных из стандартного нормального распределения или из t-распределения занимает чуть больше одной секунды.

Оставшиеся проблемы#

Распределения в scipy.stats недавно были исправлены и улучшены и получили значительный набор тестов; однако остаются некоторые проблемы:

  • Распределения были протестированы в некотором диапазоне параметров; однако, в некоторых крайних диапазонах могут оставаться несколько некорректных результатов.

  • Максимальное правдоподобие в fit не работает со стандартными начальными параметрами для всех распределений, и пользователю необходимо предоставить хорошие начальные параметры. Кроме того, для некоторых распределений использование оценщика максимального правдоподобия может быть по своей природе не лучшим выбором.

Построение конкретных распределений#

Следующие примеры показывают, как создавать собственные распределения. Дальнейшие примеры демонстрируют использование распределений и некоторые статистические тесты.

Создание непрерывного распределения, т.е., подкласс rv_continuous#

Создание непрерывных распределений довольно просто.

>>> from scipy import stats
>>> class deterministic_gen(stats.rv_continuous):
...     def _cdf(self, x):
...         return np.where(x < 0, 0., 1.)
...     def _stats(self):
...         return 0., 0., 0., 0.

>>> deterministic = deterministic_gen(name="deterministic")
>>> deterministic.cdf(np.arange(-3, 3, 0.5))
array([ 0.,  0.,  0.,  0.,  0.,  0.,  1.,  1.,  1.,  1.,  1.,  1.])

Интересно, что pdf теперь вычисляется автоматически:

>>> deterministic.pdf(np.arange(-3, 3, 0.5))
array([  0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
         0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
         5.83333333e+04,   4.16333634e-12,   4.16333634e-12,
         4.16333634e-12,   4.16333634e-12,   4.16333634e-12])

Обратите внимание на проблемы производительности, упомянутые в Проблемы производительности и предупреждения. Вычисление неуказанных общих методов может стать очень медленным, поскольку вызываются только общие методы, которые по своей природе не могут использовать какую-либо специфическую информацию о распределении. Таким образом, в качестве предостерегающего примера:

>>> from scipy.integrate import quad
>>> quad(deterministic.pdf, -1e-1, 1e-1)
(4.163336342344337e-13, 0.0)

Но это неверно: интеграл по этой плотности вероятности должен быть равен 1. Сделаем интервал интегрирования меньше:

>>> quad(deterministic.pdf, -1e-3, 1e-3)  # warning removed
(1.000076872229173, 0.0010625571718182458)

Это выглядит лучше. Однако проблема возникла из-за того, что плотность вероятности не указана в определении класса детерминированного распределения.

Создание подклассов rv_discrete#

В следующем мы используем stats.rv_discrete для генерации дискретного распределения, которое имеет вероятности усеченного нормального распределения для интервалов, центрированных вокруг целых чисел.

Общая информация

Из документации rv_discrete, help(stats.rv_discrete),

«Вы можете создать произвольную дискретную случайную величину, где P{X=xk} = pk, передав методу инициализации rv_discrete (через ключевое слово values=) кортеж последовательностей (xk, pk), который описывает только те значения X (xk), которые встречаются с ненулевой вероятностью (pk).»

Помимо этого, для работы этого подхода есть дополнительные требования:

  • Ключевое слово имя требуется.

  • Точки поддержки распределения xk должны быть целыми числами.

  • Необходимо указать количество значащих цифр (десятичных знаков).

Фактически, если последние два требования не выполнены, может быть вызвано исключение или результирующие числа могут быть некорректными.

Пример

Давайте выполним работу. Сначала:

>>> npoints = 20   # number of integer support points of the distribution minus 1
>>> npointsh = npoints // 2
>>> npointsf = float(npoints)
>>> nbound = 4   # bounds for the truncated normal
>>> normbound = (1+1/npointsf) * nbound   # actual bounds of truncated normal
>>> grid = np.arange(-npointsh, npointsh+2, 1)   # integer grid
>>> gridlimitsnorm = (grid-0.5) / npointsh * nbound   # bin limits for the truncnorm
>>> gridlimits = grid - 0.5   # used later in the analysis
>>> grid = grid[:-1]
>>> probs = np.diff(stats.truncnorm.cdf(gridlimitsnorm, -normbound, normbound))
>>> gridint = grid

И, наконец, мы можем создать подкласс rv_discrete:

>>> normdiscrete = stats.rv_discrete(values=(gridint,
...              np.round(probs, decimals=7)), name='normdiscrete')

Теперь, когда мы определили распределение, у нас есть доступ ко всем общим методам дискретных распределений.

>>> print('mean = %6.4f, variance = %6.4f, skew = %6.4f, kurtosis = %6.4f' %
...       normdiscrete.stats(moments='mvsk'))
mean = -0.0000, variance = 6.3302, skew = 0.0000, kurtosis = -0.0076

>>> nd_std = np.sqrt(normdiscrete.stats(moments='v'))

Тестирование реализации

Давайте сгенерируем случайную выборку и сравним наблюдаемые частоты с вероятностями.

>>> n_sample = 500
>>> rvs = normdiscrete.rvs(size=n_sample)
>>> f, l = np.histogram(rvs, bins=gridlimits)
>>> sfreq = np.vstack([gridint, f, probs*n_sample]).T
>>> print(sfreq)
[[-1.00000000e+01  0.00000000e+00  2.95019349e-02]  # random
 [-9.00000000e+00  0.00000000e+00  1.32294142e-01]
 [-8.00000000e+00  0.00000000e+00  5.06497902e-01]
 [-7.00000000e+00  2.00000000e+00  1.65568919e+00]
 [-6.00000000e+00  1.00000000e+00  4.62125309e+00]
 [-5.00000000e+00  9.00000000e+00  1.10137298e+01]
 [-4.00000000e+00  2.60000000e+01  2.24137683e+01]
 [-3.00000000e+00  3.70000000e+01  3.89503370e+01]
 [-2.00000000e+00  5.10000000e+01  5.78004747e+01]
 [-1.00000000e+00  7.10000000e+01  7.32455414e+01]
 [ 0.00000000e+00  7.40000000e+01  7.92618251e+01]
 [ 1.00000000e+00  8.90000000e+01  7.32455414e+01]
 [ 2.00000000e+00  5.50000000e+01  5.78004747e+01]
 [ 3.00000000e+00  5.00000000e+01  3.89503370e+01]
 [ 4.00000000e+00  1.70000000e+01  2.24137683e+01]
 [ 5.00000000e+00  1.10000000e+01  1.10137298e+01]
 [ 6.00000000e+00  4.00000000e+00  4.62125309e+00]
 [ 7.00000000e+00  3.00000000e+00  1.65568919e+00]
 [ 8.00000000e+00  0.00000000e+00  5.06497902e-01]
 [ 9.00000000e+00  0.00000000e+00  1.32294142e-01]
 [ 1.00000000e+01  0.00000000e+00  2.95019349e-02]]
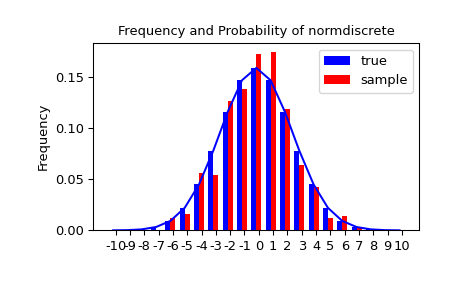
"An X-Y histogram plot showing the distribution of random variates. A blue trace shows a normal bell curve. A blue bar chart perfectly approximates the curve showing the true distribution. A red bar chart representing the sample is well described by the blue trace but not exact."
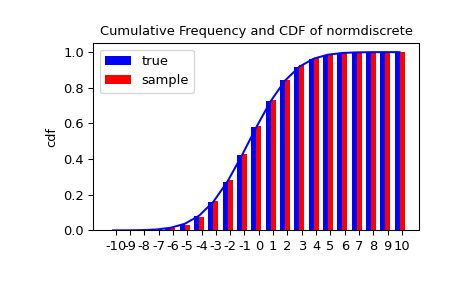
"An X-Y histogram plot showing the cumulative distribution of random variates. A blue trace shows a CDF for a typical normal distribution. A blue bar chart perfectly approximates the curve showing the true distribution. A red bar chart representing the sample is well described by the blue trace but not exact."

Далее мы можем использовать критерий хи-квадрат, scipy.stats.chisquare, чтобы проверить нулевую гипотезу о том, что выборка распределена в соответствии с нашим норм-дискретным распределением.

Тест требует минимального количества наблюдений в каждой корзине. Мы объединяем хвостовые корзины в более крупные, чтобы они содержали достаточно наблюдений.

>>> f2 = np.hstack([f[:5].sum(), f[5:-5], f[-5:].sum()])
>>> p2 = np.hstack([probs[:5].sum(), probs[5:-5], probs[-5:].sum()])
>>> ch2, pval = stats.chisquare(f2, p2*n_sample)

>>> print('chisquare for normdiscrete: chi2 = %6.3f pvalue = %6.4f' % (ch2, pval))
chisquare for normdiscrete: chi2 = 12.466 pvalue = 0.4090  # random

Концептуально, тестовая статистика chi2 чувствителен к отклонениям между частотами наблюдений и их ожидаемыми частотами при нулевой гипотезе. P-значение — это вероятность получения выборок из предполагаемого распределения, которые дали бы более экстремальное значение статистики, чем то, которое мы наблюдали. Наше значение статистики не очень высокое; на самом деле, есть 40,9% вероятность того, что статистика была бы выше 12,466, если бы мы взяли выборку того же размера из дискретного распределения, определенного p2. Следовательно, тест предоставляет мало доказательств против нулевой гипотезы о том, что выборка была взята из нашего норм-дискретного распределения.