numpy.polyfit#

numpy.polyfit(x, y, deg, rcond=None, полный=False, w=None, cov=False)[источник]#

Полиномиальная аппроксимация методом наименьших квадратов.

Примечание

Это часть старого API полиномов. Начиная с версии 1.4, новый API полиномов, определенный в numpy.polynomial предпочтительнее. Сводку различий можно найти в руководство по переходу.

Подобрать полином p[0] * x**deg + ... + p[deg] степени deg к точкам (x, y). Возвращает вектор коэффициентов p который минимизирует квадратичную ошибку в порядке deg, deg-1, … 0.

The Polynomial.fit класс метод рекомендуется для нового кода, так как он более устойчив численно. См. документацию метода для получения дополнительной информации.

Параметры:

xarray_like, shape (M,): x-координаты M точек выборки (x[i], y[i]).
yarray_like, форма (M,) или (M, K): y-координаты точек выборки. Несколько наборов данных точек выборки, использующих одинаковые x-координаты, могут быть обработаны одновременно путём передачи двумерного массива, содержащего один набор данных в каждом столбце.
degint: Степень аппроксимирующего полинома
rcondfloat, опционально: Относительное число обусловленности подгонки. Сингулярные значения, меньшие этого значения относительно наибольшего сингулярного значения, будут проигнорированы. Значение по умолчанию равно len(x)*eps, где eps - относительная точность типа float, обычно около 2e-16.
полныйbool, необязательно: Переключатель, определяющий тип возвращаемого значения. Когда он установлен в False (по умолчанию), возвращаются только коэффициенты; когда в True, также возвращается диагностическая информация из сингулярного разложения.
warray_like, shape (M,), optional: Веса. Если не None, вес w[i] применяется к не возведённому в квадрат остатку y[i] - y_hat[i] в x[i]. В идеале веса выбираются так, чтобы ошибки произведений w[i]*y[i] все имеют одинаковую дисперсию. При использовании взвешивания по обратной дисперсии используйте w[i] = 1/sigma(y[i]). Значение по умолчанию — None.
covbool или str, необязательно: Если задано и не False, возвращать не только оценку, но и её ковариационную матрицу. По умолчанию ковариации масштабируются на chi2/dof, где dof = M - (deg + 1), т.е. веса считаются ненадёжными, кроме как в относительном смысле, и всё масштабируется так, чтобы приведённый chi2 был равен единице. Это масштабирование опускается, если cov='unscaled', что актуально для случая, когда веса w = 1/sigma, где sigma известно как надёжная оценка неопределённости.

Возвращает:

pndarray, форма (deg + 1,) или (deg + 1, K)

Коэффициенты полинома, начиная с высшей степени. Если y был 2-мерным, коэффициенты для k-го набора данных находятся в p[:,k].

остатки, ранг, сингулярные значения, rcond

Эти значения возвращаются только если full == True

остатки – сумма квадратов остатков подгонки методом наименьших квадратов
rank – эффективный ранг масштабированной матрицы коэффициентов Вандермонда
singular_values – сингулярные значения масштабированной матрицы коэффициентов Вандермонда
rcond – значение rcond.

Для более подробной информации см. numpy.linalg.lstsq.

Vndarray, форма (deg + 1, deg + 1) или (deg + 1, deg + 1, K)

Присутствует только если full == False и cov == True. Ковариационная матрица оценок коэффициентов полинома. Диагональ этой матрицы - оценки дисперсии для каждого коэффициента. Если y является двумерным массивом, то ковариационная матрица для k-й набор данных находится в V[:,:,k]

Предупреждает:

RankWarning

Ранг матрицы коэффициентов в методе наименьших квадратов недостаточен. Предупреждение выводится только если full == False.

Предупреждения можно отключить с помощью

>>> import warnings
>>> warnings.simplefilter('ignore', np.exceptions.RankWarning)

Смотрите также

polyval: Вычисление значений полинома.
linalg.lstsq: Вычисляет аппроксимацию методом наименьших квадратов.
scipy.interpolate.UnivariateSpline: Вычисляет сплайн-аппроксимации.

Примечания

Решение минимизирует квадратичную ошибку

\[E = \sum_{j=0}^k |p(x_j) - y_j|^2\]

в уравнениях:

x[0]**n * p[0] + ... + x[0] * p[n-1] + p[n] = y[0]
x[1]**n * p[0] + ... + x[1] * p[n-1] + p[n] = y[1]
...
x[k]**n * p[0] + ... + x[k] * p[n-1] + p[n] = y[k]

Матрица коэффициентов коэффициентов p является матрицей Вандермонда.

polyfit выдает RankWarning когда метод наименьших квадратов плохо обусловлен. Это означает, что наилучшая аппроксимация плохо определена из-за численной ошибки. Результаты могут быть улучшены путём снижения степени полинома или замены x by x - x.mean(). rcond параметр также может быть установлен в значение меньшее, чем по умолчанию, но полученная аппроксимация может быть ложной: включение вкладов от малых сингулярных значений может добавить числовой шум к результату.

Обратите внимание, что подгонка полиномиальных коэффициентов по своей природе плохо обусловлена, когда степень полинома велика или интервал точек выборки плохо центрирован. Качество подгонки всегда следует проверять в этих случаях. Когда полиномиальные подгонки неудовлетворительны, сплайны могут быть хорошей альтернативой.

Ссылки

[1]

Википедия, «Аппроксимация кривых», https://en.wikipedia.org/wiki/Curve_fitting

[2]

Википедия, «Полиномиальная интерполяция», https://en.wikipedia.org/wiki/Polynomial_interpolation

Примеры

>>> import numpy as np
>>> import warnings
>>> x = np.array([0.0, 1.0, 2.0, 3.0,  4.0,  5.0])
>>> y = np.array([0.0, 0.8, 0.9, 0.1, -0.8, -1.0])
>>> z = np.polyfit(x, y, 3)
>>> z
array([ 0.08703704, -0.81349206,  1.69312169, -0.03968254]) # may vary

Удобно использовать poly1d объекты для работы с полиномами:

>>> p = np.poly1d(z)
>>> p(0.5)
0.6143849206349179 # may vary
>>> p(3.5)
-0.34732142857143039 # may vary
>>> p(10)
22.579365079365115 # may vary

Полиномы высокого порядка могут сильно осциллировать:

>>> with warnings.catch_warnings():
...     warnings.simplefilter('ignore', np.exceptions.RankWarning)
...     p30 = np.poly1d(np.polyfit(x, y, 30))
...
>>> p30(4)
-0.80000000000000204 # may vary
>>> p30(5)
-0.99999999999999445 # may vary
>>> p30(4.5)
-0.10547061179440398 # may vary

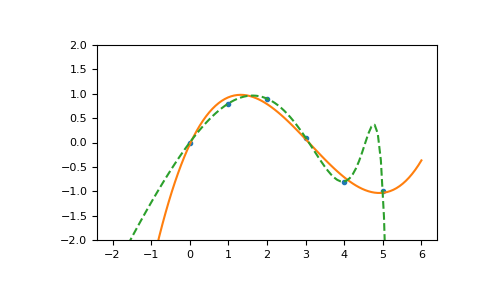
Иллюстрация:

>>> import matplotlib.pyplot as plt
>>> xp = np.linspace(-2, 6, 100)
>>> _ = plt.plot(x, y, '.', xp, p(xp), '-', xp, p30(xp), '--')
>>> plt.ylim(-2,2)
(-2, 2)
>>> plt.show()