numpy.linalg.lstsq

linalg.lstsq(a, b, rcond=None)

Вернуть решение методом наименьших квадратов для линейного матричного уравнения.

Вычисляет вектор x которое приблизительно решает уравнение a @ x = b. Уравнение может быть недоопределённым, хорошо определённым или переопределённым (т.е. количество линейно независимых строк a может быть меньше, равно или больше количества линейно независимых столбцов). Если a является квадратной и полного ранга, тогда x (но из-за ошибок округления) является «точным» решением уравнения. В противном случае, x минимизирует евклидову 2-норму \(||b - ax||\). Если существует несколько минимизирующих решений, выбирается то, у которого наименьшая 2-норма \(||x||\) возвращается.

Параметры:

a(M, N) array_like

Матрица "коэффициентов".

b{(M,), (M, K)} array_like

Значения ординат или "зависимой переменной". Если b является двумерным, решение наименьших квадратов вычисляется для каждого из K столбцы из b.

rcondfloat, опционально

Пороговое отношение для малых сингулярных значений a. Для целей определения ранга сингулярные значения рассматриваются как нулевые, если они меньше, чем rcond умноженное на наибольшее сингулярное значение a. По умолчанию используется машинная точность, умноженная на max(M, N). Передача -1 будет использовать машинную точность.

Изменено в версии 2.0: Ранее значением по умолчанию было -1, но было выдано предупреждение, что это изменится.

Возвращает:

x{(N,), (N, K)} ndarray

Решение методом наименьших квадратов. Если b является двумерным, решения находятся в K столбцы x.

остатки{(1,), (K,), (0,)} ndarray

Суммы квадратов остатков: квадрат евклидовой 2-нормы для каждого столбца в b - a @ x. Если ранг a равно < N или M <= N, это пустой массив. Если b является одномерным, это массив формы (1,). В противном случае форма (K,).

rankint

Ранг матрицы a.

s(min(M, N),) ndarray

Сингулярные значения a.

Вызывает:

LinAlgError

Если вычисление не сходится.

Смотрите также

scipy.linalg.lstsq

Похожая функция в SciPy.

Примечания

Если b является матрицей, тогда все результаты массивов возвращаются как матрицы.

Примеры

Попробуйте в вашем браузере!

Подогнать линию, y = mx + c, через некоторые зашумлённые точки данных:

>>> import numpy as np
>>> x = np.array([0, 1, 2, 3])
>>> y = np.array([-1, 0.2, 0.9, 2.1])

Изучая коэффициенты, мы видим, что линия должна иметь наклон примерно 1 и пересекать ось y примерно в -1.

Мы можем переписать уравнение линии как y = Ap, где A = [[x 1]] и p = [[m], [c]]. Теперь используйте lstsq решить для p:

>>> A = np.vstack([x, np.ones(len(x))]).T
>>> A
array([[ 0.,  1.],
       [ 1.,  1.],
       [ 2.,  1.],
       [ 3.,  1.]])

>>> m, c = np.linalg.lstsq(A, y)[0]
>>> m, c
(1.0 -0.95) # may vary

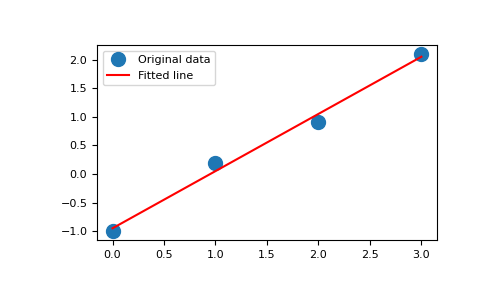
Постройте график данных вместе с подобранной линией:

>>> import matplotlib.pyplot as plt
>>> _ = plt.plot(x, y, 'o', label='Original data', markersize=10)
>>> _ = plt.plot(x, m*x + c, 'r', label='Fitted line')
>>> _ = plt.legend()
>>> plt.show()

НазадОткрыть во вкладке