Кусочно-полиномы и сплайны

Подпрограммы 1D интерполяции рассмотрено в предыдущем разделе, работают, конструируя определенные кусочно полиномы: интерполяционный диапазон разделяется на интервалы так называемыми точки разрыва, и на каждом интервале есть определённый полином. Эти полиномиальные куски затем сопрягаются в точках разрыва с заданной гладкостью: вторые производные для кубических сплайнов, первые производные для монотонных интерполянтов и так далее.

Полином степени \(k\) можно рассматривать как линейную комбинацию \(k+1\) элементы мономиального базиса, \(1, x, x^2, \cdots, x^k\). В некоторых приложениях полезно рассматривать альтернативные (если формально эквивалентные) базисы. Два популярных базиса, реализованных в scipy.interpolate являются B-сплайнами (BSpline) и полиномы Бернштейна (BPoly). B-сплайны часто используются, например, в задачах непараметрической регрессии, а полиномы Бернштейна используются для построения кривых Безье.

PPoly объекты представляют кусочно-полиномиальные функции в 'обычном' степенном базисе. Это верно для CubicSpline экземпляры и монотонные интерполянты. В общем случае, PPoly объекты могут представлять полиномы произвольных порядков, а не только кубические. Для массива данных x, точки разрыва находятся в точках данных, и массив коэффициентов, c , определить полиномы степени \(k\), так что c[i, j] является коэффициентом для (x - x[j])**(k-i) на отрезке между x[j] и x[j+1] .

BSpline объекты представляют B-сплайн функции — линейные комбинации b-сплайновые базисные элементы. Эти объекты могут быть созданы напрямую или сконструированы из данных с помощью make_interp_spline фабричная функция.

Наконец, полиномы Бернштейна представлены как экземпляры BPoly класс.

Все эти классы реализуют (в основном) схожий интерфейс, PPoly является наиболее полным по функциональности. Далее мы рассмотрим основные возможности этого интерфейса и обсудим некоторые детали альтернативных базисов для кусочно-полиномиальных функций.

Манипулирование PPoly объекты

PPoly объекты имеют удобные методы для построения производных и первообразных, вычисления интегралов и нахождения корней. Например, мы табулируем функцию синуса и находим корни её производной.

>>> import numpy as np
>>> from scipy.interpolate import CubicSpline
>>> x = np.linspace(0, 10, 71)
>>> y = np.sin(x)
>>> spl = CubicSpline(x, y)

Теперь продифференцируем сплайн:

>>> dspl = spl.derivative()

Здесь dspl является PPoly экземпляр, который представляет полиномиальную аппроксимацию производной исходного объекта, spl . Вычисление dspl при фиксированном аргументе эквивалентно вычислению исходного сплайна с nu=1 аргумент:

>>> dspl(1.1), spl(1.1, nu=1)
(0.45361436, 0.45361436)

Обратите внимание, что вторая форма выше вычисляет производную на месте, в то время как с dspl объекта, мы можем найти нули производной spl:

>>> dspl.roots() / np.pi
array([-0.45480801,  0.50000034,  1.50000099,  2.5000016 ,  3.46249993])

Это хорошо согласуется с корнями \(\pi/2 + \pi\,n\) of \(\cos(x) = \sin'(x)\). Обратите внимание, что по умолчанию вычисляются корни экстраполированный за пределы интервала интерполяции \(0 \leqslant x \leqslant 10\), и что экстраполированные результаты (первое и последнее значения) гораздо менее точны. Мы можем отключить экстраполяцию и ограничить поиск корней интервалом интерполяции:

>>> dspl.roots(extrapolate=False) / np.pi
array([0.50000034,  1.50000099,  2.5000016])

На самом деле, root метод является частным случаем более общего solve метод, который находит для заданной константы \(y\) решения уравнения \(f(x) = y\) , где \(f(x)\) является кусочно-полиномиальной:

>>> dspl.solve(0.5, extrapolate=False) / np.pi
array([0.33332755, 1.66667195, 2.3333271])

что хорошо согласуется с ожидаемыми значениями \(\pm\arccos(1/2) + 2\pi\,n\).

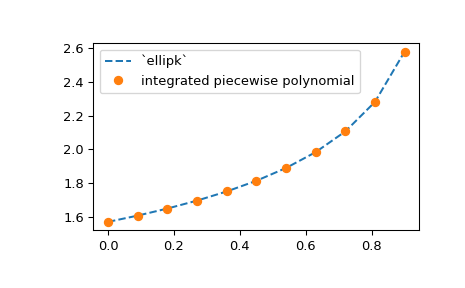
Интегралы кусочно-полиномиальных функций могут быть вычислены с использованием .integrate метод, который принимает нижний и верхний пределы интегрирования. В качестве примера мы вычисляем приближение к полному эллиптическому интегралу \(K(m) = \int_0^{\pi/2} [1 - m\sin^2 x]^{-1/2} dx\):

>>> from scipy.special import ellipk
>>> m = 0.5
>>> ellipk(m)
1.8540746773013719

Для этого мы табулируем подынтегральную функцию и интерполируем её с использованием монотонного интерполянта PCHIP (мы также могли бы использовать CubicSpline):

>>> from scipy.interpolate import PchipInterpolator
>>> x = np.linspace(0, np.pi/2, 70)
>>> y = (1 - m*np.sin(x)**2)**(-1/2)
>>> spl = PchipInterpolator(x, y)

и интегрировать

>>> spl.integrate(0, np.pi/2)
1.854074674965991

что действительно близко к значению, вычисленному scipy.special.ellipk.

Все кусочно-полиномиальные функции могут быть построены с N-мерными y значения. Если y.ndim > 1, это понимается как стек 1D y значения, которые расположены вдоль оси интерполяции (со значением по умолчанию 0). Последнее указывается через axis аргумент, и инвариант заключается в том, что len(x) == y.shape[axis]. В качестве примера мы расширяем пример эллиптического интеграла выше, чтобы вычислить приближение для диапазона m значениям, используя трансляцию NumPy:

>>> from scipy.interpolate import PchipInterpolator
>>> m = np.linspace(0, 0.9, 11)
>>> x = np.linspace(0, np.pi/2, 70)
>>> y = 1 / np.sqrt(1 - m[:, None]*np.sin(x)**2)

Теперь y массив имеет форму (11, 70), так что значения y для фиксированного значения m расположены вдоль второй оси y массив.

>>> spl = PchipInterpolator(x, y, axis=1)  # the default is axis=0
>>> import matplotlib.pyplot as plt
>>> plt.plot(m, spl.integrate(0, np.pi/2), '--')

>>> from scipy.special import ellipk
>>> plt.plot(m, ellipk(m), 'o')
>>> plt.legend(['`ellipk`', 'integrated piecewise polynomial'])
>>> plt.show()

B-сплайны: узлы и коэффициенты

B-сплайн функция — например, построенная из данных через make_interp_spline вызов — определяется так называемым узлы и коэффициенты.

В качестве иллюстрации снова построим интерполяцию функции синуса. Узлы доступны как t атрибут BSpline экземпляр:

>>> x = np.linspace(0, 3/2, 7)
>>> y = np.sin(np.pi*x)
>>> from scipy.interpolate import make_interp_spline
>>> bspl = make_interp_spline(x, y, k=3)
>>> print(bspl.t)
[0.  0.  0.  0.        0.5  0.75  1.        1.5  1.5  1.5  1.5 ]
>>> print(x)
[            0.  0.25  0.5  0.75  1.  1.25  1.5 ]

Мы видим, что вектор узлов по умолчанию строится из входного массива x: сначала он создаётся \((k+1)\) -регулярный (он имеет k повторяющиеся узлы добавляются в начало и конец); затем, вторая и предпоследняя точки входного массива удаляются — это так называемый не-узел граничное условие.

В общем случае, интерполяционный сплайн степени k требуется len(t) - len(x) - k - 1 граничные условия. Для кубических сплайнов с (k+1)-регулярные массивы узлов означают два граничных условия — или удаление двух значений из x массива. Различные граничные условия могут быть запрошены с использованием необязательного bc_type аргумент make_interp_spline.

Коэффициенты b-сплайна доступны через c атрибут BSpline объект:

>>> len(bspl.c)
7

Соглашение заключается в том, что для len(t) узлов там len(t) - k - 1 коэффициенты. Некоторые процедуры (см. Раздел сглаживающих сплайнов) дополнять нулями c массивов так, что len(c) == len(t). Эти дополнительные коэффициенты игнорируются при вычислении.

Мы подчеркиваем, что коэффициенты заданы в b-сплайновый базис, а не степенной базис из \(1, x, \cdots, x^k\).

B-сплайновые базисные элементы

B-сплайн базис используется в различных приложениях, включающих интерполяцию, регрессию и представление кривых. B-сплайны являются кусочно-полиномиальными функциями, представленными как линейные комбинации b-сплайновые базисные элементы — которые сами являются определенными линейными комбинациями обычных мономов, \(x^m\) с \(m=0, 1, \dots, k\).

Свойства B-сплайнов хорошо описаны в литературе (см., например, ссылки, перечисленные в BSpline docstring). Для наших целей достаточно знать, что функция b-сплайна однозначно определяется массивом коэффициентов и массивом так называемых узлы, которые могут совпадать или не совпадать с точками данных, x.

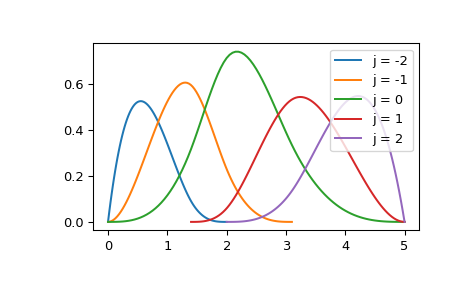
В частности, базисный элемент B-сплайна степени k (например, k=3 для кубических сплайнов) определяется как \(k+2\) узлы и равна нулю вне этих узлов. Для иллюстрации постройте набор ненулевых базисных элементов на определенном интервале:

>>> k = 3      # cubic splines
>>> t = [0., 1.4, 2., 3.1, 5.]   # internal knots
>>> t = np.r_[[0]*k, t, [5]*k]   # add boundary knots

>>> from scipy.interpolate import BSpline
>>> import matplotlib.pyplot as plt
>>> for j in [-2, -1, 0, 1, 2]:
...     a, b = t[k+j], t[-k+j-1]
...     xx = np.linspace(a, b, 101)
...     bspl = BSpline.basis_element(t[k+j:-k+j])
...     plt.plot(xx, bspl(xx), label=f'j = {j}')
>>> plt.legend(loc='best')
>>> plt.show()

Здесь BSpline.basis_element по сути является сокращением для построения сплайна только с одним ненулевым коэффициентом. Например, j=2 элемент в приведенном выше примере эквивалентен

>>> c = np.zeros(t.size - k - 1)
>>> c[-2] = 1
>>> b = BSpline(t, c, k)
>>> np.allclose(b(xx), bspl(xx))
True

При необходимости b-сплайн можно преобразовать в PPoly объект с помощью PPoly.from_spline метод, который принимает BSpline экземпляр и возвращает PPoly экземпляр. Обратное преобразование выполняется BSpline.from_power_basis метод. Однако преобразования между основаниями лучше избегать, так как они накапливают ошибки округления.

Матрицы проектирования в базисе B-сплайнов

Одно из распространенных применений B-сплайнов — непараметрическая регрессия. Причина в том, что локальная природа базисных элементов B-сплайнов делает линейную алгебру ленточной. Это происходит потому, что максимум \(k+1\) базисные элементы ненулевые в данной точке оценки, поэтому матрица плана, построенная на b-сплайнах, имеет не более \(k+1\) диагонали.

В качестве иллюстрации рассмотрим игрушечный пример. Предположим, наши данные одномерны и ограничены интервалом \([0, 6]\). Мы строим 4-регулярный вектор узлов, который соответствует 7 точкам данных и кубическому, k=3, сплайны:

>>> t = [0., 0., 0., 0., 2., 3., 4., 6., 6., 6., 6.]

Далее, примем 'наблюдения' за

>>> xnew = [1, 2, 3]

и построить матрицу плана в разреженном формате CSR

>>> from scipy.interpolate import BSpline
>>> mat = BSpline.design_matrix(xnew, t, k=3)
>>> mat

        with 12 stored elements and shape (3, 7)>

Здесь каждая строка матрицы плана соответствует значению в xnew массив, и строка имеет не более k+1 = 4 ненулевые элементы; строка j содержит базисные элементы, вычисленные в xnew[j]:

>>> with np.printoptions(precision=3):
...     print(mat.toarray())
[[0.125 0.514 0.319 0.042 0.    0.    0.   ]
 [0.    0.111 0.556 0.333 0.    0.    0.   ]
 [0.    0.    0.125 0.75  0.125 0.    0.   ]]

Полиномы Бернштейна, BPoly

Для \(t \in [0, 1]\), полиномы базиса Бернштейна степени \(k\) определяются через

\[b(t; k, a) = C_k^a t^a (1-t)^{k - a}\]

где \(C_k^a\) является биномиальным коэффициентом, и \(a=0, 1, \dots, k\), так что имеется \(k+1\) базисные полиномы степени \(k\).

A BPoly объект представляет собой кусочно Полином Бернштейна в терминах точек разрыва, x, и коэффициенты, c: c[a, j] дает коэффициент для \(b(t; k, a)\) для t на интервале между x[j] и x[j+1].

Пользовательский интерфейс BPoly объектов очень похож на таковой для PPoly объекты: оба могут быть вычислены, продифференцированы и проинтегрированы.

Одна дополнительная особенность BPoly objects является альтернативным конструктором, BPoly.from_derivatives, который создает BPoly объект из значений данных и производных. Конкретно, b = BPoly.from_derivatives(x, y) возвращает вызываемый объект, который интерполирует предоставленные значения, b(x[i]) == y[i]), и имеет предоставленные производные, b(x[i], nu=j) == y[i][j].

Эта операция аналогична CubicHermiteSpline, но он более гибкий, так как может обрабатывать разное количество производных в разных точках данных; т.е., y аргумент может быть списком массивов разной длины. См. BPoly.from_derivatives для дальнейшего обсуждения и примеров.

Преобразование между базисами

В принципе, все три базиса для кусочно-полиномиальных функций (степенной базис, базис Бернштейна и B-сплайны) эквивалентны, и полином в одном базисе может быть преобразован в другой базис. Одна из причин преобразования между базисами заключается в том, что не все базисы реализуют все операции. Например, поиск корней реализован только для PPoly, и, следовательно, для нахождения корней BSpline объект, вам нужно преобразовать в PPoly первый. См. методы PPoly.from_bernstein_basis, PPoly.from_spline, BPoly.from_power_basis, и BSpline.from_power_basis подробности о преобразовании.

В арифметике с плавающей запятой преобразования всегда приводят к некоторой потере точности. Насколько это существенно, зависит от задачи, поэтому рекомендуется проявлять осторожность при преобразовании между основаниями.