numpy.random.RandomState.lognormal

метод

random.RandomState.логнормальное(mean=0.0, sigma=1.0, размер=None)

Извлечь выборки из логнормального распределения.

Генерирует выборки из логнормального распределения с заданным средним, стандартным отклонением и формой массива. Обратите внимание, что среднее и стандартное отклонение относятся не к самому распределению, а к исходному нормальному распределению, из которого оно получено.

Примечание

Новый код должен использовать lognormal метод Generator экземпляр вместо; пожалуйста, смотрите Быстрый старт.

Параметры:

meanfloat или array_like из floats, необязательный

Среднее значение базового нормального распределения. По умолчанию равно 0.

sigmafloat или array_like из floats, необязательный

Стандартное отклонение базового нормального распределения. Должно быть неотрицательным. По умолчанию равно 1.

размерint или кортеж ints, опционально

Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если mean и sigma оба являются скалярами. В противном случае, np.broadcast(mean, sigma).size выбираются образцы.

Возвращает:

выходndarray или скаляр

Выбранные выборки из параметризованного логнормального распределения.

Смотрите также

scipy.stats.lognorm

функция плотности вероятности, распределение, кумулятивная функция распределения и т.д.

random.Generator.lognormal

который следует использовать для нового кода.

Примечания

Переменная x имеет логнормальное распределение, если log(x) распределён нормально. Функция плотности вероятности для логнормального распределения:

\[p(x) = \frac{1}{\sigma x \sqrt{2\pi}} e^{(-\frac{(ln(x)-\mu)^2}{2\sigma^2})}\]

где \(\mu\) является средним значением и \(\sigma\) является стандартным отклонением нормально распределённого логарифма переменной. Логнормальное распределение получается, если случайная величина является product большого числа независимых, одинаково распределённых переменных таким же образом, как нормальное распределение получается, если переменная является sum большого числа независимых, одинаково распределённых переменных.

Ссылки

[1]

Limpert, E., Stahel, W. A., и Abbt, M., "Log-normal Distributions across the Sciences: Keys and Clues," BioScience, Vol. 51, No. 5, May, 2001. https://stat.ethz.ch/~stahel/lognormal/bioscience.pdf

[2]

Reiss, R.D. и Thomas, M., «Statistical Analysis of Extreme Values», Basel: Birkhauser Verlag, 2001, pp. 31-32.

Примеры

Попробуйте в вашем браузере!

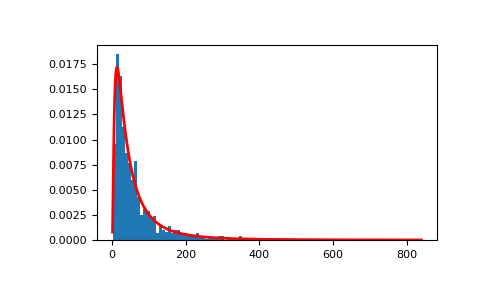
Извлечь выборки из распределения:

>>> mu, sigma = 3., 1. # mean and standard deviation
>>> s = np.random.lognormal(mu, sigma, 1000)

Отображение гистограммы выборок вместе с функцией плотности вероятности:

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 100, density=True, align='mid')

>>> x = np.linspace(min(bins), max(bins), 10000)
>>> pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
...        / (x * sigma * np.sqrt(2 * np.pi)))

>>> plt.plot(x, pdf, linewidth=2, color='r')
>>> plt.axis('tight')
>>> plt.show()

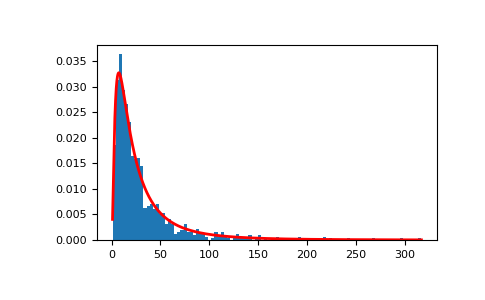
Продемонстрируйте, что произведения случайных выборок из равномерного распределения могут быть хорошо аппроксимированы лог-нормальной функцией плотности вероятности.

>>> # Generate a thousand samples: each is the product of 100 random
>>> # values, drawn from a normal distribution.
>>> b = []
>>> for i in range(1000):
...    a = 10. + np.random.standard_normal(100)
...    b.append(np.prod(a))

>>> b = np.array(b) / np.min(b) # scale values to be positive
>>> count, bins, ignored = plt.hist(b, 100, density=True, align='mid')
>>> sigma = np.std(np.log(b))
>>> mu = np.mean(np.log(b))

>>> x = np.linspace(min(bins), max(bins), 10000)
>>> pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
...        / (x * sigma * np.sqrt(2 * np.pi)))

>>> plt.plot(x, pdf, color='r', linewidth=2)
>>> plt.show()

НазадОткрыть во вкладке