numpy.random.multivariate_normal

random.multivariate_normal(mean, cov, размер=None, check_valid='warn', tol=1e-8)

Сгенерировать случайные выборки из многомерного нормального распределения.

Многомерное нормальное, мультинормальное или гауссово распределение — это обобщение одномерного нормального распределения на более высокие размерности. Такое распределение задается его средним значением и ковариационной матрицей. Эти параметры аналогичны среднему (среднему значению или 'центру') и дисперсии (стандартному отклонению или 'ширине', возведенной в квадрат) одномерного нормального распределения.

Примечание

Новый код должен использовать multivariate_normal метод Generator экземпляр вместо; пожалуйста, смотрите Быстрый старт.

Параметры:

mean1-D array_like, длины N

Среднее N-мерного распределения.

cov2-D array_like, формы (N, N)

Ковариационная матрица распределения. Она должна быть симметричной и положительно полуопределённой для корректной выборки.

размерint или кортеж ints, опционально

При заданной форме, например, (m,n,k), m*n*k образцы генерируются и упаковываются в m-на-n-на-k расположении. Поскольку каждый образец N-мерные, выходная форма (m,n,k,N). Если форма не указана, одиночный (N-D) возвращается образец.

check_valid{ 'warn', 'raise', 'ignore' }, опционально

Поведение, когда ковариационная матрица не является положительно полуопределённой.

tolfloat, опционально

Допуск при проверке сингулярных значений в ковариационной матрице. cov приводится к double перед проверкой.

Возвращает:

выходndarray

Нарисованные выборки, формы размер, если оно было предоставлено. Если нет, форма будет (N,).

Другими словами, каждая запись out[i,j,...,:] является N-мерным значением, взятым из распределения.

Смотрите также

random.Generator.multivariate_normal

который следует использовать для нового кода.

Примечания

Среднее значение — это координата в N-мерном пространстве, которая представляет местоположение, где образцы с наибольшей вероятностью будут сгенерированы. Это аналогично пику колоколообразной кривой для одномерного или однопеременного нормального распределения.

Ковариация указывает степень, с которой две переменные изменяются вместе. Из многомерного нормального распределения мы извлекаем N-мерные выборки, \(X = [x_1, x_2, ... x_N]\). Элемент ковариационной матрицы \(C_{ij}\) является ковариацией \(x_i\) и \(x_j\)Элемент \(C_{ii}\) является дисперсией \(x_i\) (т.е. его «разброс»).

Вместо указания полной ковариационной матрицы популярные приближения включают:

• Сферическая ковариация (cov является кратной единичной матрице)

• Диагональная ковариация (cov имеет неотрицательные элементы, и только на диагонали)

Это геометрическое свойство можно увидеть в двух измерениях, построив сгенерированные точки данных:

>>> mean = [0, 0]
>>> cov = [[1, 0], [0, 100]]  # diagonal covariance

Диагональная ковариация означает, что переменные независимы, а контуры плотности вероятности имеют оси, выровненные по координатным осям:

>>> import matplotlib.pyplot as plt
>>> x, y = np.random.multivariate_normal(mean, cov, 5000).T
>>> plt.plot(x, y, 'x')
>>> plt.axis('equal')
>>> plt.show()

Обратите внимание, что ковариационная матрица должна быть положительно полуопределённой (также называемой неотрицательно-определённой). В противном случае поведение этого метода не определено, и обратная совместимость не гарантируется.

Ссылки

[1]

Папулис, А., «Вероятность, случайные величины и стохастические процессы», 3-е изд., Нью-Йорк: McGraw-Hill, 1991.

[2]

Duda, R. O., Hart, P. E., и Stork, D. G., «Pattern Classification», 2-е изд., Нью-Йорк: Wiley, 2001.

Примеры

Попробуйте в вашем браузере!

>>> mean = (1, 2)
>>> cov = [[1, 0], [0, 1]]
>>> x = np.random.multivariate_normal(mean, cov, (3, 3))
>>> x.shape
(3, 3, 2)

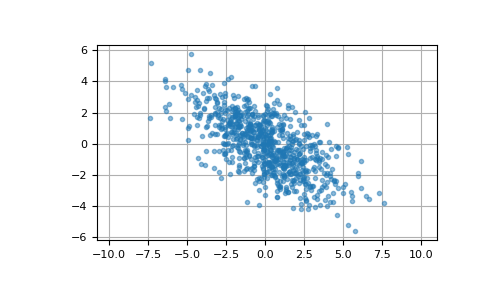
Здесь мы генерируем 800 выборок из двумерного нормального распределения со средним [0, 0] и ковариационной матрицей [[6, -3], [-3, 3.5]]. Ожидаемые дисперсии первой и второй компонент выборки равны 6 и 3.5 соответственно, а ожидаемый коэффициент корреляции составляет -3/sqrt(6*3.5) ≈ -0.65465.

>>> cov = np.array([[6, -3], [-3, 3.5]])
>>> pts = np.random.multivariate_normal([0, 0], cov, size=800)

Проверьте, что среднее значение, ковариация и коэффициент корреляции выборки близки к ожидаемым значениям:

>>> pts.mean(axis=0)
array([ 0.0326911 , -0.01280782])  # may vary
>>> np.cov(pts.T)
array([[ 5.96202397, -2.85602287],
       [-2.85602287,  3.47613949]])  # may vary
>>> np.corrcoef(pts.T)[0, 1]
-0.6273591314603949  # may vary

Мы можем визуализировать эти данные с помощью диаграммы рассеяния. Ориентация облака точек иллюстрирует отрицательную корреляцию компонентов этой выборки.

>>> import matplotlib.pyplot as plt
>>> plt.plot(pts[:, 0], pts[:, 1], '.', alpha=0.5)
>>> plt.axis('equal')
>>> plt.grid()
>>> plt.show()

НазадОткрыть во вкладке