numpy.random.RandomState.pareto

метод

random.RandomState.pareto(a, размер=None)

Извлечение выборок из распределения Парето II или Ломакса с заданной формой.

Распределение Ломакса или Парето II — это сдвинутое распределение Парето. Классическое распределение Парето можно получить из распределения Ломакса, добавив 1 и умножив на параметр масштаба m (см. Примечания). Наименьшее значение распределения Ломакса равно нулю, в то время как для классического распределения Парето оно равно mu, где стандартное распределение Парето имеет положение mu = 1. Lomax также можно рассматривать как упрощённую версию обобщённого распределения Парето (доступного в SciPy), с масштабом, установленным в единицу, и местоположением, установленным в ноль.

Распределение Парето должно быть больше нуля и неограничено сверху. Оно также известно как «правило 80-20». В этом распределении 80 процентов весов находятся в нижних 20 процентах диапазона, а остальные 20 процентов заполняют оставшиеся 80 процентов диапазона.

Примечание

Новый код должен использовать pareto метод Generator экземпляр вместо; пожалуйста, смотрите Быстрый старт.

Параметры:

afloat или array_like из float

Форма распределения. Должна быть положительной.

размерint или кортеж ints, опционально

Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если a является скаляром. В противном случае, np.array(a).size выбираются образцы.

Возвращает:

выходndarray или скаляр

Выборки из параметризованного распределения Парето.

Смотрите также

scipy.stats.lomax

функция плотности вероятности, распределение или интегральная функция распределения и т.д.

scipy.stats.genpareto

функция плотности вероятности, распределение или интегральная функция распределения и т.д.

random.Generator.pareto

который следует использовать для нового кода.

Примечания

Функция плотности вероятности распределения Парето равна

\[p(x) = \frac{am^a}{x^{a+1}}\]

где \(a\) является формой и \(m\) масштаб.

Распределение Парето, названное в честь итальянского экономиста Вильфредо Парето, представляет собой степенное распределение вероятностей, полезное во многих реальных задачах. За пределами экономики его обычно называют распределением Брэдфорда. Парето разработал это распределение для описания распределения богатства в экономике. Оно также нашло применение в страховании, статистике посещений веб-страниц, размерах нефтяных месторождений и многих других задачах, включая частоту загрузки проектов в Sourceforge [1]. Это одно из так называемых "тяжелохвостых" распределений.

Ссылки

[1]

Фрэнсис Хант и Пол Джонсон, О распределении Парето проектов Sourceforge.

[2]

Парето, В. (1896). Курс политической экономии. Лозанна.

[3]

Reiss, R.D., Thomas, M.(2001), Statistical Analysis of Extreme Values, Birkhauser Verlag, Basel, pp 23-30.

[4]

Википедия, "Распределение Парето", https://en.wikipedia.org/wiki/Pareto_distribution

Примеры

Попробуйте в вашем браузере!

Извлечь выборки из распределения:

>>> a, m = 3., 2.  # shape and mode
>>> s = (np.random.pareto(a, 1000) + 1) * m

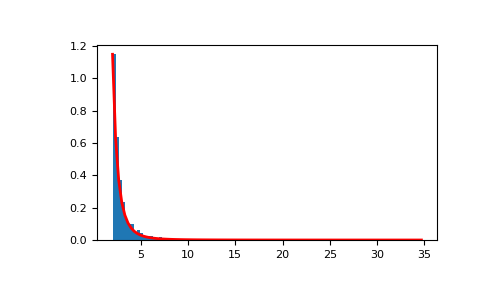
Отобразить гистограмму выборок вместе с функцией плотности вероятности:

>>> import matplotlib.pyplot as plt
>>> count, bins, _ = plt.hist(s, 100, density=True)
>>> fit = a*m**a / bins**(a+1)
>>> plt.plot(bins, max(count)*fit/max(fit), linewidth=2, color='r')
>>> plt.show()

НазадОткрыть во вкладке