numpy.random.power

random.степень(a, размер=None)

Извлекает выборки в [0, 1] из степенного распределения с положительным показателем a - 1.

Также известное как степенное распределение.

Примечание

Новый код должен использовать power метод Generator экземпляр вместо; пожалуйста, смотрите Быстрый старт.

Параметры:

afloat или array_like из float

Параметр распределения. Должен быть неотрицательным.

размерint или кортеж ints, опционально

Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если a является скаляром. В противном случае, np.array(a).size выбираются образцы.

Возвращает:

выходndarray или скаляр

Выбранные образцы из параметризованного степенного распределения.

Вызывает:

ValueError

Если a <= 0.

Смотрите также

random.Generator.power

который следует использовать для нового кода.

Примечания

Функция плотности вероятности равна

\[P(x; a) = ax^{a-1}, 0 \le x \le 1, a>0.\]

Распределение степенной функции — это просто обратное распределение Парето. Его также можно рассматривать как частный случай бета-распределения.

Используется, например, при моделировании завышения страховых претензий.

Ссылки

[1]

Кристиан Кляйбер, Самуэль Котц, «Статистические распределения размеров в экономике и актуарных науках», Wiley, 2003.

[2]

Хекерт, Н. А. и Филибен, Джеймс Дж. «Справочник NIST 148: Справочное руководство Dataplot, Том 2: Подкоманды Let и библиотечные функции», Серия справочников Национального института стандартов и технологий, июнь 2003 г. https://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/powpdf.pdf

Примеры

Попробуйте в вашем браузере!

Извлечь выборки из распределения:

>>> a = 5. # shape
>>> samples = 1000
>>> s = np.random.power(a, samples)

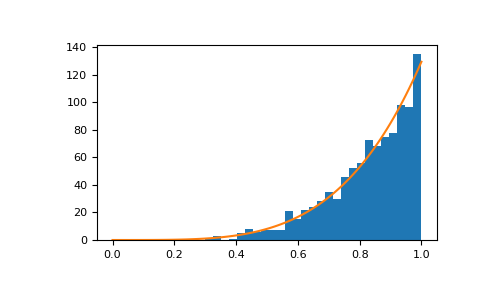
Отображение гистограммы выборок вместе с функцией плотности вероятности:

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, bins=30)
>>> x = np.linspace(0, 1, 100)
>>> y = a*x**(a-1.)
>>> normed_y = samples*np.diff(bins)[0]*y
>>> plt.plot(x, normed_y)
>>> plt.show()

Сравните распределение степенной функции с обратным распределением Парето.

>>> from scipy import stats 
>>> rvs = np.random.power(5, 1000000)
>>> rvsp = np.random.pareto(5, 1000000)
>>> xx = np.linspace(0,1,100)
>>> powpdf = stats.powerlaw.pdf(xx,5)  

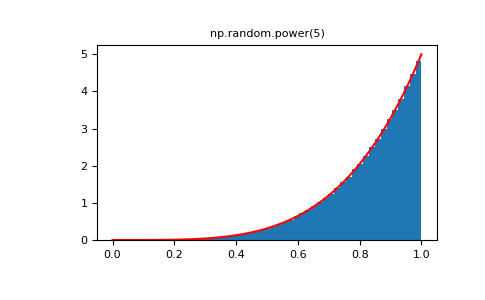
>>> plt.figure()
>>> plt.hist(rvs, bins=50, density=True)
>>> plt.plot(xx,powpdf,'r-')  
>>> plt.title('np.random.power(5)')

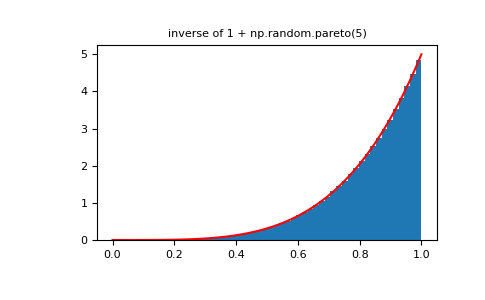
>>> plt.figure()
>>> plt.hist(1./(1.+rvsp), bins=50, density=True)
>>> plt.plot(xx,powpdf,'r-')  
>>> plt.title('inverse of 1 + np.random.pareto(5)')

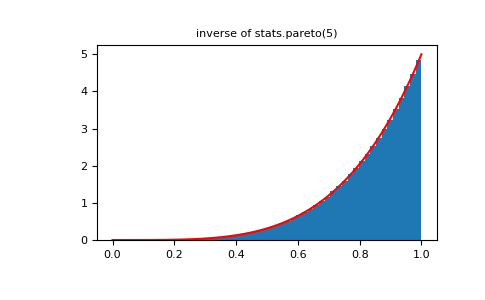
>>> plt.figure()
>>> plt.hist(1./(1.+rvsp), bins=50, density=True)
>>> plt.plot(xx,powpdf,'r-')  
>>> plt.title('inverse of stats.pareto(5)')

НазадОткрыть во вкладке