numpy.random.noncentral_chisquare

random.noncentral_chisquare(df, nonc, размер=None)

Извлеките выборки из нецентрального распределения хи-квадрат.

Некцентральный \(\chi^2\) распределение является обобщением \(\chi^2\) распределение.

Примечание

Новый код должен использовать noncentral_chisquare метод Generator экземпляр вместо; пожалуйста, смотрите Быстрый старт.

Параметры:

dffloat или array_like из float

Степени свободы, должны быть > 0.

noncfloat или array_like из float

Нецентральность, должна быть неотрицательной.

размерint или кортеж ints, опционально

Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если df и nonc оба являются скалярами. В противном случае, np.broadcast(df, nonc).size выбираются образцы.

Возвращает:

выходndarray или скаляр

Выбранные выборки из параметризованного распределения нецентрального хи-квадрат.

Смотрите также

random.Generator.noncentral_chisquare

который следует использовать для нового кода.

Примечания

Функция плотности вероятности для нецентрального распределения хи-квадрат равна

\[P(x;df,nonc) = \sum^{\infty}_{i=0} \frac{e^{-nonc/2}(nonc/2)^{i}}{i!} P_{Y_{df+2i}}(x),\]

где \(Y_{q}\) это Хи-квадрат с q степенями свободы.

Ссылки

[1]

Википедия, «Нецентральное хи-квадрат распределение» https://en.wikipedia.org/wiki/Noncentral_chi-squared_distribution

Примеры

Попробуйте в вашем браузере!

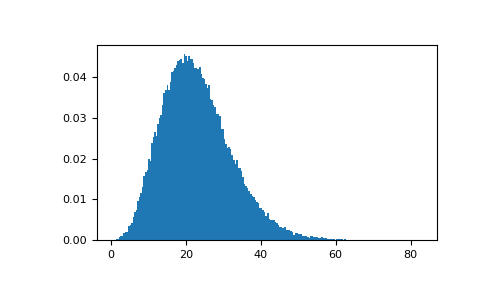
Извлеките значения из распределения и постройте гистограмму

>>> import matplotlib.pyplot as plt
>>> values = plt.hist(np.random.noncentral_chisquare(3, 20, 100000),
...                   bins=200, density=True)
>>> plt.show()

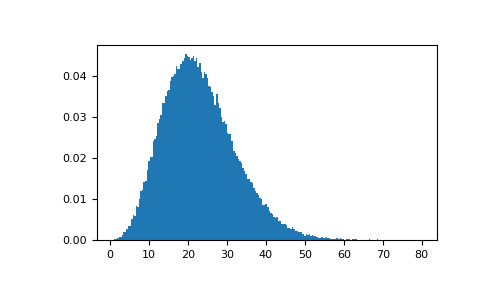
Извлечь значения из нецентрального хи-квадрата с очень маленькой нецентральностью и сравнить с хи-квадратом.

>>> plt.figure()
>>> values = plt.hist(np.random.noncentral_chisquare(3, .0000001, 100000),
...                   bins=np.arange(0., 25, .1), density=True)
>>> values2 = plt.hist(np.random.chisquare(3, 100000),
...                    bins=np.arange(0., 25, .1), density=True)
>>> plt.plot(values[1][0:-1], values[0]-values2[0], 'ob')
>>> plt.show()

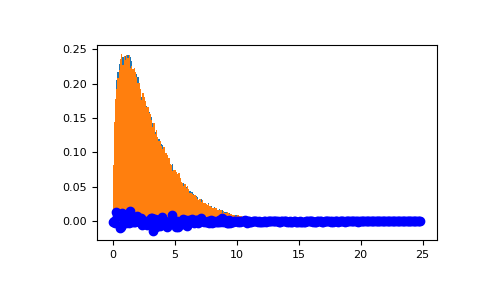
Продемонстрируйте, как большие значения нецентральности приводят к более симметричному распределению.

>>> plt.figure()
>>> values = plt.hist(np.random.noncentral_chisquare(3, 20, 100000),
...                   bins=200, density=True)
>>> plt.show()

НазадОткрыть во вкладке