numpy.random.weibull#

random.weibull(a, размер=None)#

Извлечь выборки из распределения Вейбулла.

Генерирует выборки из распределения Вейбулла с одним параметром и заданным параметром формы a.

\[X = (-ln(U))^{1/a}\]

Здесь U выбирается из равномерного распределения на интервале (0,1].

Более распространённое 2-параметрическое распределение Вейбулла, включая параметр масштаба \(\lambda\) это просто \(X = \lambda(-ln(U))^{1/a}\).

Примечание

Новый код должен использовать weibull метод Generator экземпляр вместо; пожалуйста, смотрите Быстрый старт.

Параметры:

afloat или array_like из float: Параметр формы распределения. Должен быть неотрицательным.
размерint или кортеж ints, опционально: Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если a является скаляром. В противном случае, np.array(a).size выбираются образцы.

Возвращает:

выходndarray или скаляр: Выбранные выборки из параметризованного распределения Вейбулла.

Смотрите также

scipy.stats.weibull_max
scipy.stats.weibull_min
scipy.stats.genextreme
gumbel
random.Generator.weibull: который следует использовать для нового кода.

Примечания

Распределение Вейбулла (или асимптотическое распределение экстремальных значений типа III для наименьших значений, SEV типа III, или распределение Розина-Раммлера) является одним из класса обобщённых распределений экстремальных значений (GEV), используемых при моделировании задач экстремальных значений. Этот класс включает распределения Гумбеля и Фреше.

Функция плотности вероятности распределения Вейбулла равна

\[p(x) = \frac{a} {\lambda}(\frac{x}{\lambda})^{a-1}e^{-(x/\lambda)^a},\]

где \(a\) является формой и \(\lambda\) масштаб.

Функция имеет пик (моду) в \(\lambda(\frac{a-1}{a})^{1/a}\).

Когда a = 1, распределение Вейбулла сводится к экспоненциальному распределению.

Ссылки

[1]

Валодди Вейбулл, Королевский технический университет, Стокгольм, 1939 «Статистическая теория прочности материалов», Ingeniorsvetenskapsakademiens Handlingar Nr 151, 1939, Generalstabens Litografiska Anstalts Forlag, Стокгольм.

[2]

Вальодди Вейбулл, "Статистическая функция распределения широкой применимости", Journal Of Applied Mechanics ASME Paper 1951.

[3]

Википедия, "Распределение Вейбулла", https://en.wikipedia.org/wiki/Weibull_distribution

Примеры

Извлечь выборки из распределения:

>>> a = 5. # shape
>>> s = np.random.weibull(a, 1000)

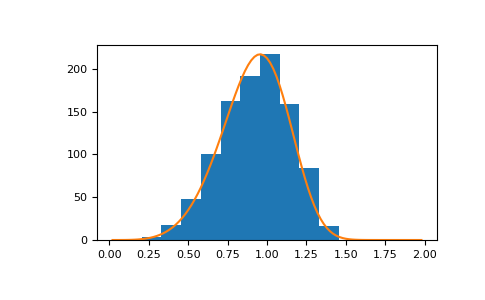
Отображение гистограммы выборок вместе с функцией плотности вероятности:

>>> import matplotlib.pyplot as plt
>>> x = np.arange(1,100.)/50.
>>> def weib(x,n,a):
...     return (a / n) * (x / n)**(a - 1) * np.exp(-(x / n)**a)

>>> count, bins, ignored = plt.hist(np.random.weibull(5.,1000))
>>> x = np.arange(1,100.)/50.
>>> scale = count.max()/weib(x, 1., 5.).max()
>>> plt.plot(x, weib(x, 1., 5.)*scale)
>>> plt.show()

../../../_images/numpy-random-weibull-1.png