numpy.random.zipf#

random.zipf(a, размер=None)#

Генерация выборок из распределения Ципфа.

Выборки берутся из распределения Ципфа с заданным параметром a > 1.

Распределение Ципфа (также известное как дзета-распределение) - это дискретное распределение вероятностей, которое удовлетворяет закону Ципфа: частота элемента обратно пропорциональна его рангу в таблице частот.

Примечание

Новый код должен использовать zipf метод Generator экземпляр вместо; пожалуйста, смотрите Быстрый старт.

Параметры:

afloat или array_like из float: Параметр распределения. Должен быть больше 1.
размерint или кортеж ints, опционально: Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если a является скаляром. В противном случае, np.array(a).size выбираются образцы.

Возвращает:

выходndarray или скаляр: Выборки, взятые из параметризованного распределения Ципфа.

Смотрите также

scipy.stats.zipf: функция плотности вероятности, распределение или функция кумулятивной плотности и т.д.
random.Generator.zipf: который следует использовать для нового кода.

Примечания

Функция вероятности (PMF) для распределения Ципфа

\[p(k) = \frac{k^{-a}}{\zeta(a)},\]

для целых чисел \(k \geq 1\), где \(\zeta\) является дзета-функцией Римана.

Назван в честь американского лингвиста Джорджа Кингсли Ципфа, который отметил, что частота любого слова в выборке языка обратно пропорциональна его рангу в таблице частот.

Ссылки

[1]

Zipf, G. K., "Selected Studies of the Principle of Relative Frequency in Language," Cambridge, MA: Harvard Univ. Press, 1932.

Примеры

Извлечь выборки из распределения:

>>> a = 4.0
>>> n = 20000
>>> s = np.random.zipf(a, n)

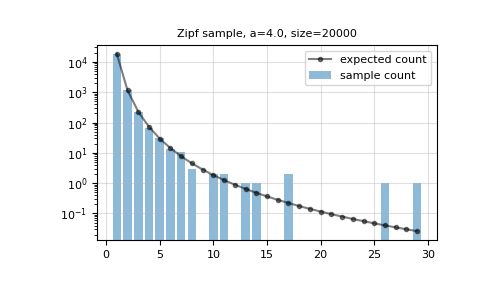
Отобразить гистограмму выборок вместе с ожидаемой гистограммой на основе функции плотности вероятности:

>>> import matplotlib.pyplot as plt
>>> from scipy.special import zeta  

bincount предоставляет быструю гистограмму для маленьких целых чисел.

>>> count = np.bincount(s)
>>> k = np.arange(1, s.max() + 1)

>>> plt.bar(k, count[1:], alpha=0.5, label='sample count')
>>> plt.plot(k, n*(k**-a)/zeta(a), 'k.-', alpha=0.5,
...          label='expected count')   
>>> plt.semilogy()
>>> plt.grid(alpha=0.4)
>>> plt.legend()
>>> plt.title(f'Zipf sample, a={a}, size={n}')
>>> plt.show()

../../../_images/numpy-random-zipf-1.png