numpy.random.standard_t

random.standard_t(df, размер=None)

Извлечение выборок из стандартного распределения Стьюдента с df степени свободы.

Частный случай гиперболического распределения. Как df становится большим, результат напоминает результат стандартного нормального распределения (standard_normal).

Примечание

Новый код должен использовать standard_t метод Generator экземпляр вместо; пожалуйста, смотрите Быстрый старт.

Параметры:

dffloat или array_like из float

Степени свободы, должны быть > 0.

размерint или кортеж ints, опционально

Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если df является скаляром. В противном случае, np.array(df).size выбираются образцы.

Возвращает:

выходndarray или скаляр

Выборки из параметризованного стандартного распределения Стьюдента.

Смотрите также

random.Generator.standard_t

который следует использовать для нового кода.

Примечания

Функция плотности вероятности для t-распределения

\[P(x, df) = \frac{\Gamma(\frac{df+1}{2})}{\sqrt{\pi df} \Gamma(\frac{df}{2})}\Bigl( 1+\frac{x^2}{df} \Bigr)^{-(df+1)/2}\]

t-тест основан на предположении, что данные поступают из нормального распределения. t-тест предоставляет способ проверить, является ли выборочное среднее (то есть среднее, рассчитанное из данных) хорошей оценкой истинного среднего.

Вывод t-распределения был впервые опубликован в 1908 году Уильямом Госсетом во время работы на пивоварню Guinness в Дублине. Из-за проблем с собственностью ему пришлось публиковаться под псевдонимом, поэтому он использовал имя Student.

Ссылки

[1]

Далгаард, Питер, «Вводная статистика с R», Springer, 2002.

[2]

Википедия, 'Распределение Стьюдента' https://en.wikipedia.org/wiki/Student’s_t-distribution

Примеры

Попробуйте в вашем браузере!

Из Dalgaard, страница 83 [1], предположим, что ежедневное потребление энергии для 11 женщин в килоджоулях (кДж) составляет:

>>> intake = np.array([5260., 5470, 5640, 6180, 6390, 6515, 6805, 7515, \
...                    7515, 8230, 8770])

Отличается ли их потребление энергии систематически от рекомендуемого значения 7725 кДж? Наша нулевая гипотеза будет отсутствием отклонения, а альтернативная гипотеза будет наличием эффекта, который может быть либо положительным, либо отрицательным, что делает наш тест двусторонним.

Поскольку мы оцениваем среднее значение и имеем N=11 значений в нашей выборке, у нас есть N-1=10 степеней свободы. Мы устанавливаем уровень значимости 95% и вычисляем t-статистику, используя эмпирическое среднее и эмпирическое стандартное отклонение нашего потребления. Мы используем ddof=1 для вычисления эмпирического стандартного отклонения на основе несмещённой оценки дисперсии (примечание: окончательная оценка не является несмещённой из-за вогнутой природы квадратного корня).

>>> np.mean(intake)
6753.636363636364
>>> intake.std(ddof=1)
1142.1232221373727
>>> t = (np.mean(intake)-7725)/(intake.std(ddof=1)/np.sqrt(len(intake)))
>>> t
-2.8207540608310198

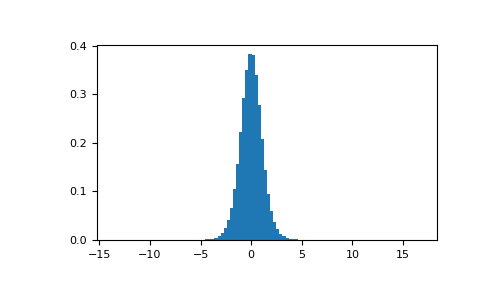
Мы извлекаем 1000000 выборок из распределения Стьюдента с соответствующими степенями свободы.

>>> import matplotlib.pyplot as plt
>>> s = np.random.standard_t(10, size=1000000)
>>> h = plt.hist(s, bins=100, density=True)

Попадает ли наша t-статистика в одну из двух критических областей, найденных на обоих хвостах распределения?

>>> np.sum(np.abs(t) < np.abs(s)) / float(len(s))
0.018318  #random < 0.05, statistic is in critical region

Значение вероятности для этого двустороннего теста составляет около 1,83%, что ниже предопределенного порога значимости в 5%.

Следовательно, вероятность наблюдения значений, столь же экстремальных, как наше условие ввода, при условии истинности нулевой гипотезы слишком низка, и мы отвергаем нулевую гипотезу об отсутствии отклонения.

НазадОткрыть во вкладке