numpy.random.gamma#

random.gamma(shape, scale=1.0, размер=None)#

Извлечение выборок из гамма-распределения.

Выборки берутся из гамма-распределения с заданными параметрами, shape (иногда обозначается как «k») и scale (иногда обозначается как "theta"), где оба параметра > 0.

Примечание

Новый код должен использовать gamma метод Generator экземпляр вместо; пожалуйста, смотрите Быстрый старт.

Параметры:

shapefloat или array_like из float: Форма гамма-распределения. Должна быть неотрицательной.
scalefloat или array_like из floats, необязательный: Масштаб гамма-распределения. Должен быть неотрицательным. По умолчанию равен 1.
размерint или кортеж ints, опционально: Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если shape и scale оба являются скалярами. В противном случае, np.broadcast(shape, scale).size выбираются образцы.

Возвращает:

выходndarray или скаляр: Выбранные образцы из параметризованного гамма-распределения.

Смотрите также

scipy.stats.gamma: функция плотности вероятности, распределение или интегральная функция распределения и т.д.
random.Generator.gamma: который следует использовать для нового кода.

Примечания

Функция плотности вероятности для гамма-распределения равна

\[p(x) = x^{k-1}\frac{e^{-x/\theta}}{\theta^k\Gamma(k)},\]

где \(k\) является формой и \(\theta\) масштаб, и \(\Gamma\) является гамма-функцией.

Гамма-распределение часто используется для моделирования времени до отказа электронных компонентов и возникает естественным образом в процессах, для которых время ожидания между событиями, распределёнными по Пуассону, является значимым.

Ссылки

[1]

Вайсштейн, Эрик В. «Гамма-распределение». Из MathWorld – веб-ресурс Wolfram. https://mathworld.wolfram.com/GammaDistribution.html

[2]

Википедия, "Гамма-распределение", https://en.wikipedia.org/wiki/Gamma_distribution

Примеры

Извлечь выборки из распределения:

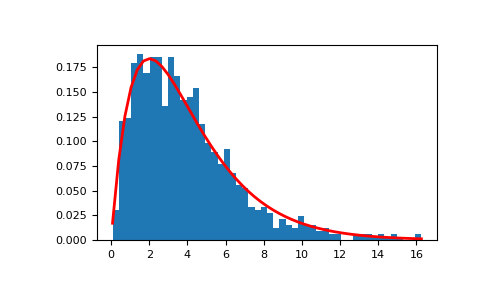
>>> shape, scale = 2., 2.  # mean=4, std=2*sqrt(2)
>>> s = np.random.gamma(shape, scale, 1000)

Отображение гистограммы выборок вместе с функцией плотности вероятности:

>>> import matplotlib.pyplot as plt
>>> import scipy.special as sps  
>>> count, bins, ignored = plt.hist(s, 50, density=True)
>>> y = bins**(shape-1)*(np.exp(-bins/scale) /  
...                      (sps.gamma(shape)*scale**shape))
>>> plt.plot(bins, y, linewidth=2, color='r')  
>>> plt.show()

../../../_images/numpy-random-gamma-1.png