numpy.random.Generator.binomial

метод

random.Generator.биномиальный(n, p, размер=None)

Генерация выборок из биномиального распределения.

Выборки берутся из биномиального распределения с заданными параметрами: n испытаний и p вероятностью успеха, где n — целое число >= 0, а p находится в интервале [0,1]. (n может быть введено как число с плавающей точкой, но при использовании оно усекается до целого числа)

Параметры:

nint или array_like из int

Параметр распределения, >= 0. Дробные числа также принимаются, но будут усечены до целых.

pfloat или array_like из float

Параметр распределения, >= 0 и <=1.

размерint или кортеж ints, опционально

Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если n и p оба являются скалярами. В противном случае, np.broadcast(n, p).size выбираются образцы.

Возвращает:

выходndarray или скаляр

Выбранные образцы из параметризованного биномиального распределения, где каждый образец равен количеству успехов за n испытаний.

Смотрите также

scipy.stats.binom

функция плотности вероятности, распределение или интегральная функция распределения и т.д.

Примечания

Функция вероятности (PMF) для биномиального распределения

\[P(N) = \binom{n}{N}p^N(1-p)^{n-N},\]

где \(n\) — количество испытаний, \(p\) это вероятность успеха, и \(N\) — это количество успехов.

При оценке стандартной ошибки доли в популяции с использованием случайной выборки нормальное распределение работает хорошо, если только произведение p*n <=5, где p = оценка доли популяции, а n = количество выборок, в этом случае вместо него используется биномиальное распределение. Например, выборка из 15 человек показывает 4 левшей и 11 правшей. Тогда p = 4/15 = 27%. 0.27*15 = 4, поэтому в этом случае следует использовать биномиальное распределение.

Ссылки

[1]

Далгаард, Питер, «Введение в статистику с R», Springer-Verlag, 2002.

[2]

Гланц, Стэнтон А. «Primer of Biostatistics.», McGraw-Hill, Пятое издание, 2002.

[3]

Лентнер, Марвин, "Элементарная прикладная статистика", Богден и Куигли, 1972.

[4]

Вайсштейн, Эрик В. «Биномиальное распределение». Из MathWorld – ресурс Wolfram. https://mathworld.wolfram.com/BinomialDistribution.html

[5]

Википедия, «Биномиальное распределение», https://en.wikipedia.org/wiki/Binomial_distribution

Примеры

Попробуйте в вашем браузере!

Извлечь выборки из распределения:

>>> rng = np.random.default_rng()
>>> n, p, size = 10, .5, 10000
>>> s = rng.binomial(n, p, 10000)

Предположим, компания бурит 9 разведочных нефтяных скважин, каждая с оценочной вероятностью успеха p=0.1. Все девять скважин выходят из строя. Какова вероятность этого события?

Более size = 20,000 испытаний вероятность этого события в среднем составляет:

>>> n, p, size = 9, 0.1, 20000
>>> np.sum(rng.binomial(n=n, p=p, size=size) == 0)/size
0.39015  # may vary

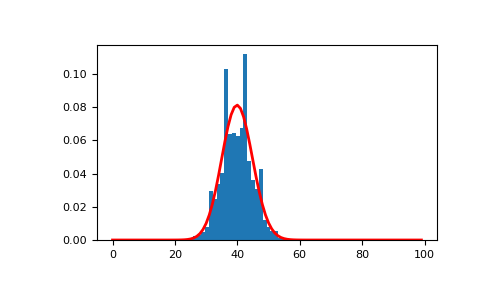
Следующее можно использовать для визуализации образца с n=100, p=0.4 и соответствующая функция плотности вероятности:

>>> import matplotlib.pyplot as plt
>>> from scipy.stats import binom
>>> n, p, size = 100, 0.4, 10000
>>> sample = rng.binomial(n, p, size=size)
>>> count, bins, _ = plt.hist(sample, 30, density=True)
>>> x = np.arange(n)
>>> y = binom.pmf(x, n, p)
>>> plt.plot(x, y, linewidth=2, color='r')

НазадОткрыть во вкладке