numpy.random.Generator.logistic#

метод

random.Generator.логистическая(loc=0.0, scale=1.0, размер=None)#

Извлечь выборки из логистического распределения.

Выборки берутся из логистического распределения с заданными параметрами: loc (положение или среднее, также медиана) и scale (>0).

Параметры:

locfloat или array_like из floats, необязательный: Параметр распределения. По умолчанию равен 0.
scalefloat или array_like из floats, необязательный: Параметр распределения. Должен быть неотрицательным. По умолчанию равен 1.
размерint или кортеж ints, опционально: Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если loc и scale оба являются скалярами. В противном случае, np.broadcast(loc, scale).size выбираются образцы.

Возвращает:

выходndarray или скаляр: Выбранные выборки из параметризованного логистического распределения.

Смотрите также

scipy.stats.logistic: функция плотности вероятности, распределение или интегральная функция распределения и т.д.

Примечания

Функция плотности вероятности для логистического распределения:

\[P(x) = \frac{e^{-(x-\mu)/s}}{s(1+e^{-(x-\mu)/s})^2},\]

где \(\mu\) = местоположение и \(s\) = масштаб.

Логистическое распределение используется в задачах экстремальных значений, где оно может выступать как смесь распределений Гумбеля, в эпидемиологии и Всемирной шахматной федерацией (FIDE), где оно используется в системе рейтинга Эло, предполагая, что производительность каждого игрока — это случайная величина с логистическим распределением.

Ссылки

[1]

Reiss, R.-D. and Thomas M. (2001), «Statistical Analysis of Extreme Values, from Insurance, Finance, Hydrology and Other Fields,» Birkhauser Verlag, Basel, стр. 132-133.

[2]

Вайсштейн, Эрик В. «Логистическое распределение». Из MathWorld — веб-ресурса Wolfram. https://mathworld.wolfram.com/LogisticDistribution.html

[3]

Википедия, «Логистическое распределение», https://en.wikipedia.org/wiki/Logistic_distribution

Примеры

Извлечь выборки из распределения:

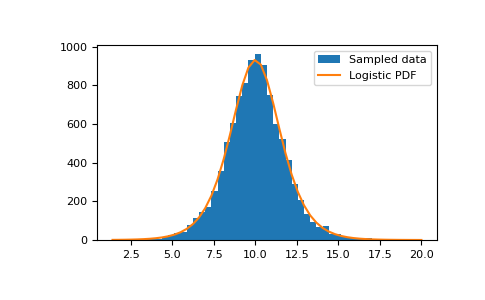
>>> loc, scale = 10, 1
>>> rng = np.random.default_rng()
>>> s = rng.logistic(loc, scale, 10000)
>>> import matplotlib.pyplot as plt
>>> count, bins, _ = plt.hist(s, bins=50, label='Sampled data')

# построить выборочные данные против точного распределения

>>> def logistic(x, loc, scale):
...     return np.exp((loc-x)/scale)/(scale*(1+np.exp((loc-x)/scale))**2)
>>> logistic_values  = logistic(bins, loc, scale)
>>> bin_spacing = np.mean(np.diff(bins))
>>> plt.plot(bins, logistic_values  * bin_spacing * s.size, label='Logistic PDF')
>>> plt.legend()
>>> plt.show()

../../../_images/numpy-random-Generator-logistic-1.png