numpy.random.Generator.geometric#

метод

random.Generator.геометрический(p, размер=None)#

Извлечение выборок из геометрического распределения.

Испытания Бернулли — это эксперименты с одним из двух исходов: успех или неудача (пример такого эксперимента — подбрасывание монеты). Геометрическое распределение моделирует количество испытаний, которые должны быть проведены для достижения успеха. Оно определено на положительных целых числах, k = 1, 2, ....

Функция вероятности геометрического распределения

\[f(k) = (1 - p)^{k - 1} p\]

где p это вероятность успеха отдельного испытания.

Параметры:

pfloat или array_like из float: Вероятность успеха отдельного испытания.
размерint или кортеж ints, опционально: Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если p является скаляром. В противном случае, np.array(p).size выбираются образцы.

Возвращает:

выходndarray или скаляр: Выбранные выборки из параметризованного геометрического распределения.

Ссылки

[1]

Википедия, "Геометрическое распределение", https://en.wikipedia.org/wiki/Geometric_distribution

Примеры

Извлечь 10 000 значений из геометрического распределения, с вероятностью индивидуального успеха, равной p = 0.35:

>>> p, size = 0.35, 10000
>>> rng = np.random.default_rng()
>>> sample = rng.geometric(p=p, size=size)

Какая доля испытаний завершилась успешно после одного запуска?

>>> (sample == 1).sum()/size
0.34889999999999999  # may vary

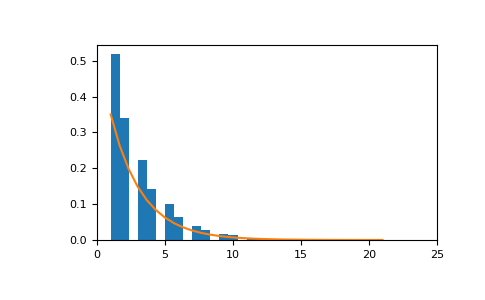
Геометрическое распределение с p=0.35 выглядит следующим образом:

>>> import matplotlib.pyplot as plt
>>> count, bins, _ = plt.hist(sample, bins=30, density=True)
>>> plt.plot(bins, (1-p)**(bins-1)*p)
>>> plt.xlim([0, 25])
>>> plt.show()

../../../_images/numpy-random-Generator-geometric-1.png