numpy.random.Generator.laplace

метод

random.Generator.laplace(loc=0.0, scale=1.0, размер=None)

Извлечение выборок из распределения Лапласа или двойного экспоненциального распределения с указанным местоположением (или средним) и масштабом (затуханием).

Распределение Лапласа похоже на гауссово/нормальное распределение, но имеет более острый пик и более тяжёлые хвосты. Оно представляет разность двух независимых, одинаково распределённых экспоненциальных случайных величин.

Параметры:

locfloat или array_like из floats, необязательный

Позиция, \(\mu\), пика распределения. По умолчанию 0.

scalefloat или array_like из floats, необязательный

\(\lambda\), экспоненциальное затухание. По умолчанию 1. Должно быть неотрицательным.

размерint или кортеж ints, опционально

Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если loc и scale оба являются скалярами. В противном случае, np.broadcast(loc, scale).size выбираются образцы.

Возвращает:

выходndarray или скаляр

Выборки, взятые из параметризованного распределения Лапласа.

Примечания

Он имеет функцию плотности вероятности

\[f(x; \mu, \lambda) = \frac{1}{2\lambda} \exp\left(-\frac{|x - \mu|}{\lambda}\right).\]

Первый закон Лапласа, с 1774 года, утверждает, что частота ошибки может быть выражена как экспоненциальная функция абсолютной величины ошибки, что приводит к распределению Лапласа. Для многих задач в экономике и науках о здоровье это распределение, по-видимому, лучше моделирует данные, чем стандартное распределение Гаусса.

Ссылки

[1]

Абрамовиц, М. и Стегун, И. А. (ред.). «Справочник по математическим функциям с формулами, графиками и математическими таблицами, 9-е издание», Нью-Йорк: Dover, 1972.

[2]

Котц, Самуэль и др. “Распределение Лапласа и обобщения”, Биркхойзер, 2001.

[3]

Weisstein, Eric W. “Laplace Distribution.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/LaplaceDistribution.html

[4]

Википедия, «Распределение Лапласа», https://en.wikipedia.org/wiki/Laplace_distribution

Примеры

Попробуйте в вашем браузере!

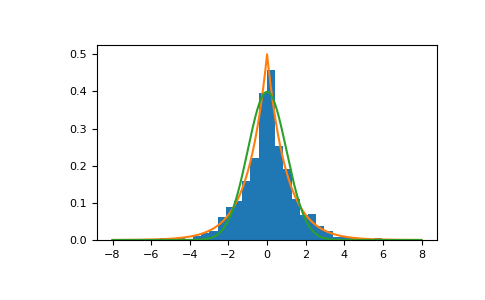
Извлечение выборок из распределения

>>> loc, scale = 0., 1.
>>> rng = np.random.default_rng()
>>> s = rng.laplace(loc, scale, 1000)

Отображение гистограммы выборок вместе с функцией плотности вероятности:

>>> import matplotlib.pyplot as plt
>>> count, bins, _ = plt.hist(s, 30, density=True)
>>> x = np.arange(-8., 8., .01)
>>> pdf = np.exp(-abs(x-loc)/scale)/(2.*scale)
>>> plt.plot(x, pdf)

Постройте гауссову кривую для сравнения:

>>> g = (1/(scale * np.sqrt(2 * np.pi)) *
...      np.exp(-(x - loc)**2 / (2 * scale**2)))
>>> plt.plot(x,g)

НазадОткрыть во вкладке